SQ Lower Bounds for Non-Gaussian Component Analysis with Weaker Assumptions

We study the complexity of Non-Gaussian Component Analysis (NGCA) in the Statistical Query (SQ) model. Prior work developed a general methodology to prove SQ lower bounds for this task that have been applicable to a wide range of contexts. In particular, it was known that for any univariate distribution $A$ satisfying certain conditions, distinguishing between a standard multivariate Gaussian and a distribution that behaves like $A$ in a random hidden direction and like a standard Gaussian in the orthogonal complement, is SQ-hard. The required conditions were that (1) $A$ matches many low-order moments with the standard univariate Gaussian, and (2) the chi-squared norm of $A$ with respect to the standard Gaussian is finite. While the moment-matching condition is necessary for hardness, the chi-squared condition was only required for technical reasons. In this work, we establish that the latter condition is indeed not necessary. In particular, we prove near-optimal SQ lower bounds for NGCA under the moment-matching condition only. Our result naturally generalizes to the setting of a hidden subspace. Leveraging our general SQ lower bound, we obtain near-optimal SQ lower bounds for a range of concrete estimation tasks where existing techniques provide sub-optimal or even vacuous guarantees.

SQ Lower Bounds for Learning Mixtures of Linear Classifiers

We study the problem of learning mixtures of linear classifiers under Gaussian covariates. Given sample access to a mixture of $r$ distributions on $\mathbb{R}^n$ of the form $(\mathbf{x},y_{\ell})$, $\ell\in [r]$, where $\mathbf{x}\sim\mathcal{N}(0,\mathbf{I}_n)$ and $y_\ell=\mathrm{sign}(\langle\mathbf{v}_\ell,\mathbf{x}\rangle)$ for an unknown unit vector $\mathbf{v}_\ell$, the goal is to learn the underlying distribution in total variation distance. Our main result is a Statistical Query (SQ) lower bound suggesting that known algorithms for this problem are essentially best possible, even for the special case of uniform mixtures. In particular, we show that the complexity of any SQ algorithm for the problem is $n^{\mathrm{poly}(1/\Delta) \log(r)}$, where $\Delta$ is a lower bound on the pairwise $\ell_2$-separation between the $\mathbf{v}_\ell$'s. The key technical ingredient underlying our result is a new construction of spherical designs that may be of independent interest.

StEik: Stabilizing the Optimization of Neural Signed Distance Functions and Finer Shape Representation

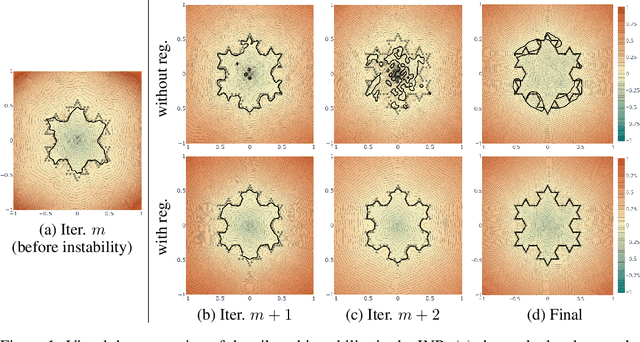
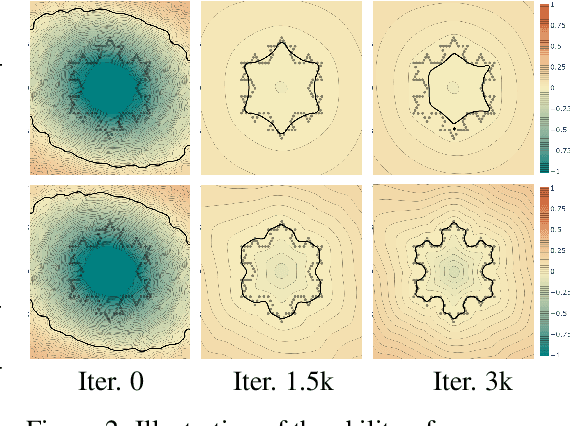
We present new insights and a novel paradigm (StEik) for learning implicit neural representations (INR) of shapes. In particular, we shed light on the popular eikonal loss used for imposing a signed distance function constraint in INR. We show analytically that as the representation power of the network increases, the optimization approaches a partial differential equation (PDE) in the continuum limit that is unstable. We show that this instability can manifest in existing network optimization, leading to irregularities in the reconstructed surface and/or convergence to sub-optimal local minima, and thus fails to capture fine geometric and topological structure. We show analytically how other terms added to the loss, currently used in the literature for other purposes, can actually eliminate these instabilities. However, such terms can over-regularize the surface, preventing the representation of fine shape detail. Based on a similar PDE theory for the continuum limit, we introduce a new regularization term that still counteracts the eikonal instability but without over-regularizing. Furthermore, since stability is now guaranteed in the continuum limit, this stabilization also allows for considering new network structures that are able to represent finer shape detail. We introduce such a structure based on quadratic layers. Experiments on multiple benchmark data sets show that our new regularization and network are able to capture more precise shape details and more accurate topology than existing state-of-the-art.

SQ Lower Bounds for Learning Single Neurons with Massart Noise

We study the problem of PAC learning a single neuron in the presence of Massart noise. Specifically, for a known activation function $f: \mathbb{R} \to \mathbb{R}$, the learner is given access to labeled examples $(\mathbf{x}, y) \in \mathbb{R}^d \times \mathbb{R}$, where the marginal distribution of $\mathbf{x}$ is arbitrary and the corresponding label $y$ is a Massart corruption of $f(\langle \mathbf{w}, \mathbf{x} \rangle)$. The goal of the learner is to output a hypothesis $h: \mathbb{R}^d \to \mathbb{R}$ with small squared loss. For a range of activation functions, including ReLUs, we establish super-polynomial Statistical Query (SQ) lower bounds for this learning problem. In more detail, we prove that no efficient SQ algorithm can approximate the optimal error within any constant factor. Our main technical contribution is a novel SQ-hard construction for learning $\{ \pm 1\}$-weight Massart halfspaces on the Boolean hypercube that is interesting on its own right.

Optimal SQ Lower Bounds for Robustly Learning Discrete Product Distributions and Ising Models

We establish optimal Statistical Query (SQ) lower bounds for robustly learning certain families of discrete high-dimensional distributions. In particular, we show that no efficient SQ algorithm with access to an $\epsilon$-corrupted binary product distribution can learn its mean within $\ell_2$-error $o(\epsilon \sqrt{\log(1/\epsilon)})$. Similarly, we show that no efficient SQ algorithm with access to an $\epsilon$-corrupted ferromagnetic high-temperature Ising model can learn the model to total variation distance $o(\epsilon \log(1/\epsilon))$. Our SQ lower bounds match the error guarantees of known algorithms for these problems, providing evidence that current upper bounds for these tasks are best possible. At the technical level, we develop a generic SQ lower bound for discrete high-dimensional distributions starting from low dimensional moment matching constructions that we believe will find other applications. Additionally, we introduce new ideas to analyze these moment-matching constructions for discrete univariate distributions.

Outlier-Robust Learning of Ising Models Under Dobrushin's Condition

We study the problem of learning Ising models satisfying Dobrushin's condition in the outlier-robust setting where a constant fraction of the samples are adversarially corrupted. Our main result is to provide the first computationally efficient robust learning algorithm for this problem with near-optimal error guarantees. Our algorithm can be seen as a special case of an algorithm for robustly learning a distribution from a general exponential family. To prove its correctness for Ising models, we establish new anti-concentration results for degree-$2$ polynomials of Ising models that may be of independent interest.

Correlated Feature Selection with Extended Exclusive Group Lasso

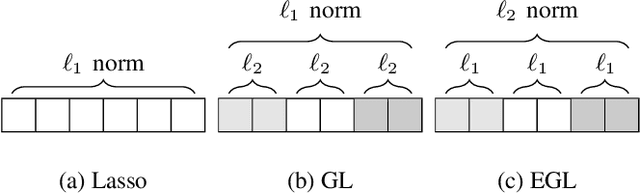
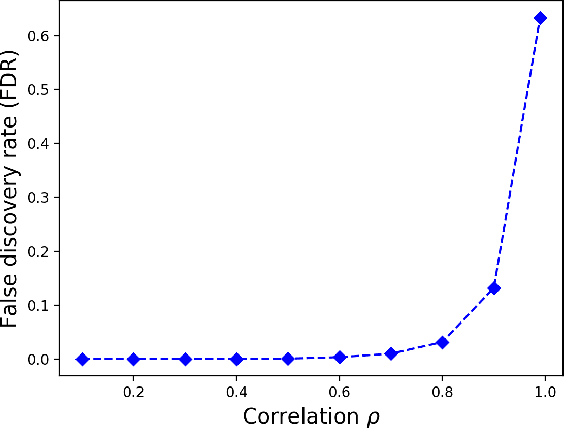
In many high dimensional classification or regression problems set in a biological context, the complete identification of the set of informative features is often as important as predictive accuracy, since this can provide mechanistic insight and conceptual understanding. Lasso and related algorithms have been widely used since their sparse solutions naturally identify a set of informative features. However, Lasso performs erratically when features are correlated. This limits the use of such algorithms in biological problems, where features such as genes often work together in pathways, leading to sets of highly correlated features. In this paper, we examine the performance of a Lasso derivative, the exclusive group Lasso, in this setting. We propose fast algorithms to solve the exclusive group Lasso, and introduce a solution to the case when the underlying group structure is unknown. The solution combines stability selection with random group allocation and introduction of artificial features. Experiments with both synthetic and real-world data highlight the advantages of this proposed methodology over Lasso in comprehensive selection of informative features.

Attribute-Guided Network for Cross-Modal Zero-Shot Hashing

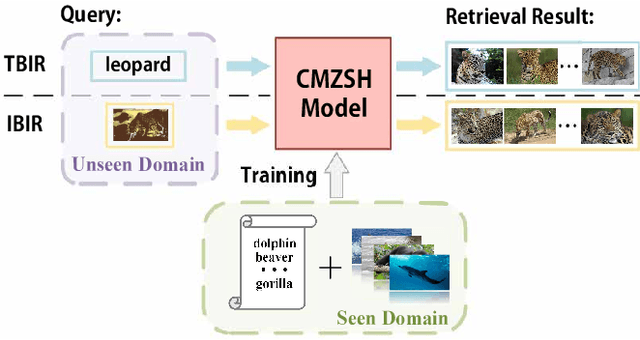
Zero-Shot Hashing aims at learning a hashing model that is trained only by instances from seen categories but can generate well to those of unseen categories. Typically, it is achieved by utilizing a semantic embedding space to transfer knowledge from seen domain to unseen domain. Existing efforts mainly focus on single-modal retrieval task, especially Image-Based Image Retrieval (IBIR). However, as a highlighted research topic in the field of hashing, cross-modal retrieval is more common in real world applications. To address the Cross-Modal Zero-Shot Hashing (CMZSH) retrieval task, we propose a novel Attribute-Guided Network (AgNet), which can perform not only IBIR, but also Text-Based Image Retrieval (TBIR). In particular, AgNet aligns different modal data into a semantically rich attribute space, which bridges the gap caused by modality heterogeneity and zero-shot setting. We also design an effective strategy that exploits the attribute to guide the generation of hash codes for image and text within the same network. Extensive experimental results on three benchmark datasets (AwA, SUN, and ImageNet) demonstrate the superiority of AgNet on both cross-modal and single-modal zero-shot image retrieval tasks.