Deep Learning for Crack Detection: A Review of Learning Paradigms, Generalizability, and Datasets

Crack detection plays a crucial role in civil infrastructures, including inspection of pavements, buildings, etc., and deep learning has significantly advanced this field in recent years. While numerous technical and review papers exist in this domain, emerging trends are reshaping the landscape. These shifts include transitions in learning paradigms (from fully supervised learning to semi-supervised, weakly-supervised, unsupervised, few-shot, domain adaptation and fine-tuning foundation models), improvements in generalizability (from single-dataset performance to cross-dataset evaluation), and diversification in dataset reacquisition (from RGB images to specialized sensor-based data). In this review, we systematically analyze these trends and highlight representative works. Additionally, we introduce a new dataset collected with 3D laser scans, 3DCrack, to support future research and conduct extensive benchmarking experiments to establish baselines for commonly used deep learning methodologies, including recent foundation models. Our findings provide insights into the evolving methodologies and future directions in deep learning-based crack detection. Project page: https://github.com/nantonzhang/Awesome-Crack-Detection

EscherNet++: Simultaneous Amodal Completion and Scalable View Synthesis through Masked Fine-Tuning and Enhanced Feed-Forward 3D Reconstruction

We propose EscherNet++, a masked fine-tuned diffusion model that can synthesize novel views of objects in a zero-shot manner with amodal completion ability. Existing approaches utilize multiple stages and complex pipelines to first hallucinate missing parts of the image and then perform novel view synthesis, which fail to consider cross-view dependencies and require redundant storage and computing for separate stages. Instead, we apply masked fine-tuning including input-level and feature-level masking to enable an end-to-end model with the improved ability to synthesize novel views and conduct amodal completion. In addition, we empirically integrate our model with other feed-forward image-to-mesh models without extra training and achieve competitive results with reconstruction time decreased by 95%, thanks to its ability to synthesize arbitrary query views. Our method's scalable nature further enhances fast 3D reconstruction. Despite fine-tuning on a smaller dataset and batch size, our method achieves state-of-the-art results, improving PSNR by 3.9 and Volume IoU by 0.28 on occluded tasks in 10-input settings, while also generalizing to real-world occluded reconstruction.

Event-Based Eye Tracking. AIS 2024 Challenge Survey

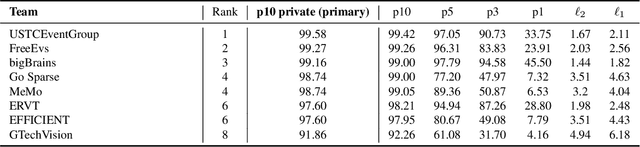
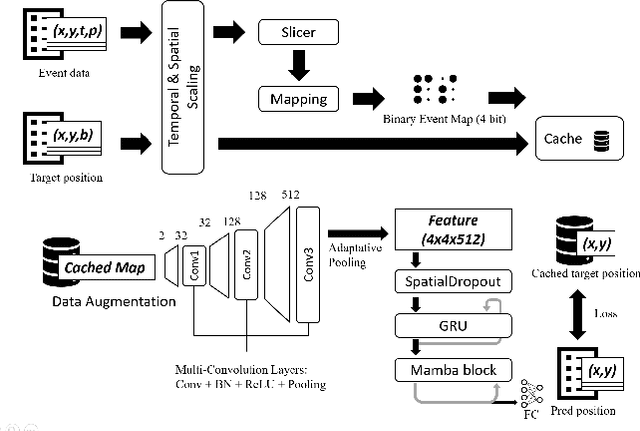
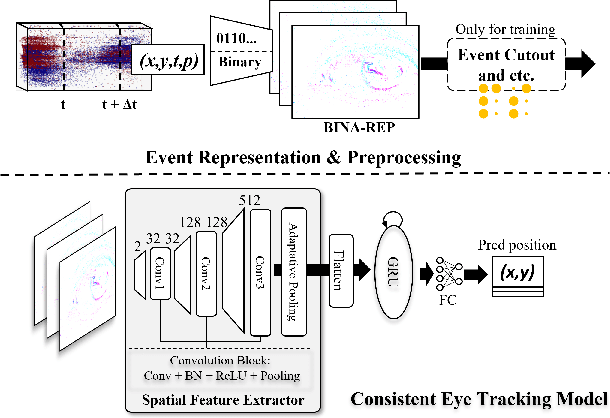
This survey reviews the AIS 2024 Event-Based Eye Tracking (EET) Challenge. The task of the challenge focuses on processing eye movement recorded with event cameras and predicting the pupil center of the eye. The challenge emphasizes efficient eye tracking with event cameras to achieve good task accuracy and efficiency trade-off. During the challenge period, 38 participants registered for the Kaggle competition, and 8 teams submitted a challenge factsheet. The novel and diverse methods from the submitted factsheets are reviewed and analyzed in this survey to advance future event-based eye tracking research.

StEik: Stabilizing the Optimization of Neural Signed Distance Functions and Finer Shape Representation

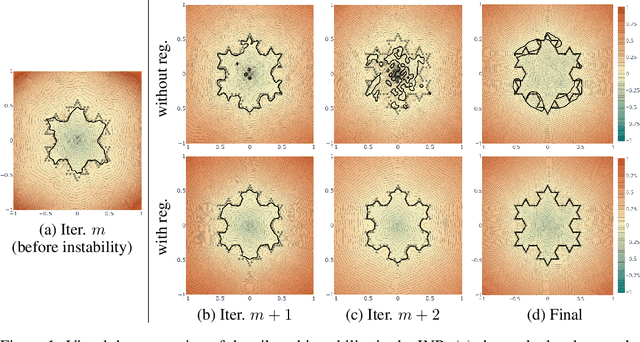
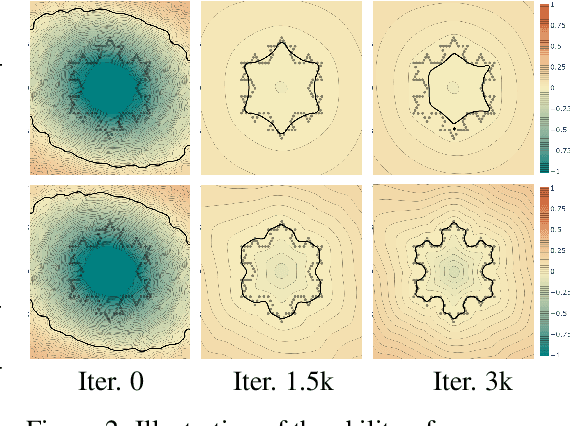
We present new insights and a novel paradigm (StEik) for learning implicit neural representations (INR) of shapes. In particular, we shed light on the popular eikonal loss used for imposing a signed distance function constraint in INR. We show analytically that as the representation power of the network increases, the optimization approaches a partial differential equation (PDE) in the continuum limit that is unstable. We show that this instability can manifest in existing network optimization, leading to irregularities in the reconstructed surface and/or convergence to sub-optimal local minima, and thus fails to capture fine geometric and topological structure. We show analytically how other terms added to the loss, currently used in the literature for other purposes, can actually eliminate these instabilities. However, such terms can over-regularize the surface, preventing the representation of fine shape detail. Based on a similar PDE theory for the continuum limit, we introduce a new regularization term that still counteracts the eikonal instability but without over-regularizing. Furthermore, since stability is now guaranteed in the continuum limit, this stabilization also allows for considering new network structures that are able to represent finer shape detail. We introduce such a structure based on quadratic layers. Experiments on multiple benchmark data sets show that our new regularization and network are able to capture more precise shape details and more accurate topology than existing state-of-the-art.

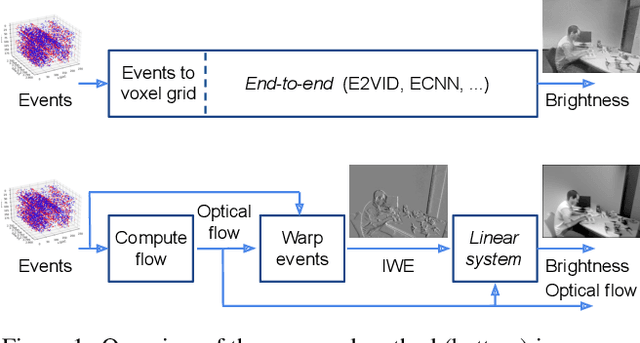
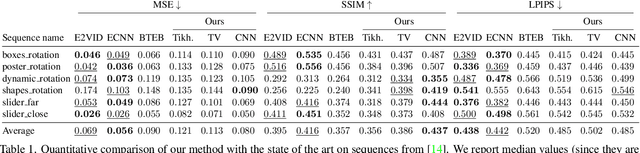
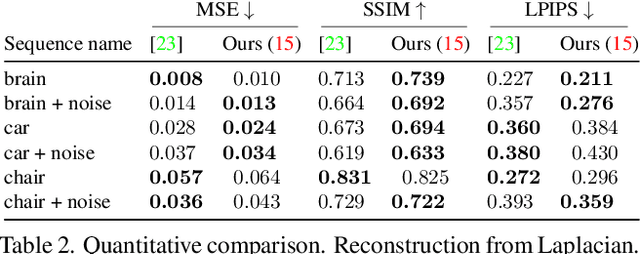
Image Reconstruction from Events. Why learn it?

Traditional cameras measure image intensity. Event cameras, by contrast, measure per-pixel temporal intensity changes asynchronously. Recovering intensity from events is a popular research topic since the reconstructed images inherit the high dynamic range (HDR) and high-speed properties of events; hence they can be used in many robotic vision applications and to generate slow-motion HDR videos. However, state-of-the-art methods tackle this problem by training an event-to-image recurrent neural network (RNN), which lacks explainability and is difficult to tune. In this work we show, for the first time, how tackling the joint problem of motion and intensity estimation leads us to model event-based image reconstruction as a linear inverse problem that can be solved without training an image reconstruction RNN. Instead, classical and learning-based image priors can be used to solve the problem and remove artifacts from the reconstructed images. The experiments show that the proposed approach generates images with visual quality on par with state-of-the-art methods despite only using data from a short time interval (i.e., without recurrent connections). Our method can also be used to improve the quality of images reconstructed by approaches that first estimate the image Laplacian; here our method can be interpreted as Poisson reconstruction guided by image priors.

Deep Learning 3D Dose Prediction for Conventional Lung IMRT Using Consistent/Unbiased Automated Plans

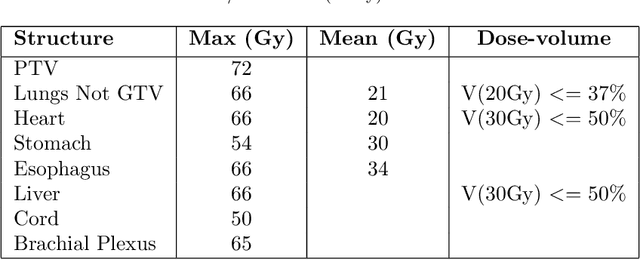
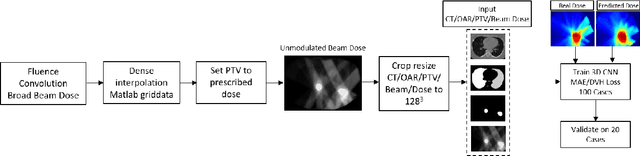
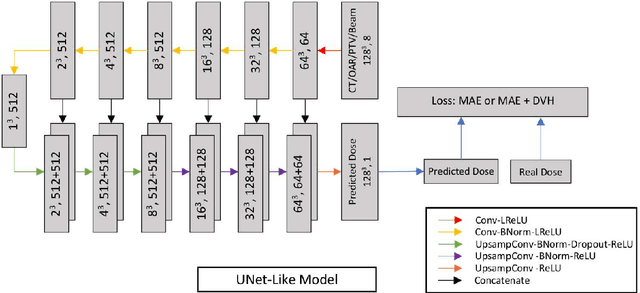
Deep learning (DL) 3D dose prediction has recently gained a lot of attention. However, the variability of plan quality in the training dataset, generated manually by planners with wide range of expertise, can dramatically effect the quality of the final predictions. Moreover, any changes in the clinical criteria requires a new set of manually generated plans by planners to build a new prediction model. In this work, we instead use consistent plans generated by our in-house automated planning system (named ``ECHO'') to train the DL model. ECHO (expedited constrained hierarchical optimization) generates consistent/unbiased plans by solving large-scale constrained optimization problems sequentially. If the clinical criteria changes, a new training data set can be easily generated offline using ECHO, with no or limited human intervention, making the DL-based prediction model easily adaptable to the changes in the clinical practice. We used 120 conventional lung patients (100 for training, 20 for testing) with different beam configurations and trained our DL-model using manually-generated as well as automated ECHO plans. We evaluated different inputs: (1) CT+(PTV/OAR)contours, and (2) CT+contours+beam configurations, and different loss functions: (1) MAE (mean absolute error), and (2) MAE+DVH (dose volume histograms). The quality of the predictions was compared using different DVH metrics as well as dose-score and DVH-score, recently introduced by the AAPM knowledge-based planning grand challenge. The best results were obtained using automated ECHO plans and CT+contours+beam as training inputs and MAE+DVH as loss function.

An Efficiently Coupled Shape and Appearance Prior for Active Contour Segmentation

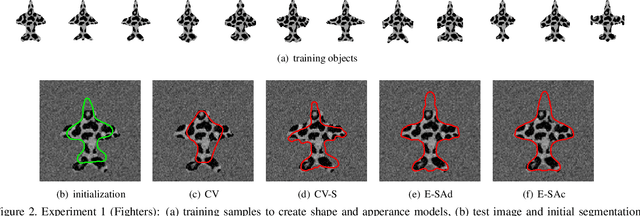
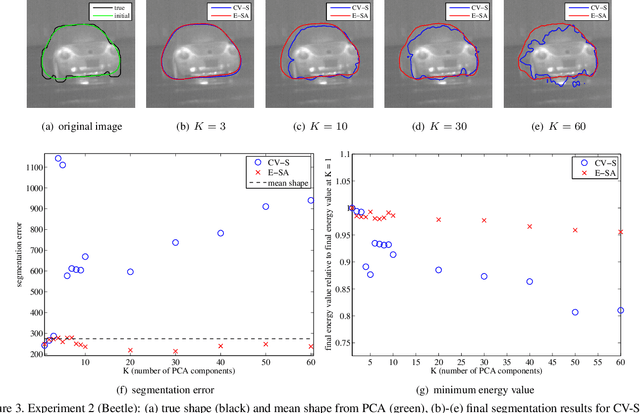
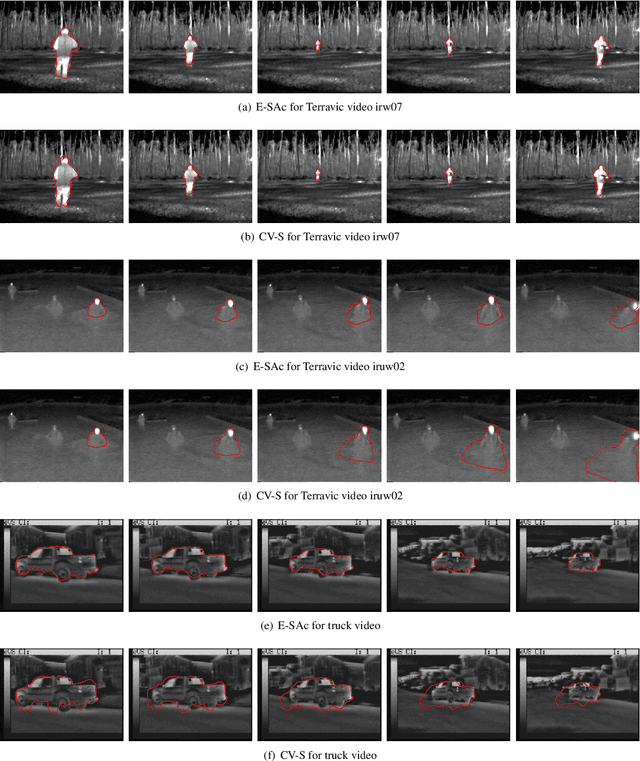
This paper proposes a novel training model based on shape and appearance features for object segmentation in images and videos. Whereas most such models rely on two-dimensional appearance templates or a finite set of descriptors, our appearance-based feature is a one-dimensional function, which is efficiently coupled with the object's shape by integrating intensities along the object's iso-contours. Joint PCA training on these shape and appearance features further exploits shape-appearance correlations and the resulting training model is incorporated in an active-contour-type energy functional for recognition-segmentation tasks. Experiments on synthetic and infrared images demonstrate how this shape and appearance training model improves accuracy compared to methods based on the Chan-Vese energy.

Multitask 3D CBCT-to-CT Translation and Organs-at-Risk Segmentation Using Physics-Based Data Augmentation

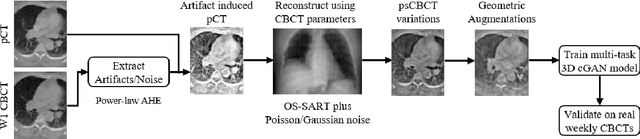
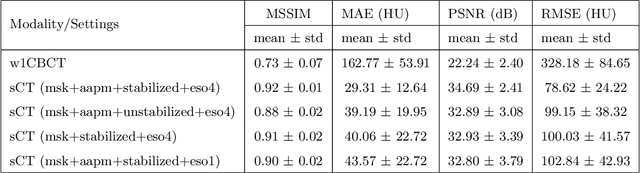
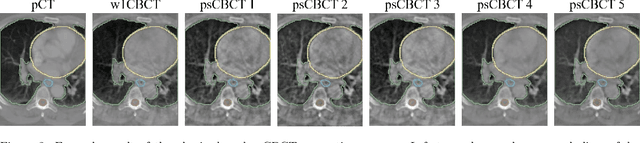
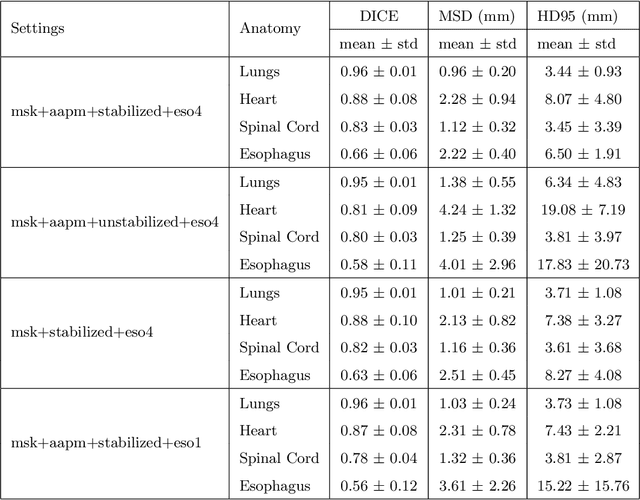
Purpose: In current clinical practice, noisy and artifact-ridden weekly cone-beam computed tomography (CBCT) images are only used for patient setup during radiotherapy. Treatment planning is done once at the beginning of the treatment using high-quality planning CT (pCT) images and manual contours for organs-at-risk (OARs) structures. If the quality of the weekly CBCT images can be improved while simultaneously segmenting OAR structures, this can provide critical information for adapting radiotherapy mid-treatment as well as for deriving biomarkers for treatment response. Methods: Using a novel physics-based data augmentation strategy, we synthesize a large dataset of perfectly/inherently registered planning CT and synthetic-CBCT pairs for locally advanced lung cancer patient cohort, which are then used in a multitask 3D deep learning framework to simultaneously segment and translate real weekly CBCT images to high-quality planning CT-like images. Results: We compared the synthetic CT and OAR segmentations generated by the model to real planning CT and manual OAR segmentations and showed promising results. The real week 1 (baseline) CBCT images which had an average MAE of 162.77 HU compared to pCT images are translated to synthetic CT images that exhibit a drastically improved average MAE of 29.31 HU and average structural similarity of 92% with the pCT images. The average DICE scores of the 3D organs-at-risk segmentations are: lungs 0.96, heart 0.88, spinal cord 0.83 and esophagus 0.66. Conclusions: We demonstrate an approach to translate artifact-ridden CBCT images to high quality synthetic CT images while simultaneously generating good quality segmentation masks for different organs-at-risk. This approach could allow clinicians to adjust treatment plans using only the routine low-quality CBCT images, potentially improving patient outcomes.

Verifying the Causes of Adversarial Examples

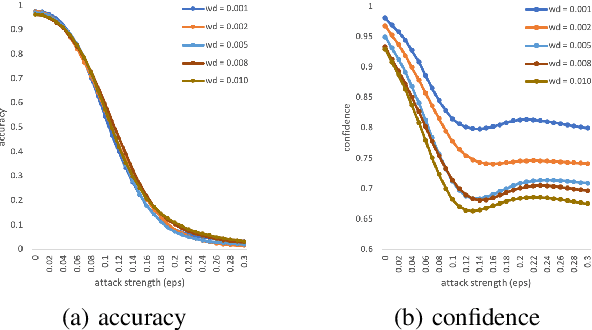
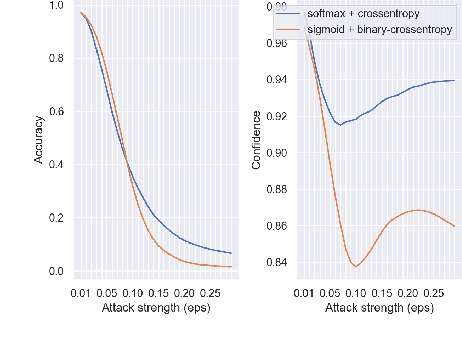
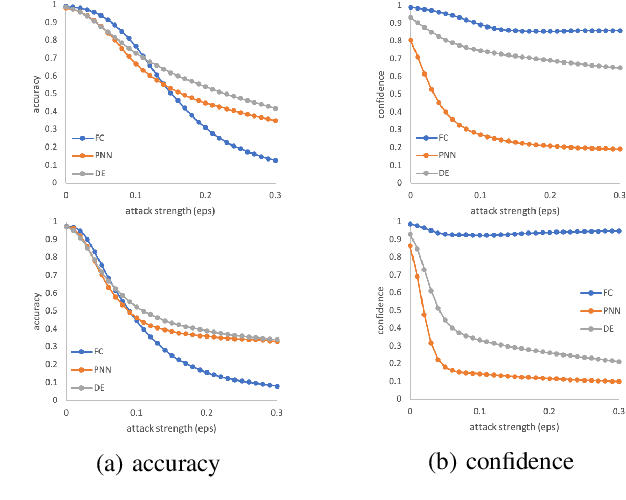
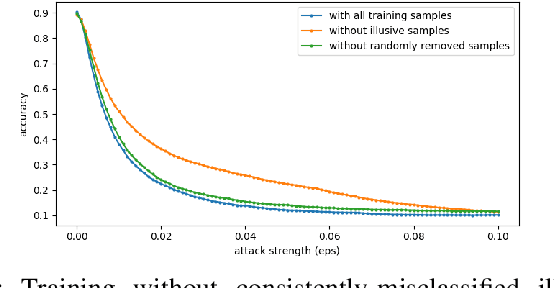
The robustness of neural networks is challenged by adversarial examples that contain almost imperceptible perturbations to inputs, which mislead a classifier to incorrect outputs in high confidence. Limited by the extreme difficulty in examining a high-dimensional image space thoroughly, research on explaining and justifying the causes of adversarial examples falls behind studies on attacks and defenses. In this paper, we present a collection of potential causes of adversarial examples and verify (or partially verify) them through carefully-designed controlled experiments. The major causes of adversarial examples include model linearity, one-sum constraint, and geometry of the categories. To control the effect of those causes, multiple techniques are applied such as $L_2$ normalization, replacement of loss functions, construction of reference datasets, and novel models using multi-layer perceptron probabilistic neural networks (MLP-PNN) and density estimation (DE). Our experiment results show that geometric factors tend to be more direct causes and statistical factors magnify the phenomenon, especially for assigning high prediction confidence. We believe this paper will inspire more studies to rigorously investigate the root causes of adversarial examples, which in turn provide useful guidance on designing more robust models.

An Adaptive View of Adversarial Robustness from Test-time Smoothing Defense

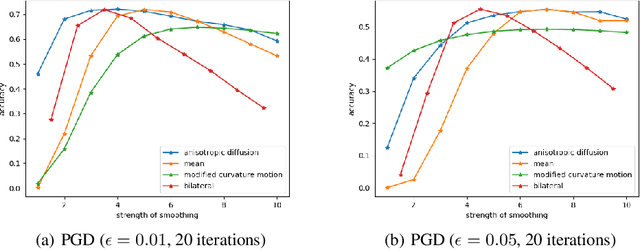
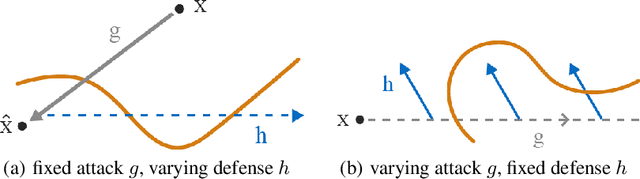
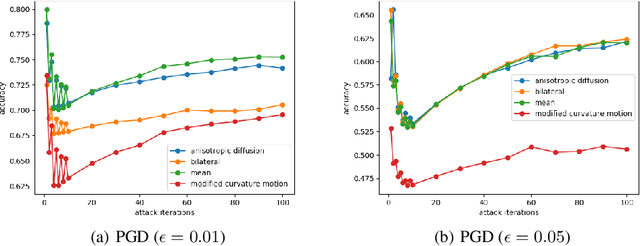
The safety and robustness of learning-based decision-making systems are under threats from adversarial examples, as imperceptible perturbations can mislead neural networks to completely different outputs. In this paper, we present an adaptive view of the issue via evaluating various test-time smoothing defense against white-box untargeted adversarial examples. Through controlled experiments with pretrained ResNet-152 on ImageNet, we first illustrate the non-monotonic relation between adversarial attacks and smoothing defenses. Then at the dataset level, we observe large variance among samples and show that it is easy to inflate accuracy (even to 100%) or build large-scale (i.e., with size ~10^4) subsets on which a designated method outperforms others by a large margin. Finally at the sample level, as different adversarial examples require different degrees of defense, the potential advantages of iterative methods are also discussed. We hope this paper reveal useful behaviors of test-time defenses, which could help improve the evaluation process for adversarial robustness in the future.