Optimal Parallelization of Boosting

Recent works on the parallel complexity of Boosting have established strong lower bounds on the tradeoff between the number of training rounds $p$ and the total parallel work per round $t$. These works have also presented highly non-trivial parallel algorithms that shed light on different regions of this tradeoff. Despite these advancements, a significant gap persists between the theoretical lower bounds and the performance of these algorithms across much of the tradeoff space. In this work, we essentially close this gap by providing both improved lower bounds on the parallel complexity of weak-to-strong learners, and a parallel Boosting algorithm whose performance matches these bounds across the entire $p$ vs.~$t$ compromise spectrum, up to logarithmic factors. Ultimately, this work settles the true parallel complexity of Boosting algorithms that are nearly sample-optimal.

Boosting, Voting Classifiers and Randomized Sample Compression Schemes

In boosting, we aim to leverage multiple weak learners to produce a strong learner. At the center of this paradigm lies the concept of building the strong learner as a voting classifier, which outputs a weighted majority vote of the weak learners. While many successful boosting algorithms, such as the iconic AdaBoost, produce voting classifiers, their theoretical performance has long remained sub-optimal: the best known bounds on the number of training examples necessary for a voting classifier to obtain a given accuracy has so far always contained at least two logarithmic factors above what is known to be achievable by general weak-to-strong learners. In this work, we break this barrier by proposing a randomized boosting algorithm that outputs voting classifiers whose generalization error contains a single logarithmic dependency on the sample size. We obtain this result by building a general framework that extends sample compression methods to support randomized learning algorithms based on sub-sampling.

Polynomially Over-Parameterized Convolutional Neural Networks Contain Structured Strong Winning Lottery Tickets

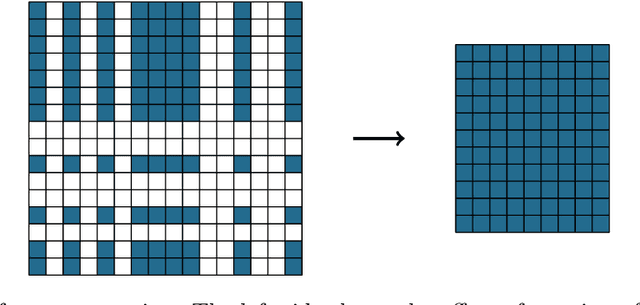
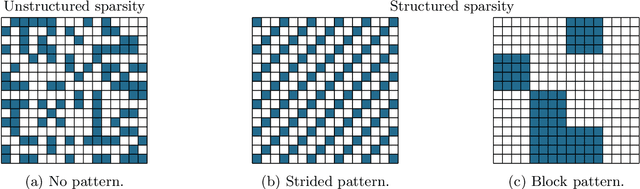
The Strong Lottery Ticket Hypothesis (SLTH) states that randomly-initialised neural networks likely contain subnetworks that perform well without any training. Although unstructured pruning has been extensively studied in this context, its structured counterpart, which can deliver significant computational and memory efficiency gains, has been largely unexplored. One of the main reasons for this gap is the limitations of the underlying mathematical tools used in formal analyses of the SLTH. In this paper, we overcome these limitations: we leverage recent advances in the multidimensional generalisation of the Random Subset-Sum Problem and obtain a variant that admits the stochastic dependencies that arise when addressing structured pruning in the SLTH. We apply this result to prove, for a wide class of random Convolutional Neural Networks, the existence of structured subnetworks that can approximate any sufficiently smaller network. This result provides the first sub-exponential bound around the SLTH for structured pruning, opening up new avenues for further research on the hypothesis and contributing to the understanding of the role of over-parameterization in deep learning.