Polynomially Over-Parameterized Convolutional Neural Networks Contain Structured Strong Winning Lottery Tickets
Paper and Code
Nov 16, 2023
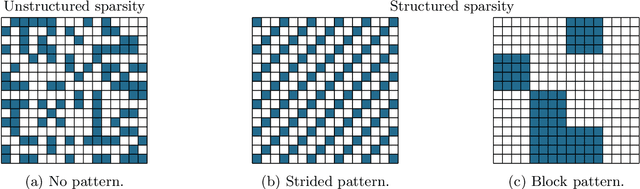
The Strong Lottery Ticket Hypothesis (SLTH) states that randomly-initialised neural networks likely contain subnetworks that perform well without any training. Although unstructured pruning has been extensively studied in this context, its structured counterpart, which can deliver significant computational and memory efficiency gains, has been largely unexplored. One of the main reasons for this gap is the limitations of the underlying mathematical tools used in formal analyses of the SLTH. In this paper, we overcome these limitations: we leverage recent advances in the multidimensional generalisation of the Random Subset-Sum Problem and obtain a variant that admits the stochastic dependencies that arise when addressing structured pruning in the SLTH. We apply this result to prove, for a wide class of random Convolutional Neural Networks, the existence of structured subnetworks that can approximate any sufficiently smaller network. This result provides the first sub-exponential bound around the SLTH for structured pruning, opening up new avenues for further research on the hypothesis and contributing to the understanding of the role of over-parameterization in deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge