On the Sparsity of the Strong Lottery Ticket Hypothesis

Considerable research efforts have recently been made to show that a random neural network $N$ contains subnetworks capable of accurately approximating any given neural network that is sufficiently smaller than $N$, without any training. This line of research, known as the Strong Lottery Ticket Hypothesis (SLTH), was originally motivated by the weaker Lottery Ticket Hypothesis, which states that a sufficiently large random neural network $N$ contains \emph{sparse} subnetworks that can be trained efficiently to achieve performance comparable to that of training the entire network $N$. Despite its original motivation, results on the SLTH have so far not provided any guarantee on the size of subnetworks. Such limitation is due to the nature of the main technical tool leveraged by these results, the Random Subset Sum (RSS) Problem. Informally, the RSS Problem asks how large a random i.i.d. sample $\Omega$ should be so that we are able to approximate any number in $[-1,1]$, up to an error of $ \epsilon$, as the sum of a suitable subset of $\Omega$. We provide the first proof of the SLTH in classical settings, such as dense and equivariant networks, with guarantees on the sparsity of the subnetworks. Central to our results, is the proof of an essentially tight bound on the Random Fixed-Size Subset Sum Problem (RFSS), a variant of the RSS Problem in which we only ask for subsets of a given size, which is of independent interest.

Polynomially Over-Parameterized Convolutional Neural Networks Contain Structured Strong Winning Lottery Tickets

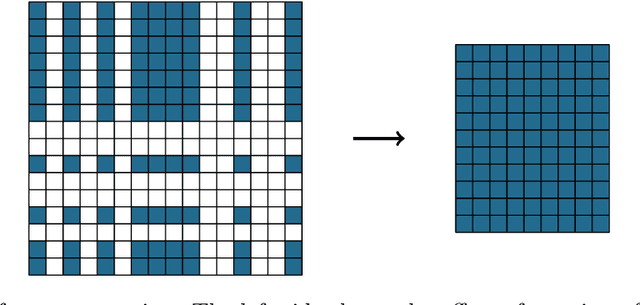
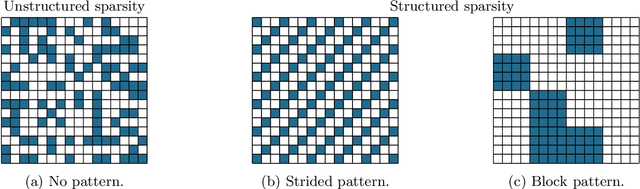
The Strong Lottery Ticket Hypothesis (SLTH) states that randomly-initialised neural networks likely contain subnetworks that perform well without any training. Although unstructured pruning has been extensively studied in this context, its structured counterpart, which can deliver significant computational and memory efficiency gains, has been largely unexplored. One of the main reasons for this gap is the limitations of the underlying mathematical tools used in formal analyses of the SLTH. In this paper, we overcome these limitations: we leverage recent advances in the multidimensional generalisation of the Random Subset-Sum Problem and obtain a variant that admits the stochastic dependencies that arise when addressing structured pruning in the SLTH. We apply this result to prove, for a wide class of random Convolutional Neural Networks, the existence of structured subnetworks that can approximate any sufficiently smaller network. This result provides the first sub-exponential bound around the SLTH for structured pruning, opening up new avenues for further research on the hypothesis and contributing to the understanding of the role of over-parameterization in deep learning.

On the Multidimensional Random Subset Sum Problem

In the Random Subset Sum Problem, given $n$ i.i.d. random variables $X_1, ..., X_n$, we wish to approximate any point $z \in [-1,1]$ as the sum of a suitable subset $X_{i_1(z)}, ..., X_{i_s(z)}$ of them, up to error $\varepsilon$. Despite its simple statement, this problem is of fundamental interest to both theoretical computer science and statistical mechanics. More recently, it gained renewed attention for its implications in the theory of Artificial Neural Networks. An obvious multidimensional generalisation of the problem is to consider $n$ i.i.d.\ $d$-dimensional random vectors, with the objective of approximating every point $\mathbf{z} \in [-1,1]^d$. Rather surprisingly, after Lueker's 1998 proof that, in the one-dimensional setting, $n=O(\log \frac 1\varepsilon)$ samples guarantee the approximation property with high probability, little progress has been made on achieving the above generalisation. In this work, we prove that, in $d$ dimensions, $n = O(d^3\log \frac 1\varepsilon \cdot (\log \frac 1\varepsilon + \log d))$ samples suffice for the approximation property to hold with high probability. As an application highlighting the potential interest of this result, we prove that a recently proposed neural network model exhibits \emph{universality}: with high probability, the model can approximate any neural network within a polynomial overhead in the number of parameters.

Planning with Biological Neurons and Synapses

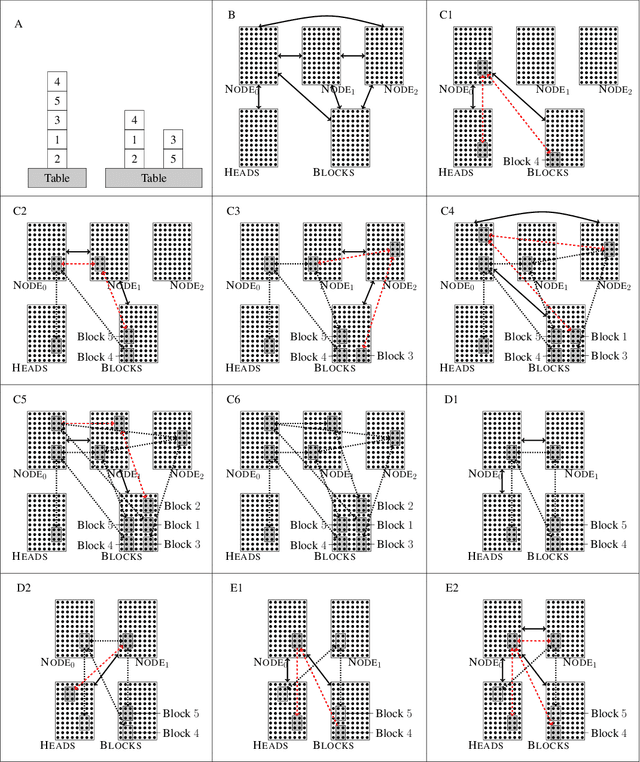
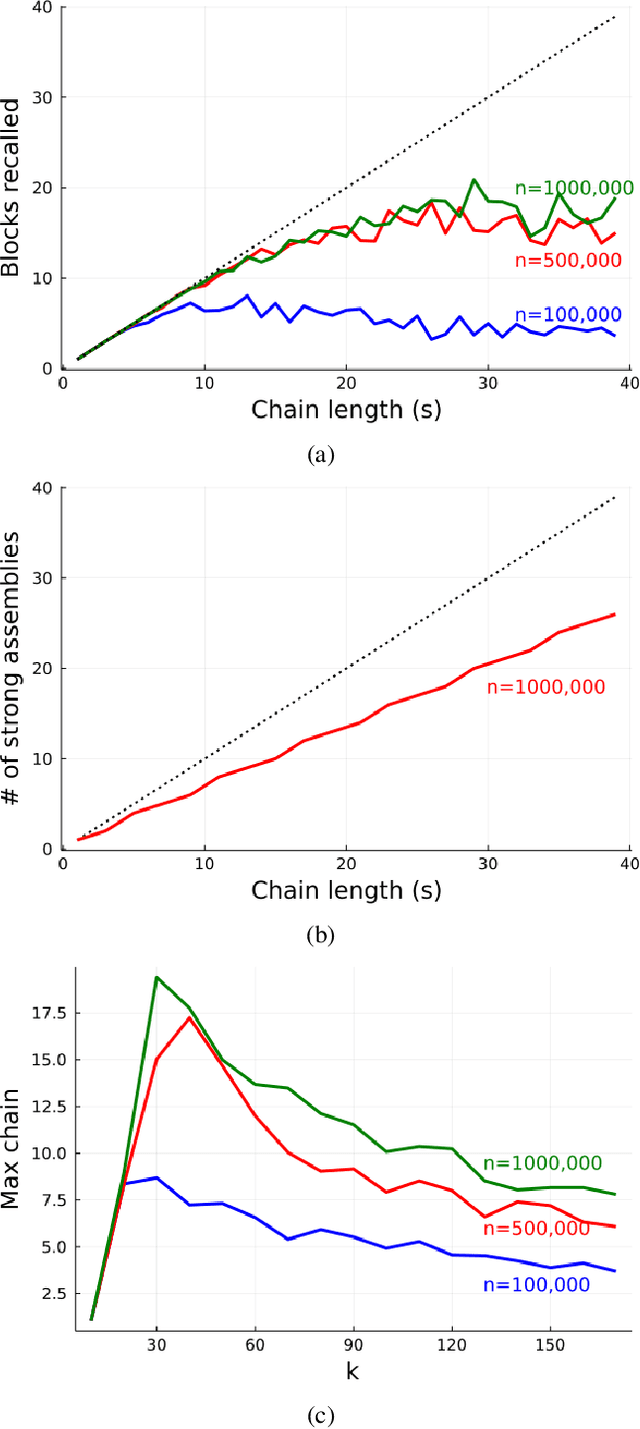
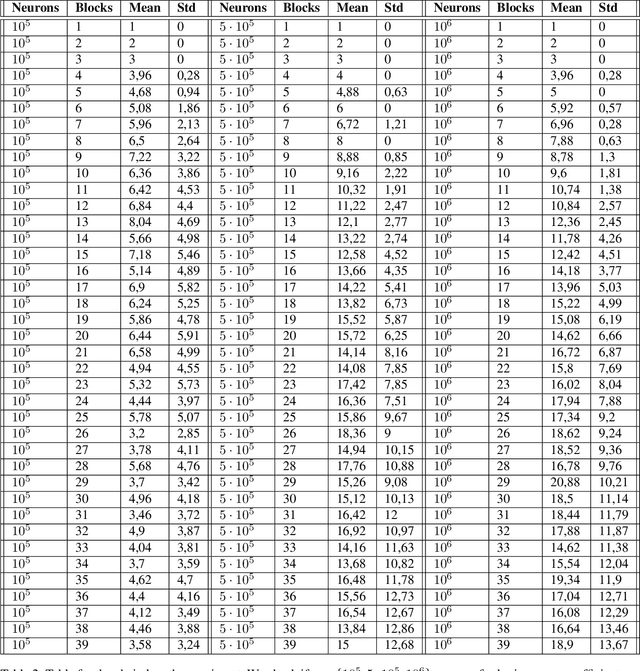
We revisit the planning problem in the blocks world, and we implement a known heuristic for this task. Importantly, our implementation is biologically plausible, in the sense that it is carried out exclusively through the spiking of neurons. Even though much has been accomplished in the blocks world over the past five decades, we believe that this is the first algorithm of its kind. The input is a sequence of symbols encoding an initial set of block stacks as well as a target set, and the output is a sequence of motion commands such as "put the top block in stack 1 on the table". The program is written in the Assembly Calculus, a recently proposed computational framework meant to model computation in the brain by bridging the gap between neural activity and cognitive function. Its elementary objects are assemblies of neurons (stable sets of neurons whose simultaneous firing signifies that the subject is thinking of an object, concept, word, etc.), its commands include project and merge, and its execution model is based on widely accepted tenets of neuroscience. A program in this framework essentially sets up a dynamical system of neurons and synapses that eventually, with high probability, accomplishes the task. The purpose of this work is to establish empirically that reasonably large programs in the Assembly Calculus can execute correctly and reliably; and that rather realistic -- if idealized -- higher cognitive functions, such as planning in the blocks world, can be implemented successfully by such programs.

A Comparative Study of Neural Network Compression

There has recently been an increasing desire to evaluate neural networks locally on computationally-limited devices in order to exploit their recent effectiveness for several applications; such effectiveness has nevertheless come together with a considerable increase in the size of modern neural networks, which constitute a major downside in several of the aforementioned computationally-limited settings. There has thus been a demand of compression techniques for neural networks. Several proposal in this direction have been made, which famously include hashing-based methods and pruning-based ones. However, the evaluation of the efficacy of these techniques has so far been heterogeneous, with no clear evidence in favor of any of them over the others. The goal of this work is to address this latter issue by providing a comparative study. While most previous studies test the capability of a technique in reducing the number of parameters of state-of-the-art networks , we follow [CWT + 15] in evaluating their performance on basic ar-chitectures on the MNIST dataset and variants of it, which allows for a clearer analysis of some aspects of their behavior. To the best of our knowledge, we are the first to directly compare famous approaches such as HashedNet, Optimal Brain Damage (OBD), and magnitude-based pruning with L1 and L2 regularization among them and against equivalent-size feed-forward neural networks with simple (fully-connected) and structural (convolutional) neural networks. Rather surprisingly, our experiments show that (iterative) pruning-based methods are substantially better than the HashedNet architecture, whose compression doesn't appear advantageous to a carefully chosen convolutional network. We also show that, when the compression level is high, the famous OBD pruning heuristics deteriorates to the point of being less efficient than simple magnitude-based techniques.