Trading-off Accuracy and Communication Cost in Federated Learning

Leveraging the training-by-pruning paradigm introduced by Zhou et al. and Isik et al. introduced a federated learning protocol that achieves a 34-fold reduction in communication cost. We achieve a compression improvements of orders of orders of magnitude over the state-of-the-art. The central idea of our framework is to encode the network weights $\vec w$ by a the vector of trainable parameters $\vec p$, such that $\vec w = Q\cdot \vec p$ where $Q$ is a carefully-generate sparse random matrix (that remains fixed throughout training). In such framework, the previous work of Zhou et al. [NeurIPS'19] is retrieved when $Q$ is diagonal and $\vec p$ has the same dimension of $\vec w$. We instead show that $\vec p$ can effectively be chosen much smaller than $\vec w$, while retaining the same accuracy at the price of a decrease of the sparsity of $Q$. Since server and clients only need to share $\vec p$, such a trade-off leads to a substantial improvement in communication cost. Moreover, we provide theoretical insight into our framework and establish a novel link between training-by-sampling and random convex geometry.

On the Sparsity of the Strong Lottery Ticket Hypothesis

Considerable research efforts have recently been made to show that a random neural network $N$ contains subnetworks capable of accurately approximating any given neural network that is sufficiently smaller than $N$, without any training. This line of research, known as the Strong Lottery Ticket Hypothesis (SLTH), was originally motivated by the weaker Lottery Ticket Hypothesis, which states that a sufficiently large random neural network $N$ contains \emph{sparse} subnetworks that can be trained efficiently to achieve performance comparable to that of training the entire network $N$. Despite its original motivation, results on the SLTH have so far not provided any guarantee on the size of subnetworks. Such limitation is due to the nature of the main technical tool leveraged by these results, the Random Subset Sum (RSS) Problem. Informally, the RSS Problem asks how large a random i.i.d. sample $\Omega$ should be so that we are able to approximate any number in $[-1,1]$, up to an error of $ \epsilon$, as the sum of a suitable subset of $\Omega$. We provide the first proof of the SLTH in classical settings, such as dense and equivariant networks, with guarantees on the sparsity of the subnetworks. Central to our results, is the proof of an essentially tight bound on the Random Fixed-Size Subset Sum Problem (RFSS), a variant of the RSS Problem in which we only ask for subsets of a given size, which is of independent interest.

Learning Hierarchically-Structured Concepts II: Overlapping Concepts, and Networks With Feedback

We continue our study from Lynch and Mallmann-Trenn (Neural Networks, 2021), of how concepts that have hierarchical structure might be represented in brain-like neural networks, how these representations might be used to recognize the concepts, and how these representations might be learned. In Lynch and Mallmann-Trenn (Neural Networks, 2021), we considered simple tree-structured concepts and feed-forward layered networks. Here we extend the model in two ways: we allow limited overlap between children of different concepts, and we allow networks to include feedback edges. For these more general cases, we describe and analyze algorithms for recognition and algorithms for learning.

Dynamic Crowd Vetting: Collaborative Detection of Malicious Robots in Dynamic Communication Networks

Coordination in a large number of networked robots is a challenging task, especially when robots are constantly moving around the environment and there are malicious attacks within the network. Various approaches in the literature exist for detecting malicious robots, such as message sampling or suspicious behavior analysis. However, these approaches require every robot to sample every other robot in the network, leading to a slow detection process that degrades team performance. This paper introduces a method that significantly decreases the detection time for legitimate robots to identify malicious robots in a scenario where legitimate robots are randomly moving around the environment. Our method leverages the concept of ``Dynamic Crowd Vetting" by utilizing observations from random encounters and trusted neighboring robots' opinions to quickly improve the accuracy of detecting malicious robots. The key intuition is that as long as each legitimate robot accurately estimates the legitimacy of at least some fixed subset of the team, the second-hand information they receive from trusted neighbors is enough to correct any misclassifications and provide accurate trust estimations of the rest of the team. We show that the size of this fixed subset can be characterized as a function of fundamental graph and random walk properties. Furthermore, we formally show that as the number of robots in the team increases the detection time remains constant. We develop a closed form expression for the critical number of time-steps required for our algorithm to successfully identify the true legitimacy of each robot to within a specified failure probability. Our theoretical results are validated through simulations demonstrating significant reductions in detection time when compared to previous works that do not leverage trusted neighbor information.

Beyond Impossibility: Balancing Sufficiency, Separation and Accuracy

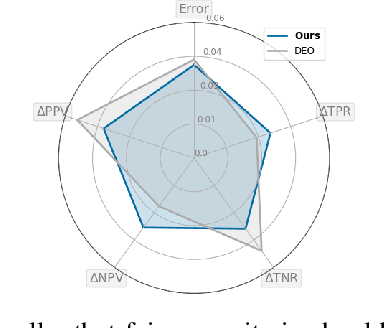
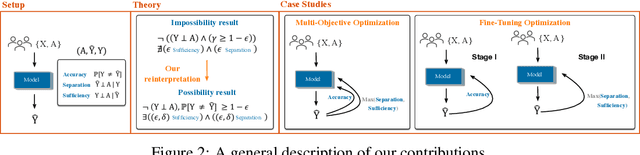
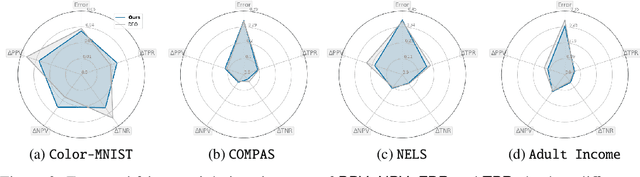
Among the various aspects of algorithmic fairness studied in recent years, the tension between satisfying both \textit{sufficiency} and \textit{separation} -- e.g. the ratios of positive or negative predictive values, and false positive or false negative rates across groups -- has received much attention. Following a debate sparked by COMPAS, a criminal justice predictive system, the academic community has responded by laying out important theoretical understanding, showing that one cannot achieve both with an imperfect predictor when there is no equal distribution of labels across the groups. In this paper, we shed more light on what might be still possible beyond the impossibility -- the existence of a trade-off means we should aim to find a good balance within it. After refining the existing theoretical result, we propose an objective that aims to balance \textit{sufficiency} and \textit{separation} measures, while maintaining similar accuracy levels. We show the use of such an objective in two empirical case studies, one involving a multi-objective framework, and the other fine-tuning of a model pre-trained for accuracy. We show promising results, where better trade-offs are achieved compared to existing alternatives.

Crowd Vetting: Rejecting Adversaries via Collaboration--with Application to Multi-Robot Flocking

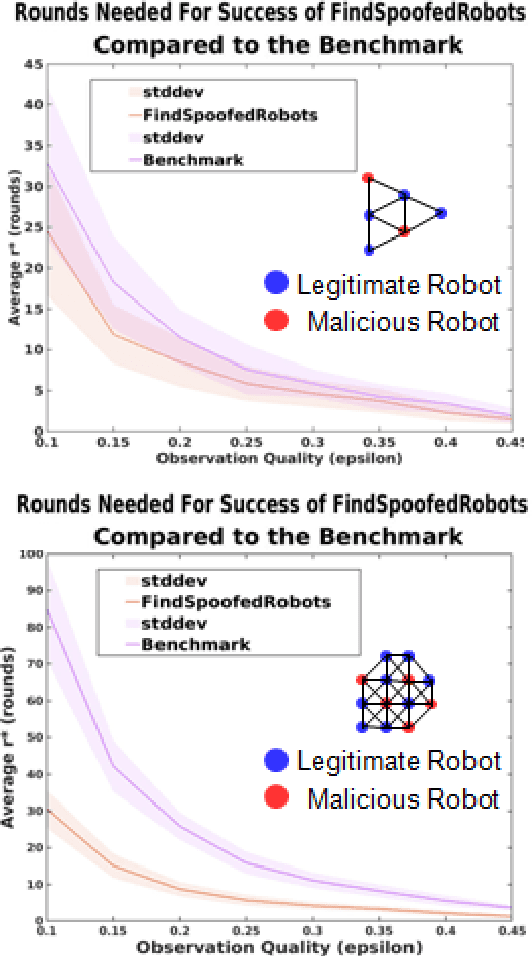
We characterize the advantage of using a robot's neighborhood to find and eliminate adversarial robots in the presence of a Sybil attack. We show that by leveraging the opinions of its neighbors on the trustworthiness of transmitted data, robots can detect adversaries with high probability. We characterize a number of communication rounds required to achieve this result to be a function of the communication quality and the proportion of legitimate to malicious robots. This result enables increased resiliency of many multi-robot algorithms. Because our results are finite time and not asymptotic, they are particularly well-suited for problems with a time critical nature. We develop two algorithms, \emph{FindSpoofedRobots} that determines trusted neighbors with high probability, and \emph{FindResilientAdjacencyMatrix} that enables distributed computation of graph properties in an adversarial setting. We apply our methods to a flocking problem where a team of robots must track a moving target in the presence of adversarial robots. We show that by using our algorithms, the team of robots are able to maintain tracking ability of the dynamic target.

Online Page Migration with ML Advice

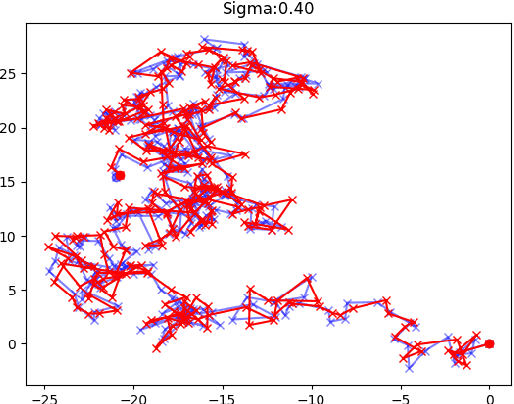
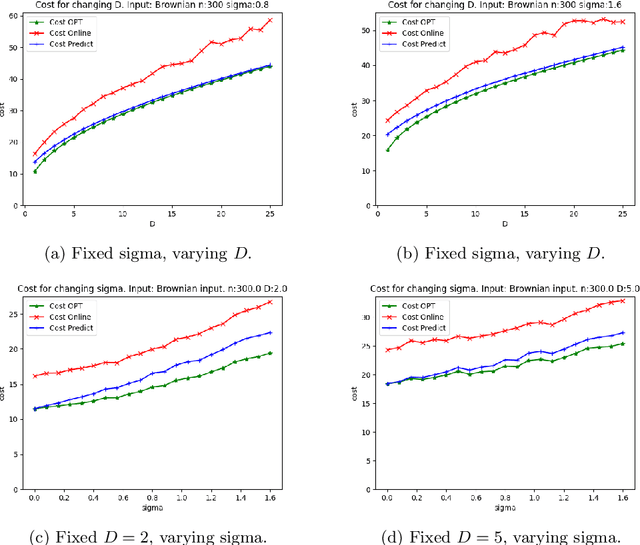
We consider online algorithms for the {\em page migration problem} that use predictions, potentially imperfect, to improve their performance. The best known online algorithms for this problem, due to Westbrook'94 and Bienkowski et al'17, have competitive ratios strictly bounded away from 1. In contrast, we show that if the algorithm is given a prediction of the input sequence, then it can achieve a competitive ratio that tends to $1$ as the prediction error rate tends to $0$. Specifically, the competitive ratio is equal to $1+O(q)$, where $q$ is the prediction error rate. We also design a ``fallback option'' that ensures that the competitive ratio of the algorithm for {\em any} input sequence is at most $O(1/q)$. Our result adds to the recent body of work that uses machine learning to improve the performance of ``classic'' algorithms.

Learning Hierarchically Structured Concepts

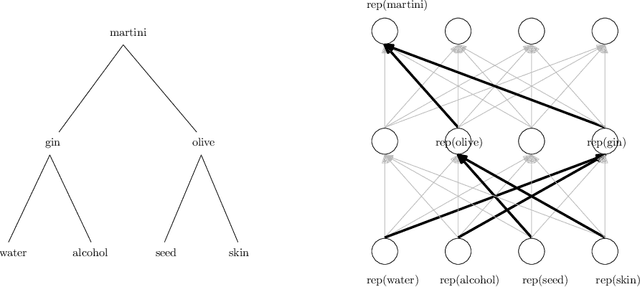
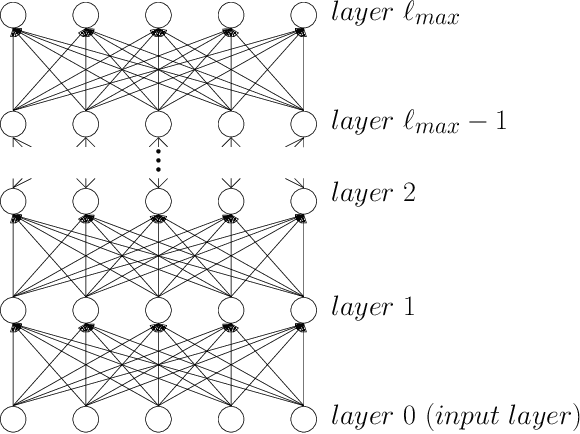
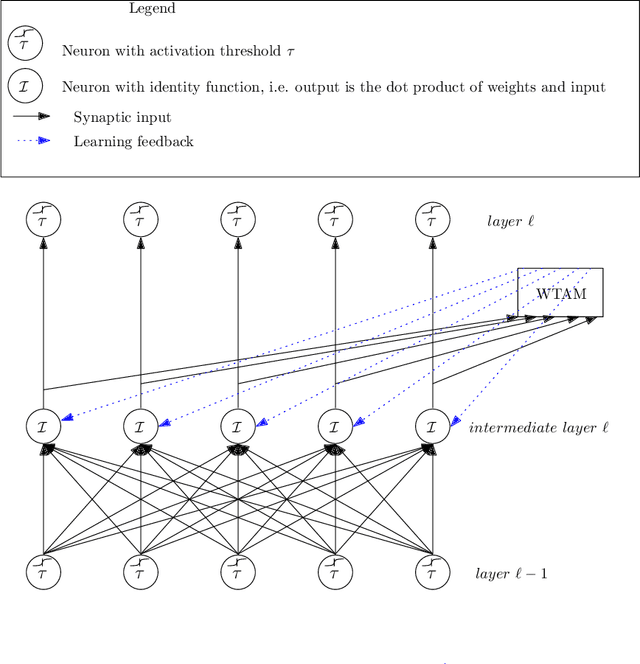
We study the question of how concepts that have structure get represented in the brain. Specifically, we introduce a model for hierarchically structured concepts and we show how a biologically plausible neural network can recognize these concepts, and how it can learn them in the first place. Our main goal is to introduce a general framework for these tasks and prove formally how both (recognition and learning) can be achieved. We show that both tasks can be accomplished even in presence of noise. For learning, we analyze Oja's rule formally, a well-known biologically-plausible rule for adjusting the weights of synapses. We complement the learning results with lower bounds asserting that, in order to recognize concepts of a certain hierarchical depth, neural networks must have a corresponding number of layers.

Instance-Optimality in the Noisy Value-and Comparison-Model --- Accept, Accept, Strong Accept: Which Papers get in?

Motivated by crowdsourced computation, peer-grading, and recommendation systems, Braverman, Mao and Weinberg [STOC'16] studied the \emph{query} and \emph{round} complexity of fundamental problems such as finding the maximum (\textsc{max}), finding all elements above a certain value (\textsc{threshold-$v$}) or computing the top$-k$ elements (\textsc{Top}-$k$) in a noisy environment. For example, consider the task of selecting papers for a conference. This task is challenging due the crowdsourcing nature of peer reviews: the results of reviews are noisy and it is necessary to parallelize the review process as much as possible. We study the noisy value model and the noisy comparison model: In the \emph{noisy value model}, a reviewer is asked to evaluate a single element: "What is the value of paper $i$?" (\eg accept). In the \emph{noisy comparison model} (introduced in the seminal work of Feige, Peleg, Raghavan and Upfal [SICOMP'94]) a reviewer is asked to do a pairwise comparison: "Is paper $i$ better than paper $j$?" In this paper, we show optimal worst-case query complexity for the \textsc{max},\textsc{threshold-$v$} and \textsc{Top}-$k$ problems. For \textsc{max} and \textsc{Top}-$k$, we obtain optimal worst-case upper and lower bounds on the round vs query complexity in both models. For \textsc{threshold}-$v$, we obtain optimal query complexity and nearly-optimal round complexity, where $k$ is the size of the output) for both models. We then go beyond the worst-case and address the question of the importance of knowledge of the instance by providing, for a large range of parameters, instance-optimal algorithms with respect to the query complexity. Furthermore, we show that the value model is strictly easier than the comparison model.

Hierarchical Clustering: Objective Functions and Algorithms

Hierarchical clustering is a recursive partitioning of a dataset into clusters at an increasingly finer granularity. Motivated by the fact that most work on hierarchical clustering was based on providing algorithms, rather than optimizing a specific objective, Dasgupta framed similarity-based hierarchical clustering as a combinatorial optimization problem, where a `good' hierarchical clustering is one that minimizes some cost function. He showed that this cost function has certain desirable properties. We take an axiomatic approach to defining `good' objective functions for both similarity and dissimilarity-based hierarchical clustering. We characterize a set of "admissible" objective functions (that includes Dasgupta's one) that have the property that when the input admits a `natural' hierarchical clustering, it has an optimal value. Equipped with a suitable objective function, we analyze the performance of practical algorithms, as well as develop better algorithms. For similarity-based hierarchical clustering, Dasgupta showed that the divisive sparsest-cut approach achieves an $O(\log^{3/2} n)$-approximation. We give a refined analysis of the algorithm and show that it in fact achieves an $O(\sqrt{\log n})$-approx. (Charikar and Chatziafratis independently proved that it is a $O(\sqrt{\log n})$-approx.). This improves upon the LP-based $O(\log n)$-approx. of Roy and Pokutta. For dissimilarity-based hierarchical clustering, we show that the classic average-linkage algorithm gives a factor 2 approx., and provide a simple and better algorithm that gives a factor 3/2 approx.. Finally, we consider `beyond-worst-case' scenario through a generalisation of the stochastic block model for hierarchical clustering. We show that Dasgupta's cost function has desirable properties for these inputs and we provide a simple 1 + o(1)-approximation in this setting.