Online Page Migration with ML Advice
Paper and Code
Jun 09, 2020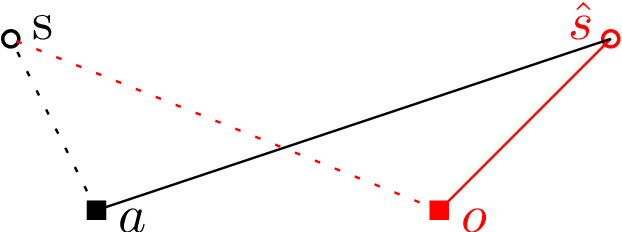
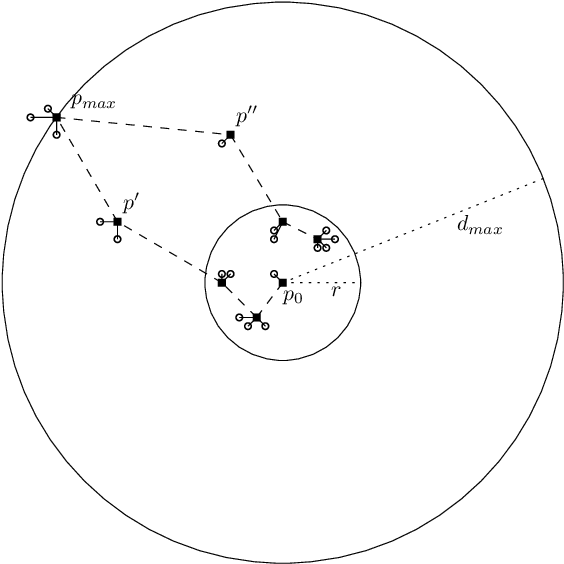
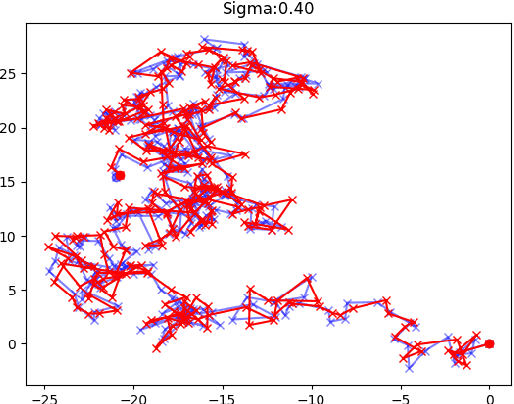
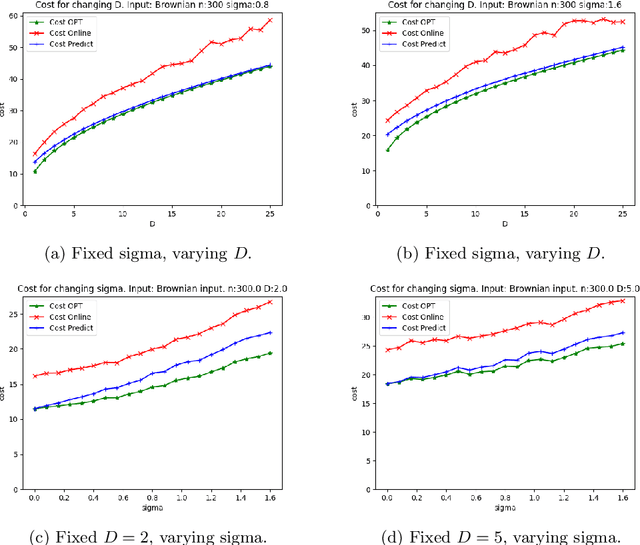
We consider online algorithms for the {\em page migration problem} that use predictions, potentially imperfect, to improve their performance. The best known online algorithms for this problem, due to Westbrook'94 and Bienkowski et al'17, have competitive ratios strictly bounded away from 1. In contrast, we show that if the algorithm is given a prediction of the input sequence, then it can achieve a competitive ratio that tends to $1$ as the prediction error rate tends to $0$. Specifically, the competitive ratio is equal to $1+O(q)$, where $q$ is the prediction error rate. We also design a ``fallback option'' that ensures that the competitive ratio of the algorithm for {\em any} input sequence is at most $O(1/q)$. Our result adds to the recent body of work that uses machine learning to improve the performance of ``classic'' algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge