Crowd Vetting: Rejecting Adversaries via Collaboration--with Application to Multi-Robot Flocking
Paper and Code
Dec 11, 2020


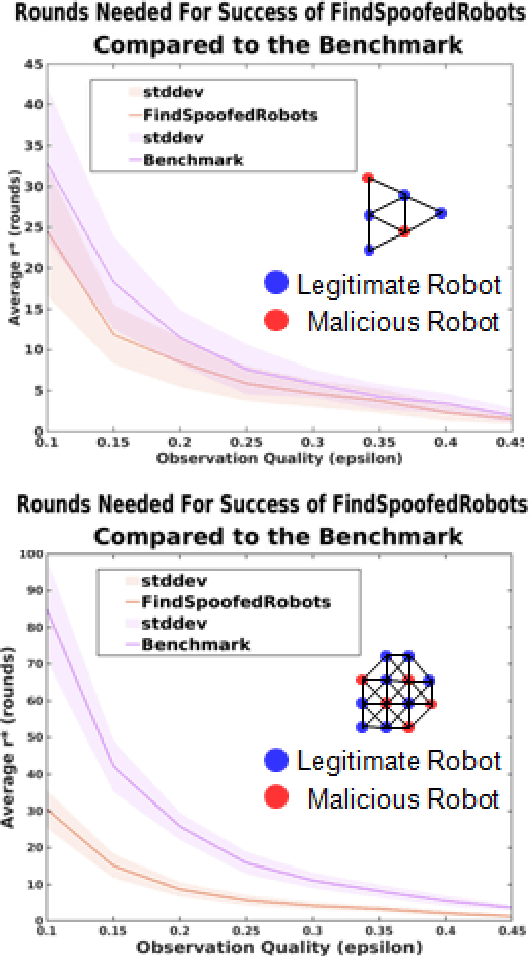
We characterize the advantage of using a robot's neighborhood to find and eliminate adversarial robots in the presence of a Sybil attack. We show that by leveraging the opinions of its neighbors on the trustworthiness of transmitted data, robots can detect adversaries with high probability. We characterize a number of communication rounds required to achieve this result to be a function of the communication quality and the proportion of legitimate to malicious robots. This result enables increased resiliency of many multi-robot algorithms. Because our results are finite time and not asymptotic, they are particularly well-suited for problems with a time critical nature. We develop two algorithms, \emph{FindSpoofedRobots} that determines trusted neighbors with high probability, and \emph{FindResilientAdjacencyMatrix} that enables distributed computation of graph properties in an adversarial setting. We apply our methods to a flocking problem where a team of robots must track a moving target in the presence of adversarial robots. We show that by using our algorithms, the team of robots are able to maintain tracking ability of the dynamic target.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge