Trading-off Accuracy and Communication Cost in Federated Learning

Leveraging the training-by-pruning paradigm introduced by Zhou et al. and Isik et al. introduced a federated learning protocol that achieves a 34-fold reduction in communication cost. We achieve a compression improvements of orders of orders of magnitude over the state-of-the-art. The central idea of our framework is to encode the network weights $\vec w$ by a the vector of trainable parameters $\vec p$, such that $\vec w = Q\cdot \vec p$ where $Q$ is a carefully-generate sparse random matrix (that remains fixed throughout training). In such framework, the previous work of Zhou et al. [NeurIPS'19] is retrieved when $Q$ is diagonal and $\vec p$ has the same dimension of $\vec w$. We instead show that $\vec p$ can effectively be chosen much smaller than $\vec w$, while retaining the same accuracy at the price of a decrease of the sparsity of $Q$. Since server and clients only need to share $\vec p$, such a trade-off leads to a substantial improvement in communication cost. Moreover, we provide theoretical insight into our framework and establish a novel link between training-by-sampling and random convex geometry.

Relating Piecewise Linear Kolmogorov Arnold Networks to ReLU Networks

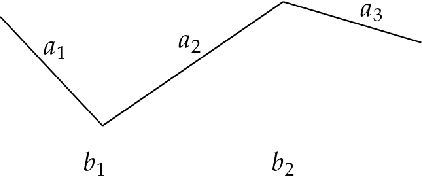
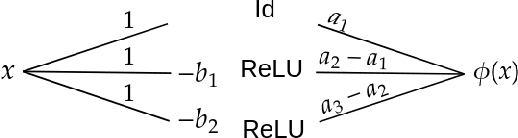
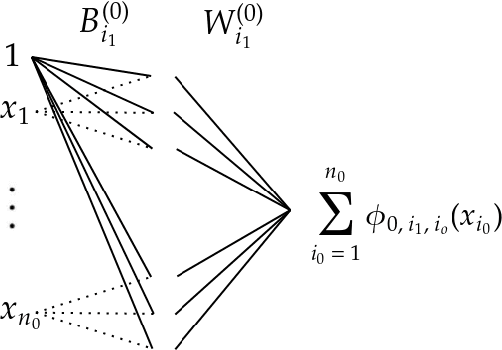
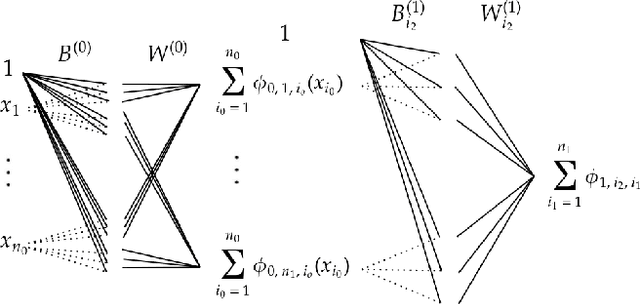
Kolmogorov-Arnold Networks are a new family of neural network architectures which holds promise for overcoming the curse of dimensionality and has interpretability benefits (arXiv:2404.19756). In this paper, we explore the connection between Kolmogorov Arnold Networks (KANs) with piecewise linear (univariate real) functions and ReLU networks. We provide completely explicit constructions to convert a piecewise linear KAN into a ReLU network and vice versa.

The Topos of Transformer Networks

The transformer neural network has significantly out-shined all other neural network architectures as the engine behind large language models. We provide a theoretical analysis of the expressivity of the transformer architecture through the lens of topos theory. From this viewpoint, we show that many common neural network architectures, such as the convolutional, recurrent and graph convolutional networks, can be embedded in a pretopos of piecewise-linear functions, but that the transformer necessarily lives in its topos completion. In particular, this suggests that the two network families instantiate different fragments of logic: the former are first order, whereas transformers are higher-order reasoners. Furthermore, we draw parallels with architecture search and gradient descent, integrating our analysis in the framework of cybernetic agents.

Any Deep ReLU Network is Shallow

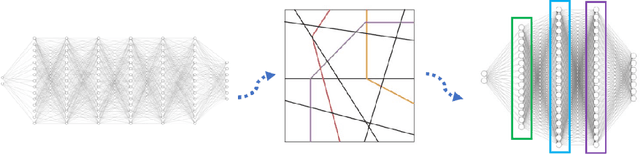
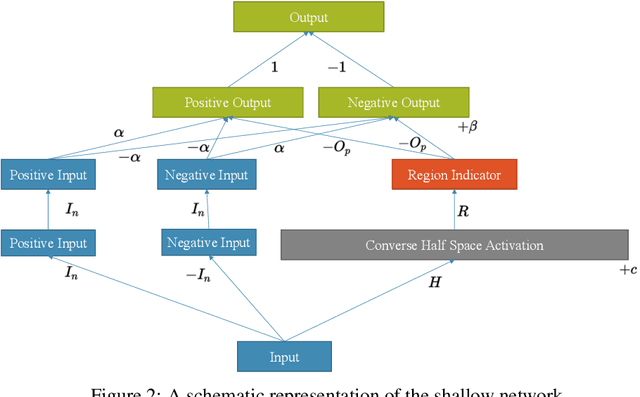
We constructively prove that every deep ReLU network can be rewritten as a functionally identical three-layer network with weights valued in the extended reals. Based on this proof, we provide an algorithm that, given a deep ReLU network, finds the explicit weights of the corresponding shallow network. The resulting shallow network is transparent and used to generate explanations of the model s behaviour.

Unwrapping All ReLU Networks

Deep ReLU Networks can be decomposed into a collection of linear models, each defined in a region of a partition of the input space. This paper provides three results extending this theory. First, we extend this linear decompositions to Graph Neural networks and tensor convolutional networks, as well as networks with multiplicative interactions. Second, we provide proofs that neural networks can be understood as interpretable models such as Multivariate Decision trees and logical theories. Finally, we show how this model leads to computing cheap and exact SHAP values. We validate the theory through experiments with on Graph Neural Networks.