Small is Sufficient: Reducing the World AI Energy Consumption Through Model Selection

The energy consumption and carbon footprint of Artificial Intelligence (AI) have become critical concerns due to rising costs and environmental impacts. In response, a new trend in green AI is emerging, shifting from the "bigger is better" paradigm, which prioritizes large models, to "small is sufficient", emphasizing energy sobriety through smaller, more efficient models. We explore how the AI community can adopt energy sobriety today by focusing on model selection during inference. Model selection consists of choosing the most appropriate model for a given task, a simple and readily applicable method, unlike approaches requiring new hardware or architectures. Our hypothesis is that, as in many industrial activities, marginal utility gains decrease with increasing model size. Thus, applying model selection can significantly reduce energy consumption while maintaining good utility for AI inference. We conduct a systematic study of AI tasks, analyzing their popularity, model size, and efficiency. We examine how the maturity of different tasks and model adoption patterns impact the achievable energy savings, ranging from 1% to 98% for different tasks. Our estimates indicate that applying model selection could reduce AI energy consumption by 27.8%, saving 31.9 TWh worldwide in 2025 - equivalent to the annual output of five nuclear power reactors.

Attribute Inference Attacks for Federated Regression Tasks

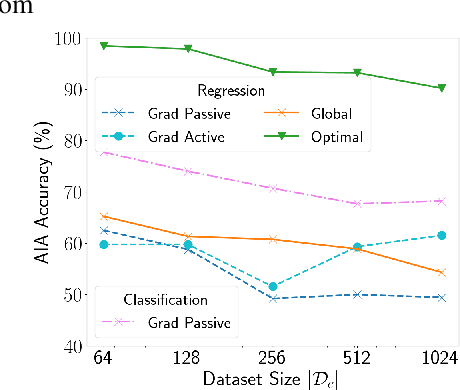
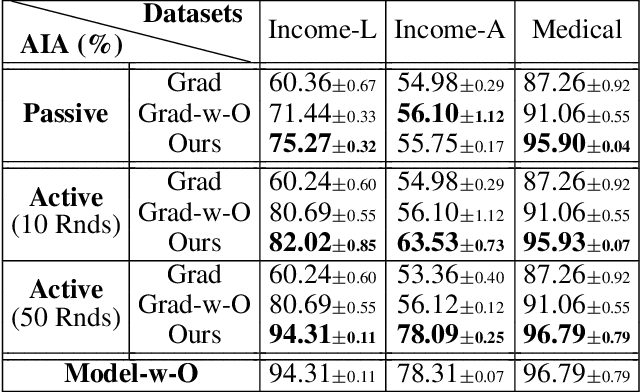
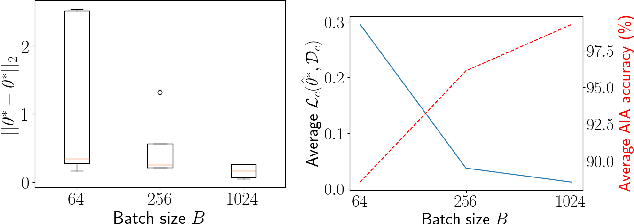
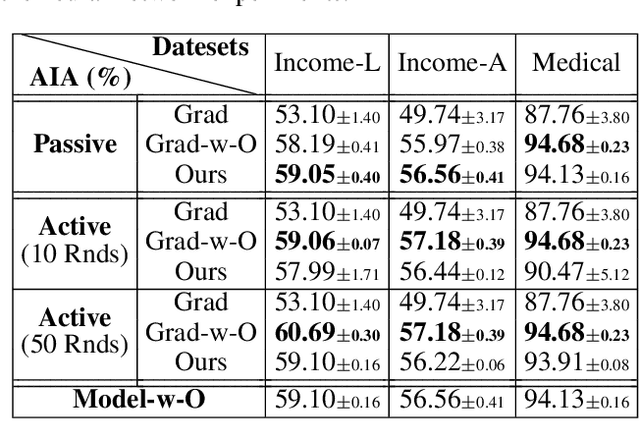
Federated Learning (FL) enables multiple clients, such as mobile phones and IoT devices, to collaboratively train a global machine learning model while keeping their data localized. However, recent studies have revealed that the training phase of FL is vulnerable to reconstruction attacks, such as attribute inference attacks (AIA), where adversaries exploit exchanged messages and auxiliary public information to uncover sensitive attributes of targeted clients. While these attacks have been extensively studied in the context of classification tasks, their impact on regression tasks remains largely unexplored. In this paper, we address this gap by proposing novel model-based AIAs specifically designed for regression tasks in FL environments. Our approach considers scenarios where adversaries can either eavesdrop on exchanged messages or directly interfere with the training process. We benchmark our proposed attacks against state-of-the-art methods using real-world datasets. The results demonstrate a significant increase in reconstruction accuracy, particularly in heterogeneous client datasets, a common scenario in FL. The efficacy of our model-based AIAs makes them better candidates for empirically quantifying privacy leakage for federated regression tasks.

On the Sparsity of the Strong Lottery Ticket Hypothesis

Considerable research efforts have recently been made to show that a random neural network $N$ contains subnetworks capable of accurately approximating any given neural network that is sufficiently smaller than $N$, without any training. This line of research, known as the Strong Lottery Ticket Hypothesis (SLTH), was originally motivated by the weaker Lottery Ticket Hypothesis, which states that a sufficiently large random neural network $N$ contains \emph{sparse} subnetworks that can be trained efficiently to achieve performance comparable to that of training the entire network $N$. Despite its original motivation, results on the SLTH have so far not provided any guarantee on the size of subnetworks. Such limitation is due to the nature of the main technical tool leveraged by these results, the Random Subset Sum (RSS) Problem. Informally, the RSS Problem asks how large a random i.i.d. sample $\Omega$ should be so that we are able to approximate any number in $[-1,1]$, up to an error of $ \epsilon$, as the sum of a suitable subset of $\Omega$. We provide the first proof of the SLTH in classical settings, such as dense and equivariant networks, with guarantees on the sparsity of the subnetworks. Central to our results, is the proof of an essentially tight bound on the Random Fixed-Size Subset Sum Problem (RFSS), a variant of the RSS Problem in which we only ask for subsets of a given size, which is of independent interest.