Conditioning Diffusions Using Malliavin Calculus

In stochastic optimal control and conditional generative modelling, a central computational task is to modify a reference diffusion process to maximise a given terminal-time reward. Most existing methods require this reward to be differentiable, using gradients to steer the diffusion towards favourable outcomes. However, in many practical settings, like diffusion bridges, the reward is singular, taking an infinite value if the target is hit and zero otherwise. We introduce a novel framework, based on Malliavin calculus and path-space integration by parts, that enables the development of methods robust to such singular rewards. This allows our approach to handle a broad range of applications, including classification, diffusion bridges, and conditioning without the need for artificial observational noise. We demonstrate that our approach offers stable and reliable training, outperforming existing techniques.

Stein transport for Bayesian inference

We introduce $\textit{Stein transport}$, a novel methodology for Bayesian inference designed to efficiently push an ensemble of particles along a predefined curve of tempered probability distributions. The driving vector field is chosen from a reproducing kernel Hilbert space and can be derived either through a suitable kernel ridge regression formulation or as an infinitesimal optimal transport map in the Stein geometry. The update equations of Stein transport resemble those of Stein variational gradient descent (SVGD), but introduce a time-varying score function as well as specific weights attached to the particles. While SVGD relies on convergence in the long-time limit, Stein transport reaches its posterior approximation at finite time $t=1$. Studying the mean-field limit, we discuss the errors incurred by regularisation and finite-particle effects, and we connect Stein transport to birth-death dynamics and Fisher-Rao gradient flows. In a series of experiments, we show that in comparison to SVGD, Stein transport not only often reaches more accurate posterior approximations with a significantly reduced computational budget, but that it also effectively mitigates the variance collapse phenomenon commonly observed in SVGD.

From continuous-time formulations to discretization schemes: tensor trains and robust regression for BSDEs and parabolic PDEs

The numerical approximation of partial differential equations (PDEs) poses formidable challenges in high dimensions since classical grid-based methods suffer from the so-called curse of dimensionality. Recent attempts rely on a combination of Monte Carlo methods and variational formulations, using neural networks for function approximation. Extending previous work (Richter et al., 2021), we argue that tensor trains provide an appealing framework for parabolic PDEs: The combination of reformulations in terms of backward stochastic differential equations and regression-type methods holds the promise of leveraging latent low-rank structures, enabling both compression and efficient computation. Emphasizing a continuous-time viewpoint, we develop iterative schemes, which differ in terms of computational efficiency and robustness. We demonstrate both theoretically and numerically that our methods can achieve a favorable trade-off between accuracy and computational efficiency. While previous methods have been either accurate or fast, we have identified a novel numerical strategy that can often combine both of these aspects.

Transport, Variational Inference and Diffusions: with Applications to Annealed Flows and Schrödinger Bridges

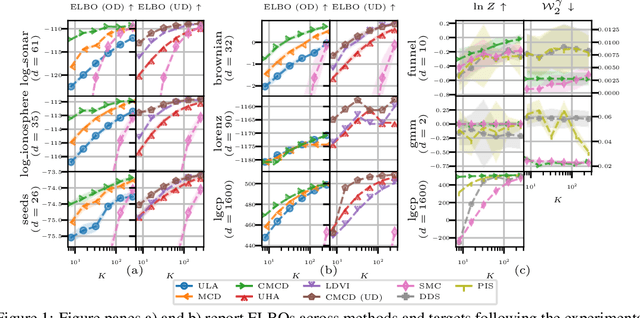
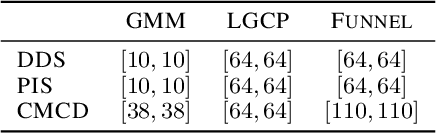
This paper explores the connections between optimal transport and variational inference, with a focus on forward and reverse time stochastic differential equations and Girsanov transformations.We present a principled and systematic framework for sampling and generative modelling centred around divergences on path space. Our work culminates in the development of a novel score-based annealed flow technique (with connections to Jarzynski and Crooks identities from statistical physics) and a regularised iterative proportional fitting (IPF)-type objective, departing from the sequential nature of standard IPF. Through a series of generative modelling examples and a double-well-based rare event task, we showcase the potential of the proposed methods.

Bayesian Learning via Neural Schrödinger-Föllmer Flows

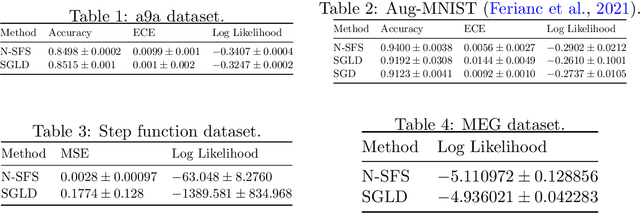
In this work we explore a new framework for approximate Bayesian inference in large datasets based on stochastic control. We advocate stochastic control as a finite time and low variance alternative to popular steady-state methods such as stochastic gradient Langevin dynamics (SGLD). Furthermore, we discuss and adapt the existing theoretical guarantees of this framework and establish connections to already existing VI routines in SDE-based models.

Interpolating between BSDEs and PINNs -- deep learning for elliptic and parabolic boundary value problems

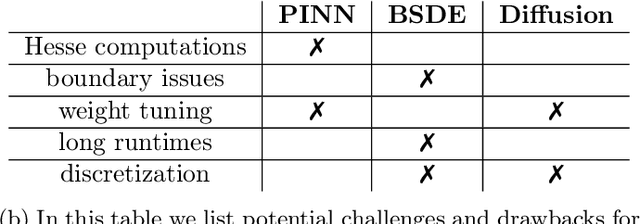
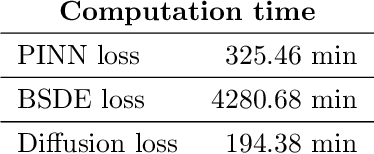
Solving high-dimensional partial differential equations is a recurrent challenge in economics, science and engineering. In recent years, a great number of computational approaches have been developed, most of them relying on a combination of Monte Carlo sampling and deep learning based approximation. For elliptic and parabolic problems, existing methods can broadly be classified into those resting on reformulations in terms of $\textit{backward stochastic differential equations}$ (BSDEs) and those aiming to minimize a regression-type $L^2$-error ($\textit{physics-informed neural networks}$, PINNs). In this paper, we review the literature and suggest a methodology based on the novel $\textit{diffusion loss}$ that interpolates between BSDEs and PINNs. Our contribution opens the door towards a unified understanding of numerical approaches for high-dimensional PDEs, as well as for implementations that combine the strengths of BSDEs and PINNs. We also provide generalizations to eigenvalue problems and perform extensive numerical studies, including calculations of the ground state for nonlinear Schr\"odinger operators and committor functions relevant in molecular dynamics.

Stein Variational Gradient Descent: many-particle and long-time asymptotics

Stein variational gradient descent (SVGD) refers to a class of methods for Bayesian inference based on interacting particle systems. In this paper, we consider the originally proposed deterministic dynamics as well as a stochastic variant, each of which represent one of the two main paradigms in Bayesian computational statistics: variational inference and Markov chain Monte Carlo. As it turns out, these are tightly linked through a correspondence between gradient flow structures and large-deviation principles rooted in statistical physics. To expose this relationship, we develop the cotangent space construction for the Stein geometry, prove its basic properties, and determine the large-deviation functional governing the many-particle limit for the empirical measure. Moreover, we identify the Stein-Fisher information (or kernelised Stein discrepancy) as its leading order contribution in the long-time and many-particle regime in the sense of $\Gamma$-convergence, shedding some light on the finite-particle properties of SVGD. Finally, we establish a comparison principle between the Stein-Fisher information and RKHS-norms that might be of independent interest.

Solving high-dimensional parabolic PDEs using the tensor train format

High-dimensional partial differential equations (PDEs) are ubiquitous in economics, science and engineering. However, their numerical treatment poses formidable challenges since traditional grid-based methods tend to be frustrated by the curse of dimensionality. In this paper, we argue that tensor trains provide an appealing approximation framework for parabolic PDEs: the combination of reformulations in terms of backward stochastic differential equations and regression-type methods in the tensor format holds the promise of leveraging latent low-rank structures enabling both compression and efficient computation. Following this paradigm, we develop novel iterative schemes, involving either explicit and fast or implicit and accurate updates. We demonstrate in a number of examples that our methods achieve a favorable trade-off between accuracy and computational efficiency in comparison with state-of-the-art neural network based approaches.

VarGrad: A Low-Variance Gradient Estimator for Variational Inference

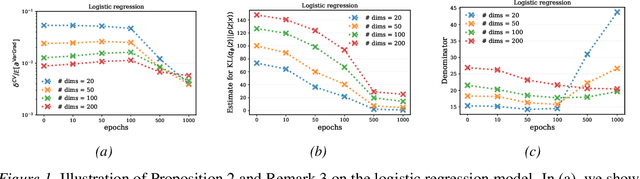
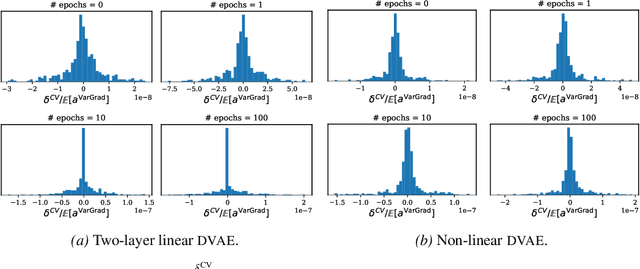
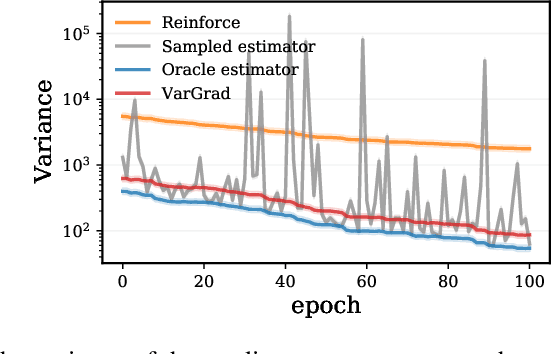
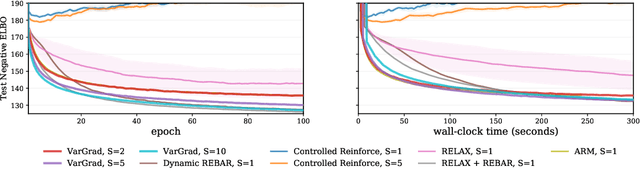
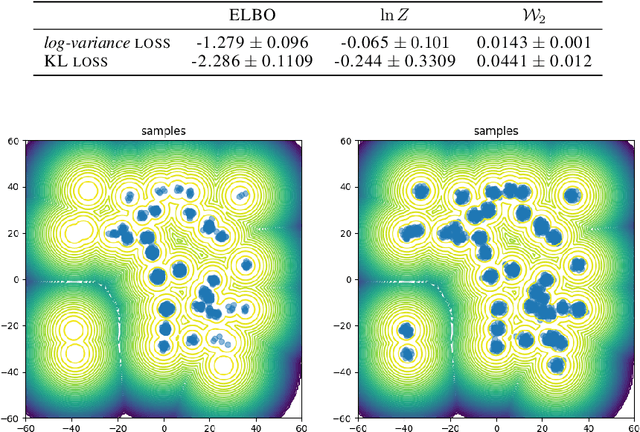
We analyse the properties of an unbiased gradient estimator of the ELBO for variational inference, based on the score function method with leave-one-out control variates. We show that this gradient estimator can be obtained using a new loss, defined as the variance of the log-ratio between the exact posterior and the variational approximation, which we call the $\textit{log-variance loss}$. Under certain conditions, the gradient of the log-variance loss equals the gradient of the (negative) ELBO. We show theoretically that this gradient estimator, which we call $\textit{VarGrad}$ due to its connection to the log-variance loss, exhibits lower variance than the score function method in certain settings, and that the leave-one-out control variate coefficients are close to the optimal ones. We empirically demonstrate that VarGrad offers a favourable variance versus computation trade-off compared to other state-of-the-art estimators on a discrete VAE.

Solving high-dimensional Hamilton-Jacobi-Bellman PDEs using neural networks: perspectives from the theory of controlled diffusions and measures on path space

Optimal control of diffusion processes is intimately connected to the problem of solving certain Hamilton-Jacobi-Bellman equations. Building on recent machine learning inspired approaches towards high-dimensional PDEs, we investigate the potential of iterative diffusion optimisation techniques, in particular considering applications in importance sampling and rare event simulation. The choice of an appropriate loss function being a central element in the algorithmic design, we develop a principled framework based on divergences between path measures, encompassing various existing methods. Motivated by connections to forward-backward SDEs, we propose and study the novel log-variance divergence, showing favourable properties of corresponding Monte Carlo estimators. The promise of the developed approach is exemplified by a range of high-dimensional and metastable numerical examples.