When Does Re-initialization Work?

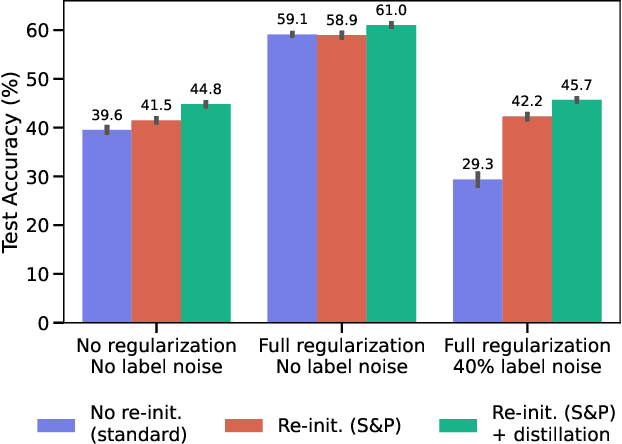
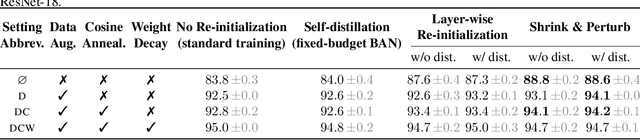
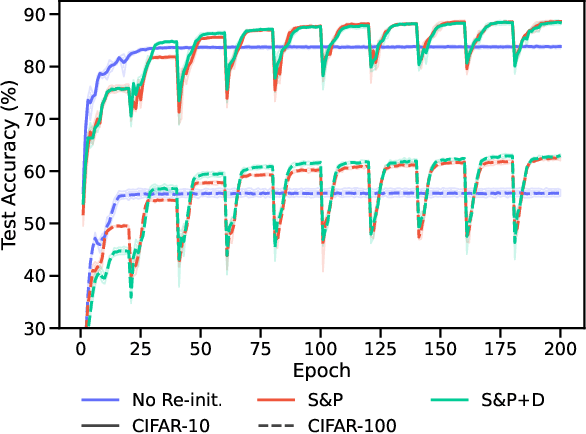
Re-initializing a neural network during training has been observed to improve generalization in recent works. Yet it is neither widely adopted in deep learning practice nor is it often used in state-of-the-art training protocols. This raises the question of when re-initialization works, and whether it should be used together with regularization techniques such as data augmentation, weight decay and learning rate schedules. In this work, we conduct an extensive empirical comparison of standard training with a selection of re-initialization methods to answer this question, training over 15,000 models on a variety of image classification benchmarks. We first establish that such methods are consistently beneficial for generalization in the absence of any other regularization. However, when deployed alongside other carefully tuned regularization techniques, re-initialization methods offer little to no added benefit for generalization, although optimal generalization performance becomes less sensitive to the choice of learning rate and weight decay hyperparameters. To investigate the impact of re-initialization methods on noisy data, we also consider learning under label noise. Surprisingly, in this case, re-initialization significantly improves upon standard training, even in the presence of other carefully tuned regularization techniques.

Pre-training via Denoising for Molecular Property Prediction

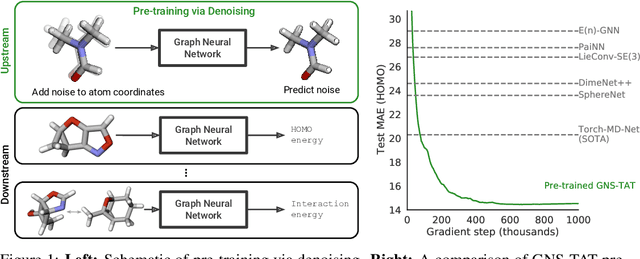
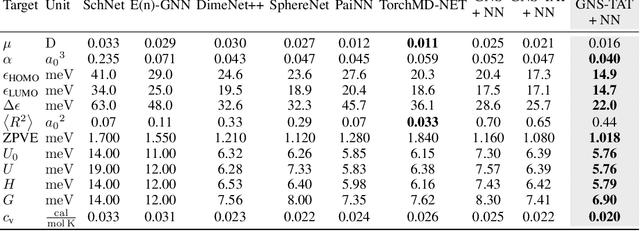
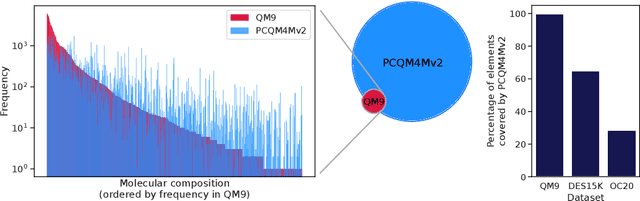
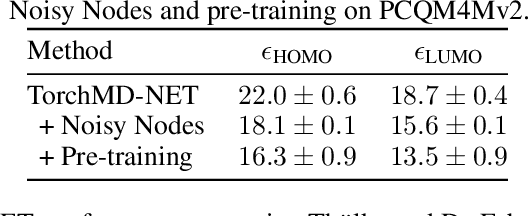
Many important problems involving molecular property prediction from 3D structures have limited data, posing a generalization challenge for neural networks. In this paper, we describe a pre-training technique that utilizes large datasets of 3D molecular structures at equilibrium to learn meaningful representations for downstream tasks. Inspired by recent advances in noise regularization, our pre-training objective is based on denoising. Relying on the well-known link between denoising autoencoders and score-matching, we also show that the objective corresponds to learning a molecular force field -- arising from approximating the physical state distribution with a mixture of Gaussians -- directly from equilibrium structures. Our experiments demonstrate that using this pre-training objective significantly improves performance on multiple benchmarks, achieving a new state-of-the-art on the majority of targets in the widely used QM9 dataset. Our analysis then provides practical insights into the effects of different factors -- dataset sizes, model size and architecture, and the choice of upstream and downstream datasets -- on pre-training.

Provably Strict Generalisation Benefit for Equivariant Models

It is widely believed that engineering a model to be invariant/equivariant improves generalisation. Despite the growing popularity of this approach, a precise characterisation of the generalisation benefit is lacking. By considering the simplest case of linear models, this paper provides the first provably non-zero improvement in generalisation for invariant/equivariant models when the target distribution is invariant/equivariant with respect to a compact group. Moreover, our work reveals an interesting relationship between generalisation, the number of training examples and properties of the group action. Our results rest on an observation of the structure of function spaces under averaging operators which, along with its consequences for feature averaging, may be of independent interest.

LieTransformer: Equivariant self-attention for Lie Groups

Group equivariant neural networks are used as building blocks of group invariant neural networks, which have been shown to improve generalisation performance and data efficiency through principled parameter sharing. Such works have mostly focused on group equivariant convolutions, building on the result that group equivariant linear maps are necessarily convolutions. In this work, we extend the scope of the literature to non-linear neural network modules, namely self-attention, that is emerging as a prominent building block of deep learning models. We propose the LieTransformer, an architecture composed of LieSelfAttention layers that are equivariant to arbitrary Lie groups and their discrete subgroups. We demonstrate the generality of our approach by showing experimental results that are competitive to baseline methods on a wide range of tasks: shape counting on point clouds, molecular property regression and modelling particle trajectories under Hamiltonian dynamics.

Neural Ensemble Search for Performant and Calibrated Predictions

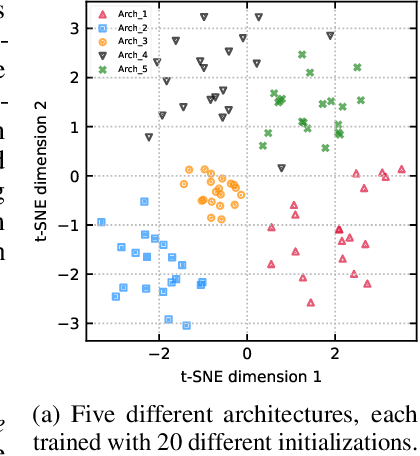
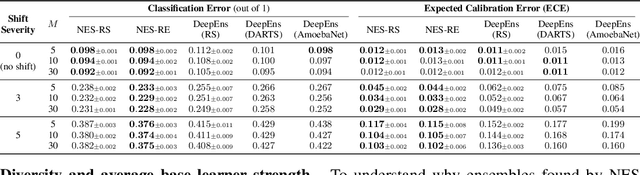
Ensembles of neural networks achieve superior performance compared to stand-alone networks not only in terms of accuracy on in-distribution data but also on data with distributional shift alongside improved uncertainty calibration. Diversity among networks in an ensemble is believed to be key for building strong ensembles, but typical approaches only ensemble different weight vectors of a fixed architecture. Instead, we investigate neural architecture search (NAS) for explicitly constructing ensembles to exploit diversity among networks of varying architectures and to achieve robustness against distributional shift. By directly optimizing ensemble performance, our methods implicitly encourage diversity among networks, without the need to explicitly define diversity. We find that the resulting ensembles are more diverse compared to ensembles composed of a fixed architecture and are therefore also more powerful. We show significant improvements in ensemble performance on image classification tasks both for in-distribution data and during distributional shift with better uncertainty calibration.