A practical guide to machine learning interatomic potentials -- Status and future

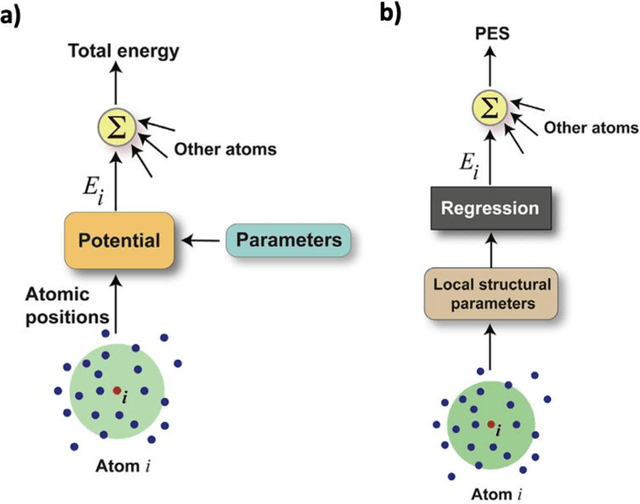
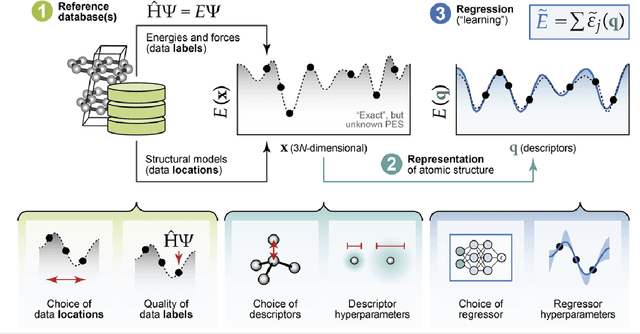
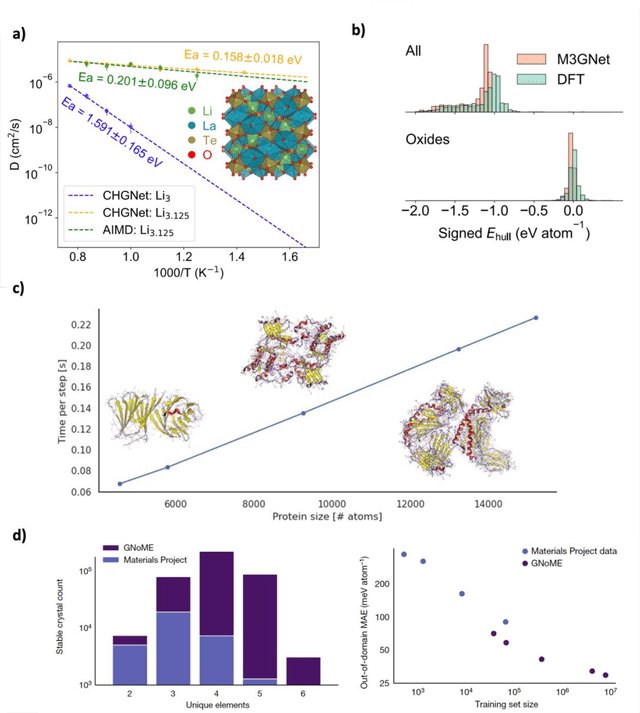
The rapid development and large body of literature on machine learning interatomic potentials (MLIPs) can make it difficult to know how to proceed for researchers who are not experts but wish to use these tools. The spirit of this review is to help such researchers by serving as a practical, accessible guide to the state-of-the-art in MLIPs. This review paper covers a broad range of topics related to MLIPs, including (i) central aspects of how and why MLIPs are enablers of many exciting advancements in molecular modeling, (ii) the main underpinnings of different types of MLIPs, including their basic structure and formalism, (iii) the potentially transformative impact of universal MLIPs for both organic and inorganic systems, including an overview of the most recent advances, capabilities, downsides, and potential applications of this nascent class of MLIPs, (iv) a practical guide for estimating and understanding the execution speed of MLIPs, including guidance for users based on hardware availability, type of MLIP used, and prospective simulation size and time, (v) a manual for what MLIP a user should choose for a given application by considering hardware resources, speed requirements, energy and force accuracy requirements, as well as guidance for choosing pre-trained potentials or fitting a new potential from scratch, (vi) discussion around MLIP infrastructure, including sources of training data, pre-trained potentials, and hardware resources for training, (vii) summary of some key limitations of present MLIPs and current approaches to mitigate such limitations, including methods of including long-range interactions, handling magnetic systems, and treatment of excited states, and finally (viii) we finish with some more speculative thoughts on what the future holds for the development and application of MLIPs over the next 3-10+ years.

Analysis of static and dynamic batching algorithms for graph neural networks

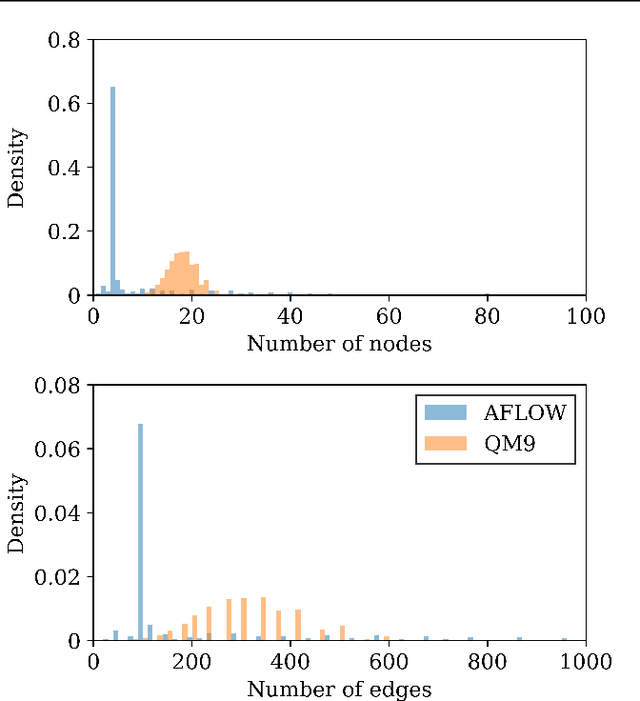
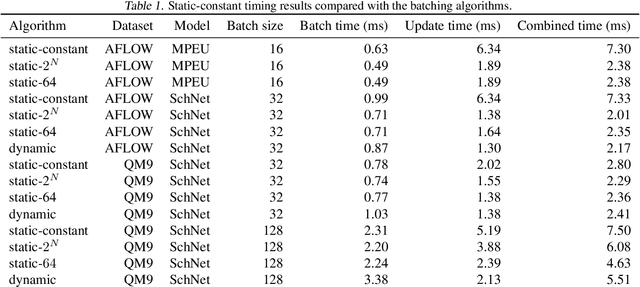
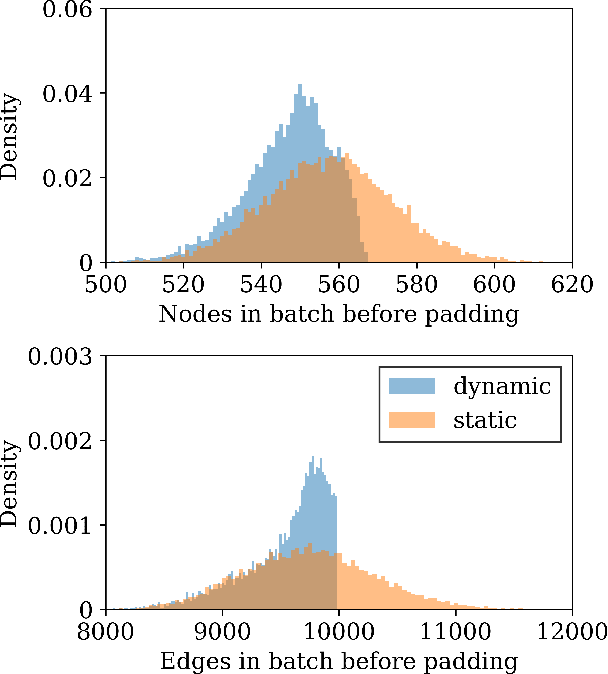
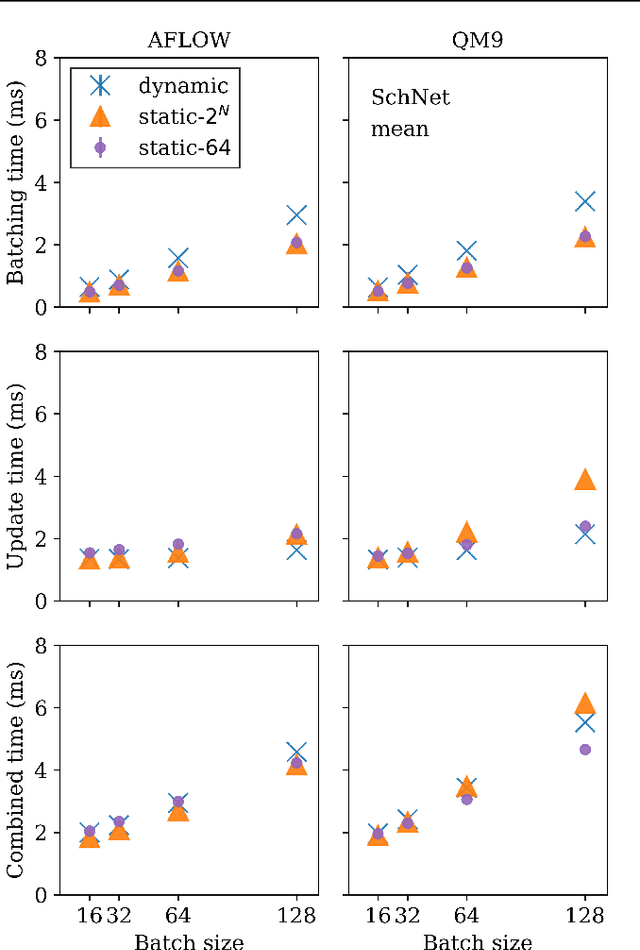
Graph neural networks (GNN) have shown promising results for several domains such as materials science, chemistry, and the social sciences. GNN models often contain millions of parameters, and like other neural network (NN) models, are often fed only a fraction of the graphs that make up the training dataset in batches to update model parameters. The effect of batching algorithms on training time and model performance has been thoroughly explored for NNs but not yet for GNNs. We analyze two different batching algorithms for graph based models, namely static and dynamic batching. We use the Jraph library built on JAX to perform our experiments, where we compare the two batching methods for two datasets, the QM9 dataset of small molecules and the AFLOW materials database. Our experiments show that significant training time savings can be found from changing the batching algorithm, but the fastest algorithm depends on the data, model, batch size and number of training steps run. Experiments show no significant difference in model learning between the algorithms.

Orb: A Fast, Scalable Neural Network Potential

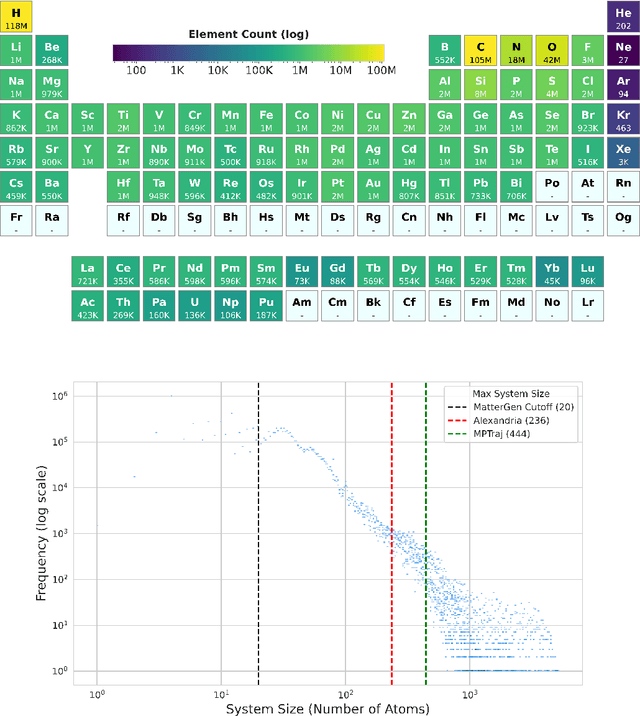
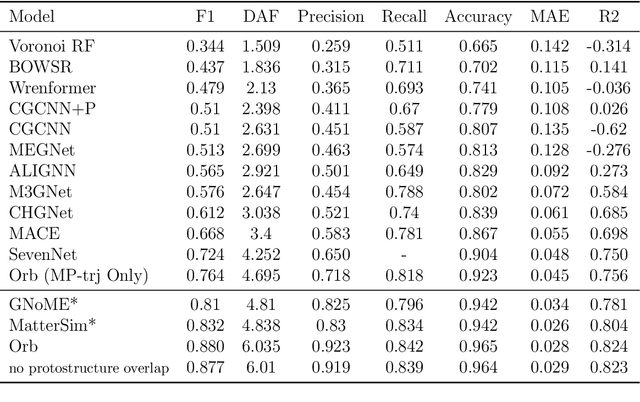
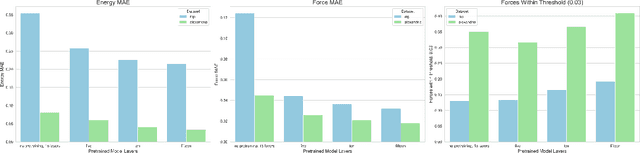
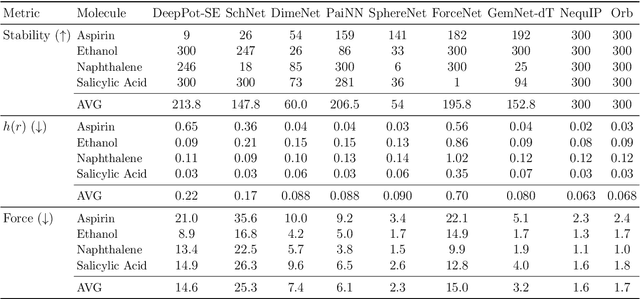
We introduce Orb, a family of universal interatomic potentials for atomistic modelling of materials. Orb models are 3-6 times faster than existing universal potentials, stable under simulation for a range of out of distribution materials and, upon release, represented a 31% reduction in error over other methods on the Matbench Discovery benchmark. We explore several aspects of foundation model development for materials, with a focus on diffusion pretraining. We evaluate Orb as a model for geometry optimization, Monte Carlo and molecular dynamics simulations.

Band-gap regression with architecture-optimized message-passing neural networks

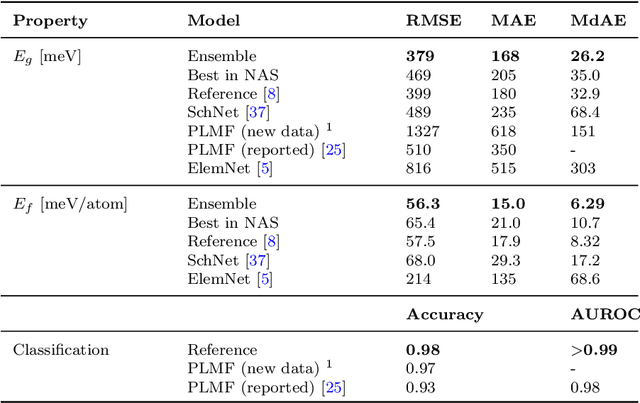
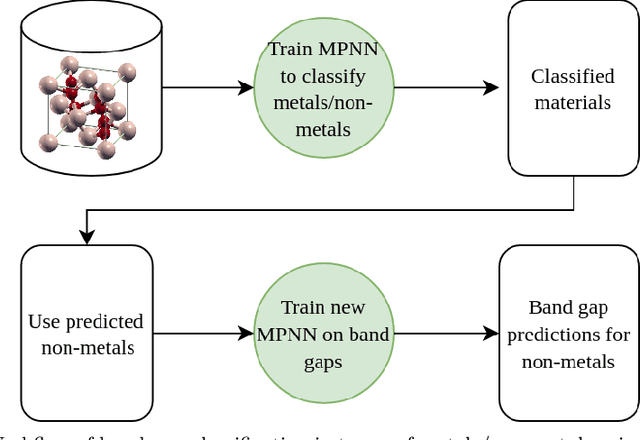
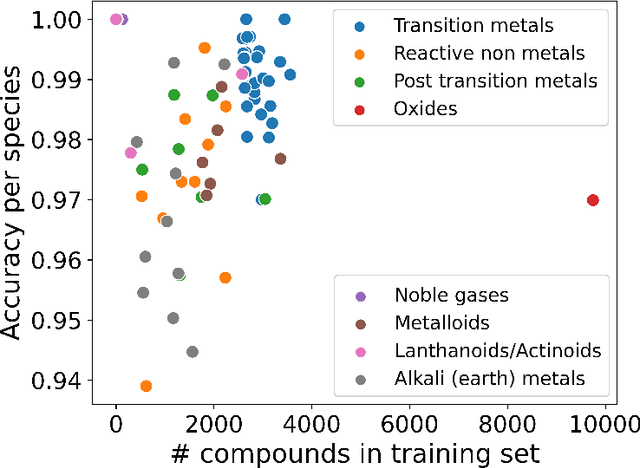
Graph-based neural networks and, specifically, message-passing neural networks (MPNNs) have shown great potential in predicting physical properties of solids. In this work, we train an MPNN to first classify materials through density functional theory data from the AFLOW database as being metallic or semiconducting/insulating. We then perform a neural-architecture search to explore the model architecture and hyperparameter space of MPNNs to predict the band gaps of the materials identified as non-metals. The parameters in the search include the number of message-passing steps, latent size, and activation-function, among others. The top-performing models from the search are pooled into an ensemble that significantly outperforms existing models from the literature. Uncertainty quantification is evaluated with Monte-Carlo Dropout and ensembling, with the ensemble method proving superior. The domain of applicability of the ensemble model is analyzed with respect to the crystal systems, the inclusion of a Hubbard parameter in the density functional calculations, and the atomic species building up the materials.

Learned Force Fields Are Ready For Ground State Catalyst Discovery

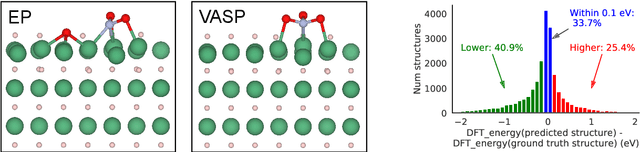
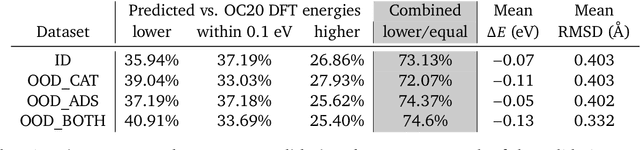
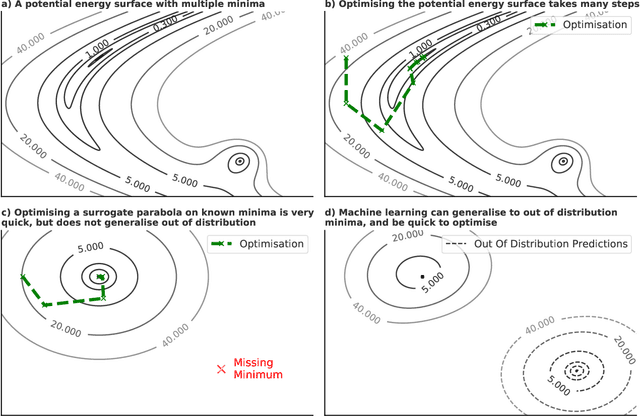
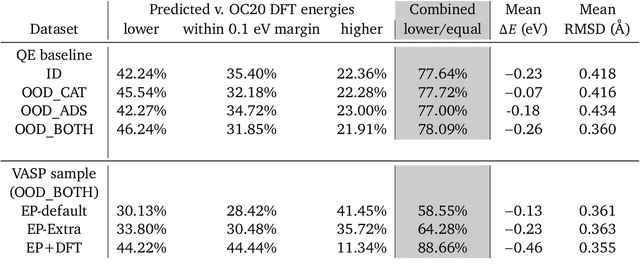
We present evidence that learned density functional theory (``DFT'') force fields are ready for ground state catalyst discovery. Our key finding is that relaxation using forces from a learned potential yields structures with similar or lower energy to those relaxed using the RPBE functional in over 50\% of evaluated systems, despite the fact that the predicted forces differ significantly from the ground truth. This has the surprising implication that learned potentials may be ready for replacing DFT in challenging catalytic systems such as those found in the Open Catalyst 2020 dataset. Furthermore, we show that a force field trained on a locally harmonic energy surface with the same minima as a target DFT energy is also able to find lower or similar energy structures in over 50\% of cases. This ``Easy Potential'' converges in fewer steps than a standard model trained on true energies and forces, which further accelerates calculations. Its success illustrates a key point: learned potentials can locate energy minima even when the model has high force errors. The main requirement for structure optimisation is simply that the learned potential has the correct minima. Since learned potentials are fast and scale linearly with system size, our results open the possibility of quickly finding ground states for large systems.

Pre-training via Denoising for Molecular Property Prediction

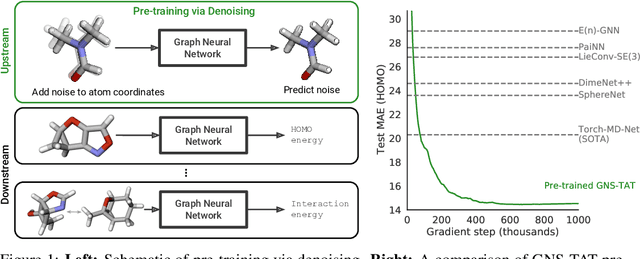
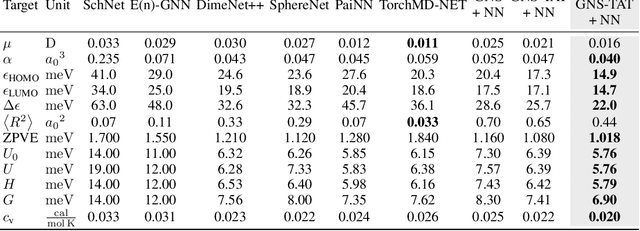
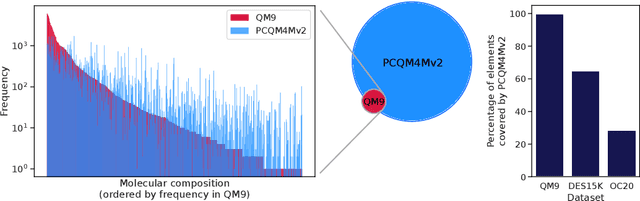
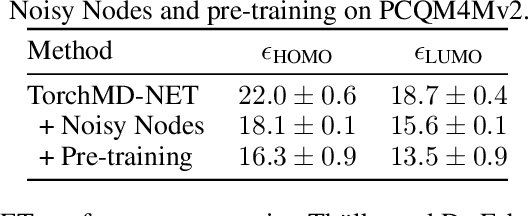
Many important problems involving molecular property prediction from 3D structures have limited data, posing a generalization challenge for neural networks. In this paper, we describe a pre-training technique that utilizes large datasets of 3D molecular structures at equilibrium to learn meaningful representations for downstream tasks. Inspired by recent advances in noise regularization, our pre-training objective is based on denoising. Relying on the well-known link between denoising autoencoders and score-matching, we also show that the objective corresponds to learning a molecular force field -- arising from approximating the physical state distribution with a mixture of Gaussians -- directly from equilibrium structures. Our experiments demonstrate that using this pre-training objective significantly improves performance on multiple benchmarks, achieving a new state-of-the-art on the majority of targets in the widely used QM9 dataset. Our analysis then provides practical insights into the effects of different factors -- dataset sizes, model size and architecture, and the choice of upstream and downstream datasets -- on pre-training.

Learned Coarse Models for Efficient Turbulence Simulation

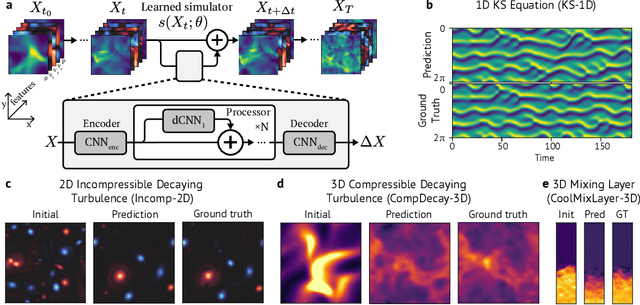
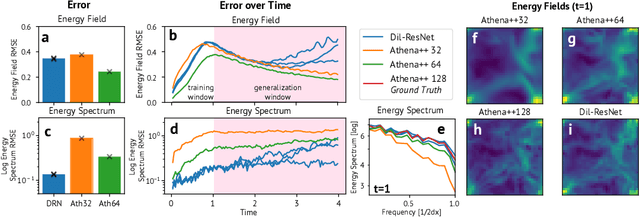
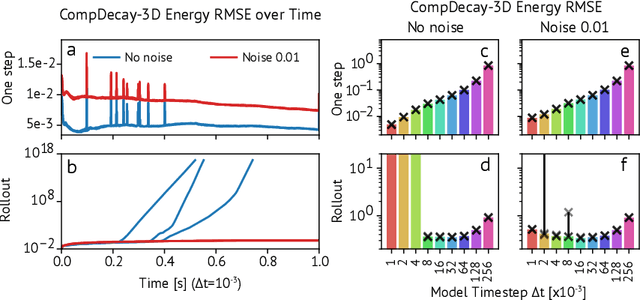
Turbulence simulation with classical numerical solvers requires very high-resolution grids to accurately resolve dynamics. Here we train learned simulators at low spatial and temporal resolutions to capture turbulent dynamics generated at high resolution. We show that our proposed model can simulate turbulent dynamics more accurately than classical numerical solvers at the same low resolutions across various scientifically relevant metrics. Our model is trained end-to-end from data and is capable of learning a range of challenging chaotic and turbulent dynamics at low resolution, including trajectories generated by the state-of-the-art Athena++ engine. We show that our simpler, general-purpose architecture outperforms various more specialized, turbulence-specific architectures from the learned turbulence simulation literature. In general, we see that learned simulators yield unstable trajectories; however, we show that tuning training noise and temporal downsampling solves this problem. We also find that while generalization beyond the training distribution is a challenge for learned models, training noise, convolutional architectures, and added loss constraints can help. Broadly, we conclude that our learned simulator outperforms traditional solvers run on coarser grids, and emphasize that simple design choices can offer stability and robust generalization.

Automap: Towards Ergonomic Automated Parallelism for ML Models

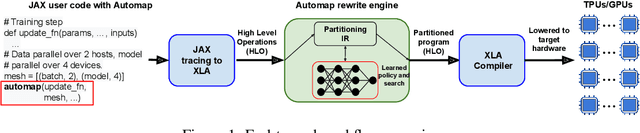
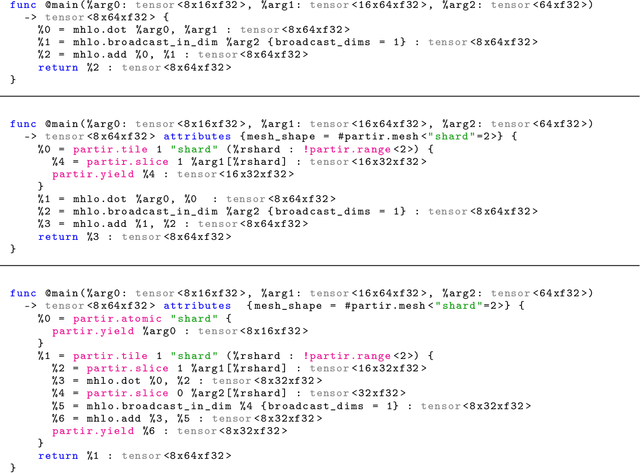
The rapid rise in demand for training large neural network architectures has brought into focus the need for partitioning strategies, for example by using data, model, or pipeline parallelism. Implementing these methods is increasingly supported through program primitives, but identifying efficient partitioning strategies requires expensive experimentation and expertise. We present the prototype of an automated partitioner that seamlessly integrates into existing compilers and existing user workflows. Our partitioner enables SPMD-style parallelism that encompasses data parallelism and parameter/activation sharding. Through a combination of inductive tactics and search in a platform-independent partitioning IR, automap can recover expert partitioning strategies such as Megatron sharding for transformer layers.

Large-scale graph representation learning with very deep GNNs and self-supervision

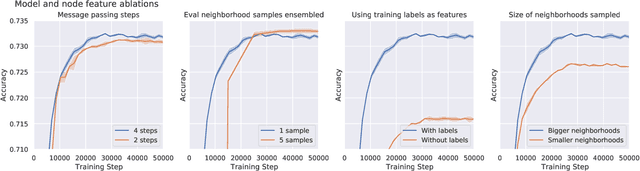
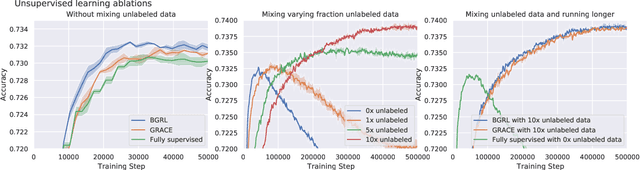
Effectively and efficiently deploying graph neural networks (GNNs) at scale remains one of the most challenging aspects of graph representation learning. Many powerful solutions have only ever been validated on comparatively small datasets, often with counter-intuitive outcomes -- a barrier which has been broken by the Open Graph Benchmark Large-Scale Challenge (OGB-LSC). We entered the OGB-LSC with two large-scale GNNs: a deep transductive node classifier powered by bootstrapping, and a very deep (up to 50-layer) inductive graph regressor regularised by denoising objectives. Our models achieved an award-level (top-3) performance on both the MAG240M and PCQM4M benchmarks. In doing so, we demonstrate evidence of scalable self-supervised graph representation learning, and utility of very deep GNNs -- both very important open issues. Our code is publicly available at: https://github.com/deepmind/deepmind-research/tree/master/ogb_lsc.

Very Deep Graph Neural Networks Via Noise Regularisation

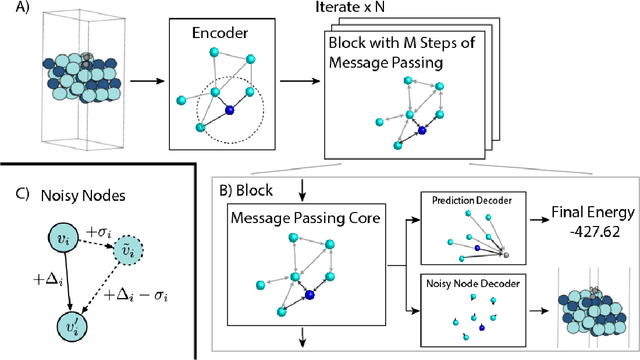
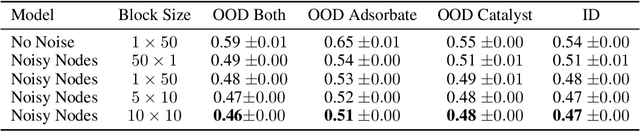
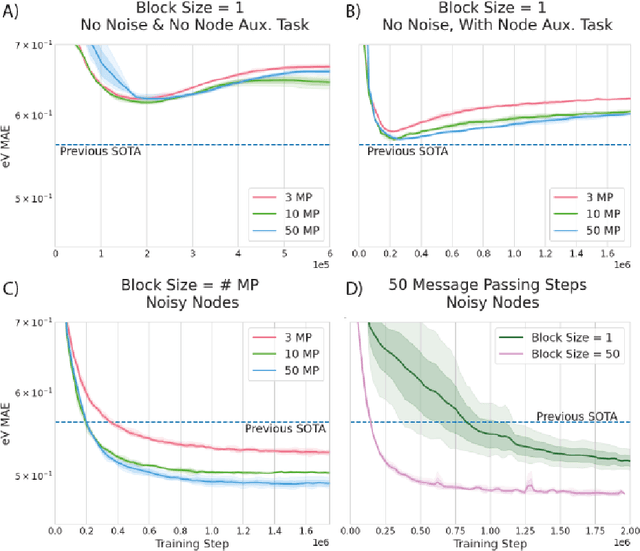
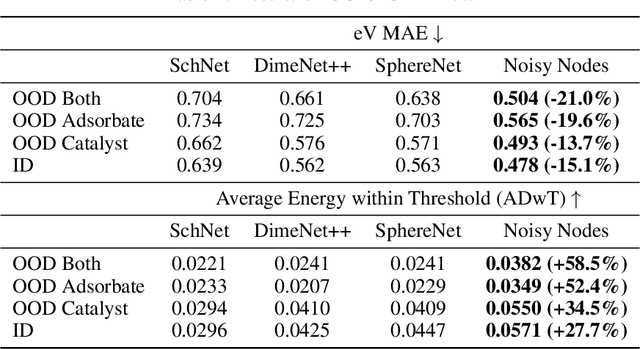
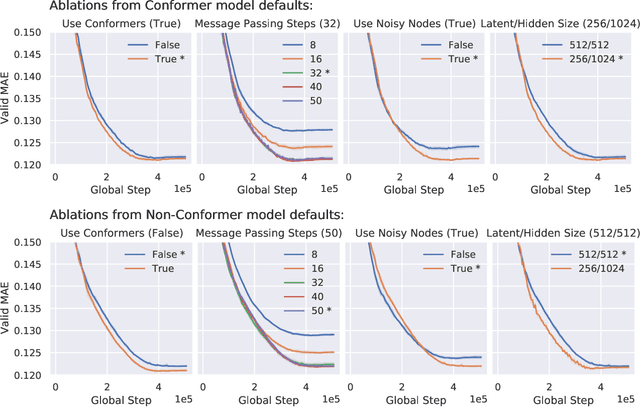
Graph Neural Networks (GNNs) perform learned message passing over an input graph, but conventional wisdom says performing more than handful of steps makes training difficult and does not yield improved performance. Here we show the contrary. We train a deep GNN with up to 100 message passing steps and achieve several state-of-the-art results on two challenging molecular property prediction benchmarks, Open Catalyst 2020 IS2RE and QM9. Our approach depends crucially on a novel but simple regularisation method, which we call ``Noisy Nodes'', in which we corrupt the input graph with noise and add an auxiliary node autoencoder loss if the task is graph property prediction. Our results show this regularisation method allows the model to monotonically improve in performance with increased message passing steps. Our work opens new opportunities for reaping the benefits of deep neural networks in the space of graph and other structured prediction problems.