Analysis of static and dynamic batching algorithms for graph neural networks

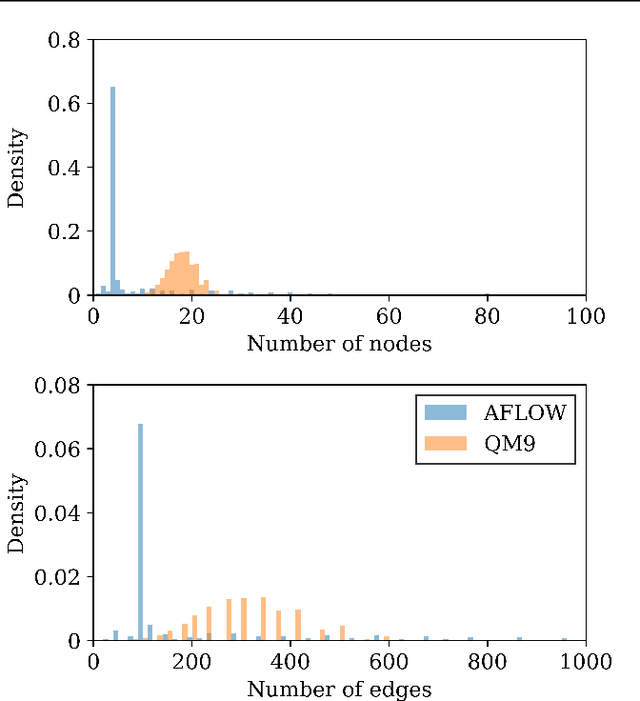
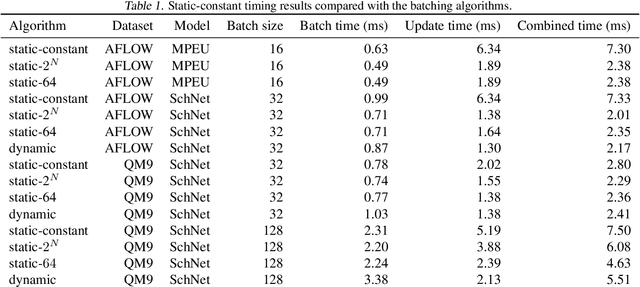
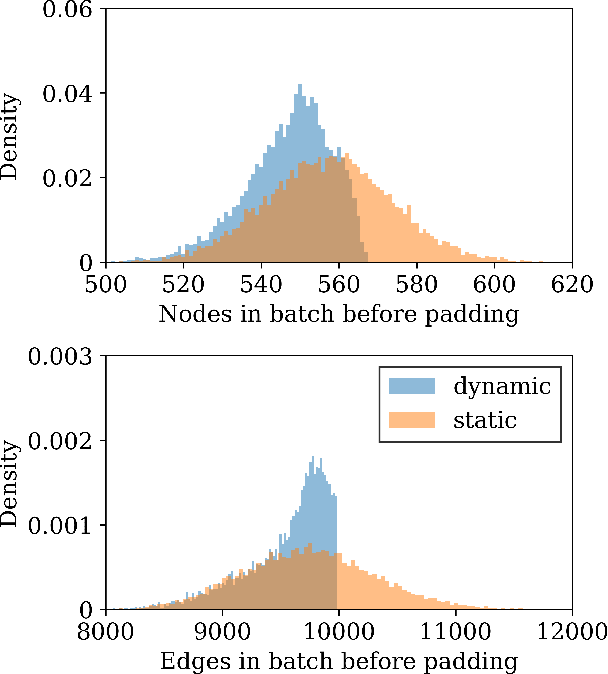
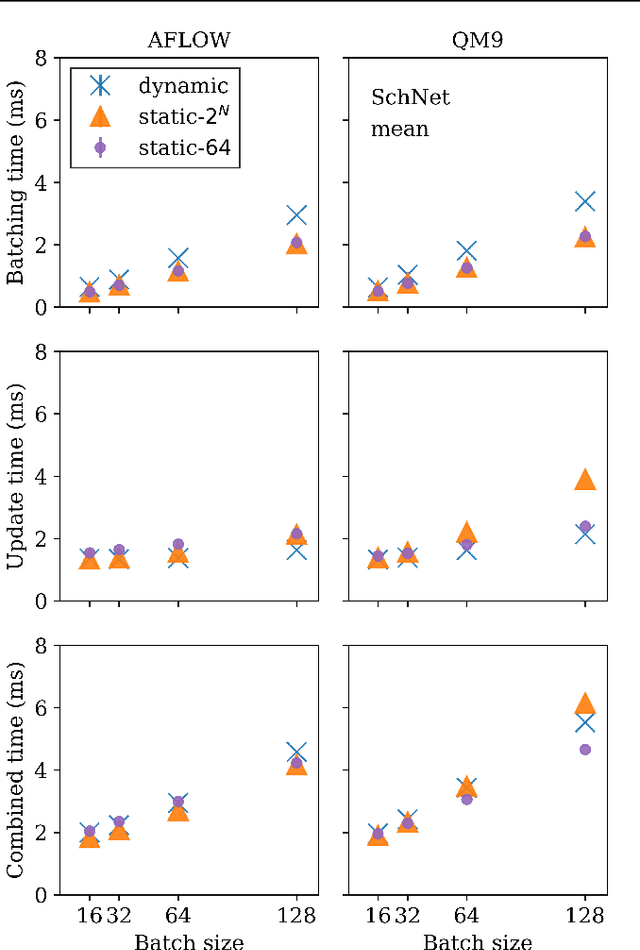
Graph neural networks (GNN) have shown promising results for several domains such as materials science, chemistry, and the social sciences. GNN models often contain millions of parameters, and like other neural network (NN) models, are often fed only a fraction of the graphs that make up the training dataset in batches to update model parameters. The effect of batching algorithms on training time and model performance has been thoroughly explored for NNs but not yet for GNNs. We analyze two different batching algorithms for graph based models, namely static and dynamic batching. We use the Jraph library built on JAX to perform our experiments, where we compare the two batching methods for two datasets, the QM9 dataset of small molecules and the AFLOW materials database. Our experiments show that significant training time savings can be found from changing the batching algorithm, but the fastest algorithm depends on the data, model, batch size and number of training steps run. Experiments show no significant difference in model learning between the algorithms.

How big is Big Data?

Big data has ushered in a new wave of predictive power using machine learning models. In this work, we assess what {\it big} means in the context of typical materials-science machine-learning problems. This concerns not only data volume, but also data quality and veracity as much as infrastructure issues. With selected examples, we ask (i) how models generalize to similar datasets, (ii) how high-quality datasets can be gathered from heterogenous sources, (iii) how the feature set and complexity of a model can affect expressivity, and (iv) what infrastructure requirements are needed to create larger datasets and train models on them. In sum, we find that big data present unique challenges along very different aspects that should serve to motivate further work.

Band-gap regression with architecture-optimized message-passing neural networks

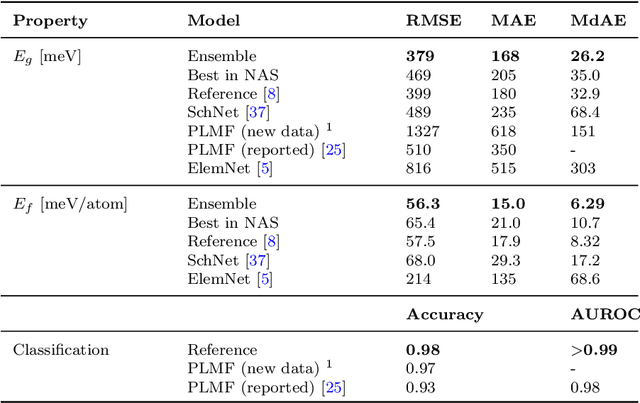
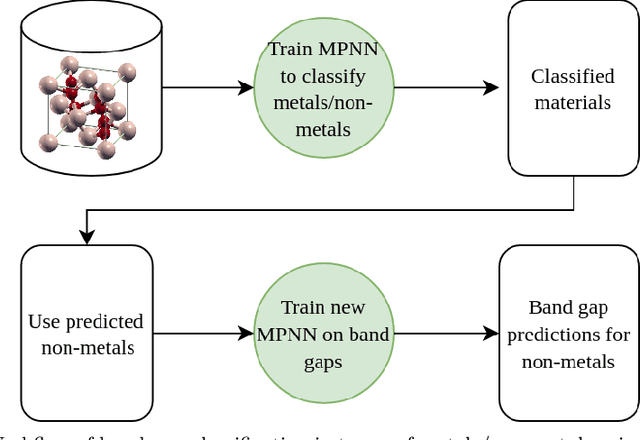
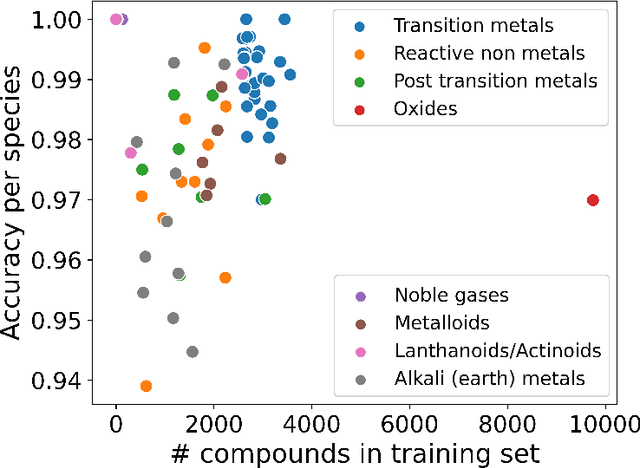
Graph-based neural networks and, specifically, message-passing neural networks (MPNNs) have shown great potential in predicting physical properties of solids. In this work, we train an MPNN to first classify materials through density functional theory data from the AFLOW database as being metallic or semiconducting/insulating. We then perform a neural-architecture search to explore the model architecture and hyperparameter space of MPNNs to predict the band gaps of the materials identified as non-metals. The parameters in the search include the number of message-passing steps, latent size, and activation-function, among others. The top-performing models from the search are pooled into an ensemble that significantly outperforms existing models from the literature. Uncertainty quantification is evaluated with Monte-Carlo Dropout and ensembling, with the ensemble method proving superior. The domain of applicability of the ensemble model is analyzed with respect to the crystal systems, the inclusion of a Hubbard parameter in the density functional calculations, and the atomic species building up the materials.

Extrapolation to complete basis-set limit in density-functional theory by quantile random-forest models

The numerical precision of density-functional-theory (DFT) calculations depends on a variety of computational parameters, one of the most critical being the basis-set size. The ultimate precision is reached with an infinitely large basis set, i.e., in the limit of a complete basis set (CBS). Our aim in this work is to find a machine-learning model that extrapolates finite basis-size calculations to the CBS limit. We start with a data set of 63 binary solids investigated with two all-electron DFT codes, exciting and FHI-aims, which employ very different types of basis sets. A quantile-random-forest model is used to estimate the total-energy correction with respect to a fully converged calculation as a function of the basis-set size. The random-forest model achieves a symmetric mean absolute percentage error of lower than 25% for both codes and outperforms previous approaches in the literature. Our approach also provides prediction intervals, which quantify the uncertainty of the models' predictions.