Accelerating the Training and Improving the Reliability of Machine-Learned Interatomic Potentials for Strongly Anharmonic Materials through Active Learning

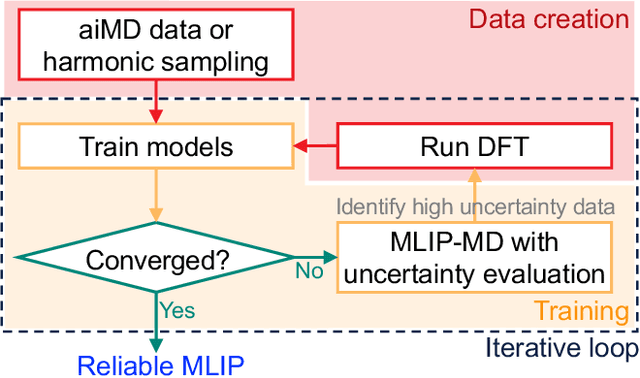
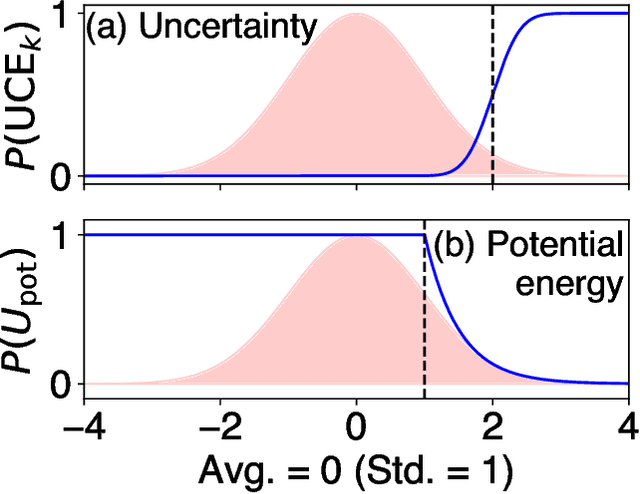
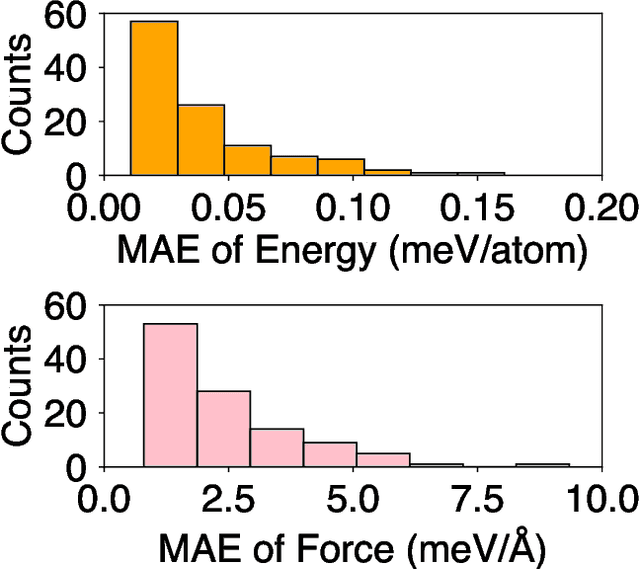
Molecular dynamics (MD) employing machine-learned interatomic potentials (MLIPs) serve as an efficient, urgently needed complement to ab initio molecular dynamics (aiMD). By training these potentials on data generated from ab initio methods, their averaged predictions can exhibit comparable performance to ab initio methods at a fraction of the cost. However, insufficient training sets might lead to an improper description of the dynamics in strongly anharmonic materials, because critical effects might be overlooked in relevant cases, or only incorrectly captured, or hallucinated by the MLIP when they are not actually present. In this work, we show that an active learning scheme that combines MD with MLIPs (MLIP-MD) and uncertainty estimates can avoid such problematic predictions. In short, efficient MLIP-MD is used to explore configuration space quickly, whereby an acquisition function based on uncertainty estimates and on energetic viability is employed to maximize the value of the newly generated data and to focus on the most unfamiliar but reasonably accessible regions of phase space. To verify our methodology, we screen over 112 materials and identify 10 examples experiencing the aforementioned problems. Using CuI and AgGaSe$_2$ as archetypes for these problematic materials, we discuss the physical implications for strongly anharmonic effects and demonstrate how the developed active learning scheme can address these issues.

Extrapolation to complete basis-set limit in density-functional theory by quantile random-forest models

The numerical precision of density-functional-theory (DFT) calculations depends on a variety of computational parameters, one of the most critical being the basis-set size. The ultimate precision is reached with an infinitely large basis set, i.e., in the limit of a complete basis set (CBS). Our aim in this work is to find a machine-learning model that extrapolates finite basis-size calculations to the CBS limit. We start with a data set of 63 binary solids investigated with two all-electron DFT codes, exciting and FHI-aims, which employ very different types of basis sets. A quantile-random-forest model is used to estimate the total-energy correction with respect to a fully converged calculation as a function of the basis-set size. The random-forest model achieves a symmetric mean absolute percentage error of lower than 25% for both codes and outperforms previous approaches in the literature. Our approach also provides prediction intervals, which quantify the uncertainty of the models' predictions.

Heat flux for semi-local machine-learning potentials

The Green-Kubo (GK) method is a rigorous framework for heat transport simulations in materials. However, it requires an accurate description of the potential-energy surface and carefully converged statistics. Machine-learning potentials can achieve the accuracy of first-principles simulations while allowing to reach well beyond their simulation time and length scales at a fraction of the cost. In this paper, we explain how to apply the GK approach to the recent class of message-passing machine-learning potentials, which iteratively consider semi-local interactions beyond the initial interaction cutoff. We derive an adapted heat flux formulation that can be implemented using automatic differentiation without compromising computational efficiency. The approach is demonstrated and validated by calculating the thermal conductivity of zirconium dioxide across temperatures.