Probing the effects of broken symmetries in machine learning

Symmetry is one of the most central concepts in physics, and it is no surprise that it has also been widely adopted as an inductive bias for machine-learning models applied to the physical sciences. This is especially true for models targeting the properties of matter at the atomic scale. Both established and state-of-the-art approaches, with almost no exceptions, are built to be exactly equivariant to translations, permutations, and rotations of the atoms. Incorporating symmetries -- rotations in particular -- constrains the model design space and implies more complicated architectures that are often also computationally demanding. There are indications that non-symmetric models can easily learn symmetries from data, and that doing so can even be beneficial for the accuracy of the model. We put a model that obeys rotational invariance only approximately to the test, in realistic scenarios involving simulations of gas-phase, liquid, and solid water. We focus specifically on physical observables that are likely to be affected -- directly or indirectly -- by symmetry breaking, finding negligible consequences when the model is used in an interpolative, bulk, regime. Even for extrapolative gas-phase predictions, the model remains very stable, even though symmetry artifacts are noticeable. We also discuss strategies that can be used to systematically reduce the magnitude of symmetry breaking when it occurs, and assess their impact on the convergence of observables.

Stress and heat flux via automatic differentiation

Machine-learning potentials provide computationally efficient and accurate approximations of the Born-Oppenheimer potential energy surface. This potential determines many materials properties and simulation techniques usually require its gradients, in particular forces and stress for molecular dynamics, and heat flux for thermal transport properties. Recently developed potentials feature high body order and can include equivariant semi-local interactions through message-passing mechanisms. Due to their complex functional forms, they rely on automatic differentiation (AD), overcoming the need for manual implementations or finite-difference schemes to evaluate gradients. This study demonstrates a unified AD approach to obtain forces, stress, and heat flux for such potentials, and provides a model-independent implementation. The method is tested on the Lennard-Jones potential, and then applied to predict cohesive properties and thermal conductivity of tin selenide using an equivariant message-passing neural network potential.

Heat flux for semi-local machine-learning potentials

The Green-Kubo (GK) method is a rigorous framework for heat transport simulations in materials. However, it requires an accurate description of the potential-energy surface and carefully converged statistics. Machine-learning potentials can achieve the accuracy of first-principles simulations while allowing to reach well beyond their simulation time and length scales at a fraction of the cost. In this paper, we explain how to apply the GK approach to the recent class of message-passing machine-learning potentials, which iteratively consider semi-local interactions beyond the initial interaction cutoff. We derive an adapted heat flux formulation that can be implemented using automatic differentiation without compromising computational efficiency. The approach is demonstrated and validated by calculating the thermal conductivity of zirconium dioxide across temperatures.

Representations of molecules and materials for interpolation of quantum-mechanical simulations via machine learning

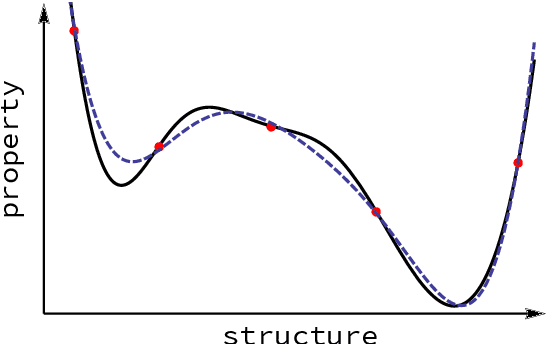
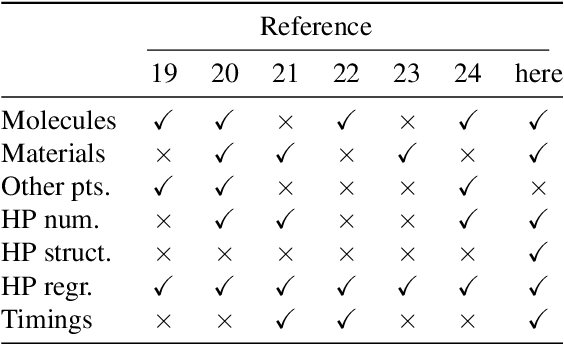
Computational study of molecules and materials from first principles is a cornerstone of physics, chemistry and materials science, but limited by the cost of accurate and precise simulations. In settings involving many simulations, machine learning can reduce these costs, sometimes by orders of magnitude, by interpolating between reference simulations. This requires representations that describe any molecule or material and support interpolation. We review, discuss and benchmark state-of-the-art representations and relations between them, including smooth overlap of atomic positions, many-body tensor representation, and symmetry functions. For this, we use a unified mathematical framework based on many-body functions, group averaging and tensor products, and compare energy predictions for organic molecules, binary alloys and Al-Ga-In sesquioxides in numerical experiments controlled for data distribution, regression method and hyper-parameter optimization.