The Restricted Isometry of ReLU Networks: Generalization through Norm Concentration

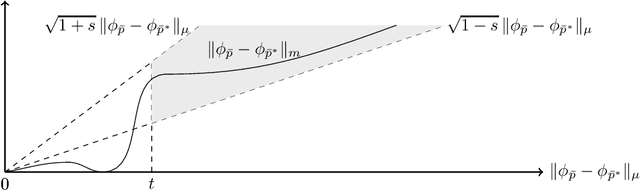
While regression tasks aim at interpolating a relation on the entire input space, they often have to be solved with a limited amount of training data. Still, if the hypothesis functions can be sketched well with the data, one can hope for identifying a generalizing model. In this work, we introduce with the Neural Restricted Isometry Property (NeuRIP) a uniform concentration event, in which all shallow $\mathrm{ReLU}$ networks are sketched with the same quality. To derive the sample complexity for achieving NeuRIP, we bound the covering numbers of the networks in the Sub-Gaussian metric and apply chaining techniques. In case of the NeuRIP event, we then provide bounds on the expected risk, which hold for networks in any sublevel set of the empirical risk. We conclude that all networks with sufficiently small empirical risk generalize uniformly.

Representations of molecules and materials for interpolation of quantum-mechanical simulations via machine learning

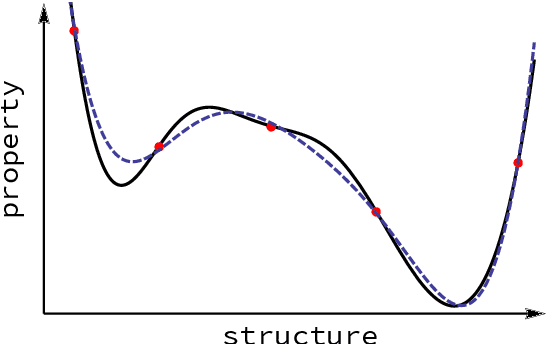
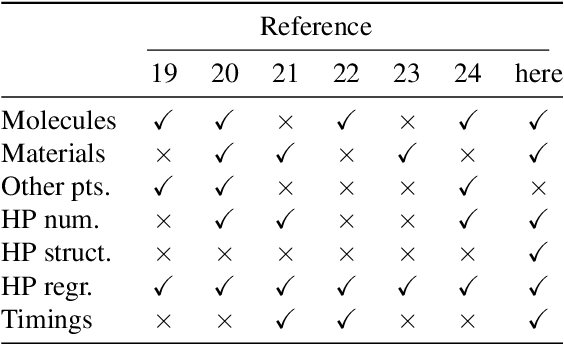
Computational study of molecules and materials from first principles is a cornerstone of physics, chemistry and materials science, but limited by the cost of accurate and precise simulations. In settings involving many simulations, machine learning can reduce these costs, sometimes by orders of magnitude, by interpolating between reference simulations. This requires representations that describe any molecule or material and support interpolation. We review, discuss and benchmark state-of-the-art representations and relations between them, including smooth overlap of atomic positions, many-body tensor representation, and symmetry functions. For this, we use a unified mathematical framework based on many-body functions, group averaging and tensor products, and compare energy predictions for organic molecules, binary alloys and Al-Ga-In sesquioxides in numerical experiments controlled for data distribution, regression method and hyper-parameter optimization.