The Restricted Isometry of ReLU Networks: Generalization through Norm Concentration
Paper and Code
Jul 01, 2020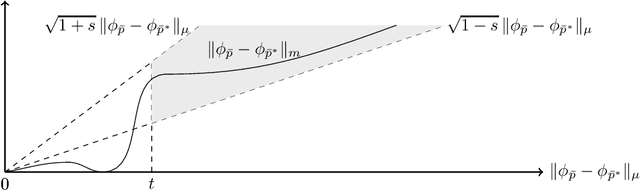
While regression tasks aim at interpolating a relation on the entire input space, they often have to be solved with a limited amount of training data. Still, if the hypothesis functions can be sketched well with the data, one can hope for identifying a generalizing model. In this work, we introduce with the Neural Restricted Isometry Property (NeuRIP) a uniform concentration event, in which all shallow $\mathrm{ReLU}$ networks are sketched with the same quality. To derive the sample complexity for achieving NeuRIP, we bound the covering numbers of the networks in the Sub-Gaussian metric and apply chaining techniques. In case of the NeuRIP event, we then provide bounds on the expected risk, which hold for networks in any sublevel set of the empirical risk. We conclude that all networks with sufficiently small empirical risk generalize uniformly.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge