Probing the effects of broken symmetries in machine learning

Symmetry is one of the most central concepts in physics, and it is no surprise that it has also been widely adopted as an inductive bias for machine-learning models applied to the physical sciences. This is especially true for models targeting the properties of matter at the atomic scale. Both established and state-of-the-art approaches, with almost no exceptions, are built to be exactly equivariant to translations, permutations, and rotations of the atoms. Incorporating symmetries -- rotations in particular -- constrains the model design space and implies more complicated architectures that are often also computationally demanding. There are indications that non-symmetric models can easily learn symmetries from data, and that doing so can even be beneficial for the accuracy of the model. We put a model that obeys rotational invariance only approximately to the test, in realistic scenarios involving simulations of gas-phase, liquid, and solid water. We focus specifically on physical observables that are likely to be affected -- directly or indirectly -- by symmetry breaking, finding negligible consequences when the model is used in an interpolative, bulk, regime. Even for extrapolative gas-phase predictions, the model remains very stable, even though symmetry artifacts are noticeable. We also discuss strategies that can be used to systematically reduce the magnitude of symmetry breaking when it occurs, and assess their impact on the convergence of observables.

Smooth, exact rotational symmetrization for deep learning on point clouds

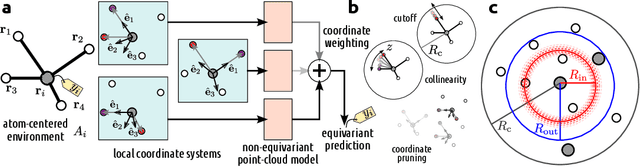
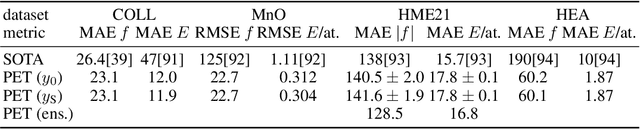
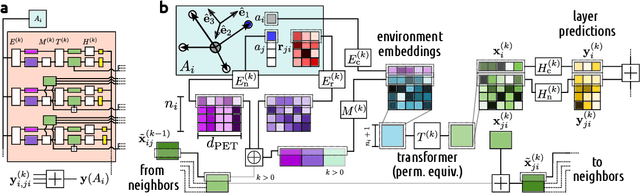
Point clouds are versatile representations of 3D objects and have found widespread application in science and engineering. Many successful deep-learning models have been proposed that use them as input. Some application domains require incorporating exactly physical constraints, including chemical and materials modeling which we focus on in this paper. These constraints include smoothness, and symmetry with respect to translations, rotations, and permutations of identical particles. Most existing architectures in other domains do not fulfill simultaneously all of these requirements and thus are not applicable to atomic-scale simulations. Many of them, however, can be straightforwardly made to incorporate all the physical constraints except for rotational symmetry. We propose a general symmetrization protocol that adds rotational equivariance to any given model while preserving all the other constraints. As a demonstration of the potential of this idea, we introduce the Point Edge Transformer (PET) architecture, which is not intrinsically equivariant but achieves state-of-the-art performance on several benchmark datasets of molecules and solids. A-posteriori application of our general protocol makes PET exactly equivariant, with minimal changes to its accuracy. By alleviating the need to explicitly incorporate rotational symmetry within the model, our method bridges the gap between the approaches used in different communities, and simplifies the design of deep-learning schemes for chemical and materials modeling.

Wigner kernels: body-ordered equivariant machine learning without a basis

Machine-learning models based on a point-cloud representation of a physical object are ubiquitous in scientific applications and particularly well-suited to the atomic-scale description of molecules and materials. Among the many different approaches that have been pursued, the description of local atomic environments in terms of their neighbor densities has been used widely and very succesfully. We propose a novel density-based method which involves computing ``Wigner kernels''. These are fully equivariant and body-ordered kernels that can be computed iteratively with a cost that is independent of the radial-chemical basis and grows only linearly with the maximum body-order considered. This is in marked contrast to feature-space models, which comprise an exponentially-growing number of terms with increasing order of correlations. We present several examples of the accuracy of models based on Wigner kernels in chemical applications, for both scalar and tensorial targets, reaching state-of-the-art accuracy on the popular QM9 benchmark dataset, and we discuss the broader relevance of these ideas to equivariant geometric machine-learning.

Completeness of Atomic Structure Representations

Achieving a complete and symmetric description of a group of point particles, such as atoms in a molecule, is a common problem in physics and theoretical chemistry. The introduction of machine learning to science has made this issue even more critical, as it underpins the ability of a model to reproduce arbitrary physical relationships, and to do so while being consistent with basic symmetries and conservation laws. However, the descriptors that are commonly used to represent point clouds -- most notably those adopted to describe matter at the atomic scale -- are unable to distinguish between special arrangements of particles. This makes it impossible to machine learn their properties. Frameworks that are provably complete exist, but are only so in the limit in which they simultaneously describe the mutual relationship between all atoms, which is impractical. We introduce, and demonstrate on a particularly insidious class of atomic arrangements, a strategy to build descriptors that rely solely on information on the relative arrangement of triplets of particles, but can be used to construct symmetry-adapted models that have universal approximation power.

Incompleteness of graph convolutional neural networks for points clouds in three dimensions

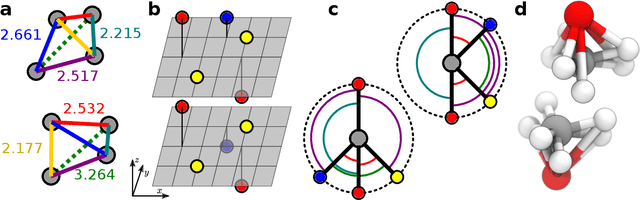
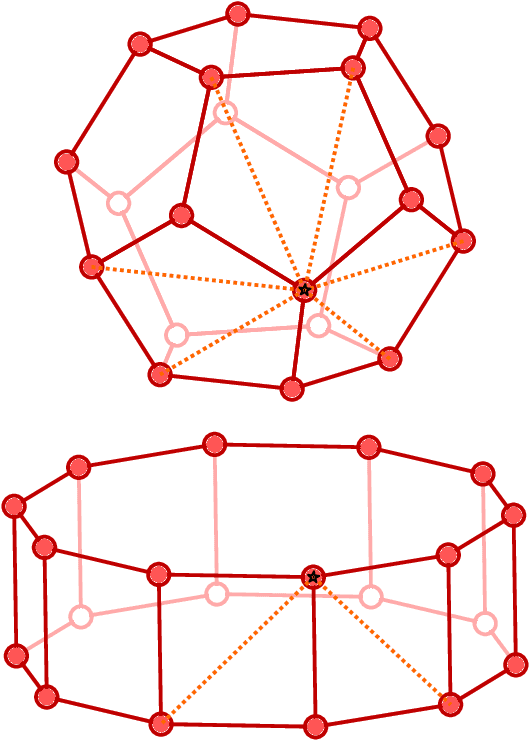
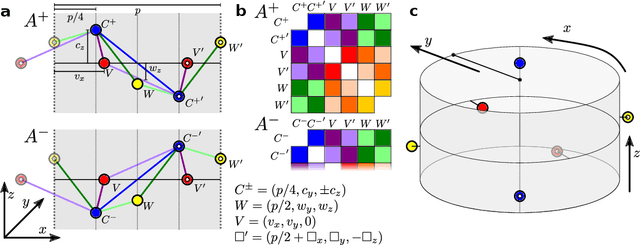
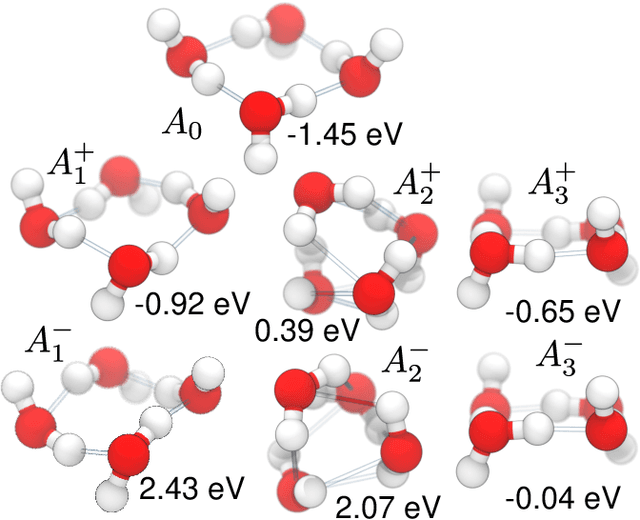
Graph convolutional neural networks (GCNN) are very popular methods in machine learning and have been applied very successfully to the prediction of the properties of molecules and materials. First-order GCNNs are well known to be incomplete, i.e., there exist graphs that are distinct but appear identical when seen through the lens of the GCNN. More complicated schemes have thus been designed to increase their resolving power. Applications to molecules (and more generally, point clouds), however, add a geometric dimension to the problem. The most straightforward and prevalent approach to construct graph representation for the molecules regards atoms as vertices in a graph and draws a bond between each pair of atoms within a certain preselected cutoff. Bonds can be decorated with the distance between atoms, and the resulting "distance graph convolution NNs" (dGCNN) have empirically demonstrated excellent resolving power and are widely used in chemical ML. Here we show that even for the restricted case of graphs induced by 3D atom clouds dGCNNs are not complete. We construct pairs of distinct point clouds that generate graphs that, for any cutoff radius, are equivalent based on a first-order Weisfeiler-Lehman test. This class of degenerate structures includes chemically-plausible configurations, setting an ultimate limit to the expressive power of some of the well-established GCNN architectures for atomistic machine learning. Models that explicitly use angular information in the description of atomic environments can resolve these degeneracies.