Incompleteness of graph convolutional neural networks for points clouds in three dimensions
Paper and Code
Jan 18, 2022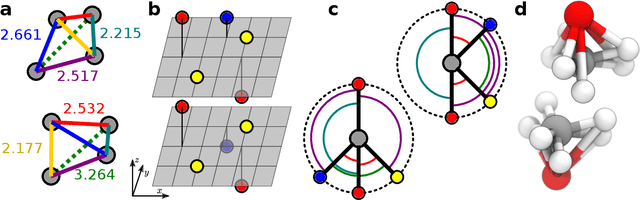
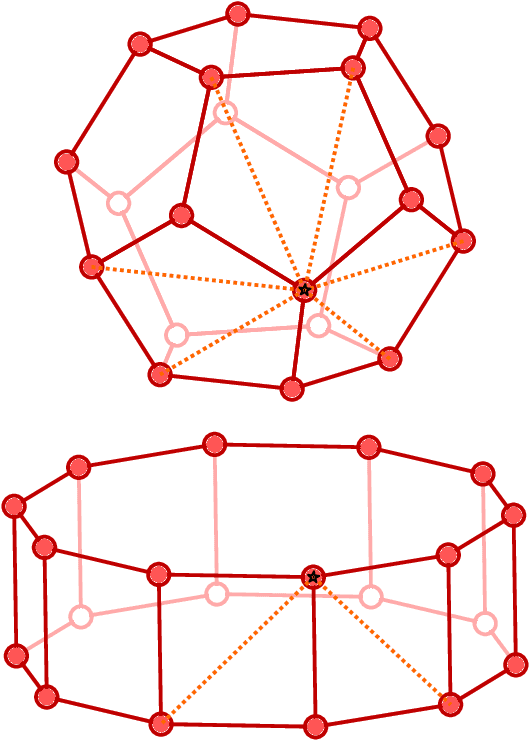
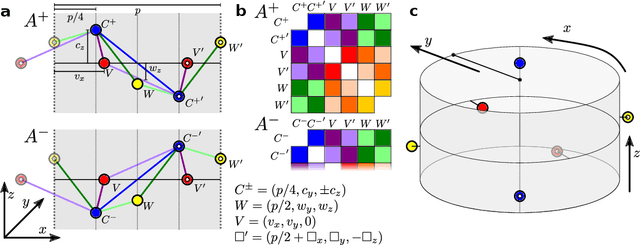
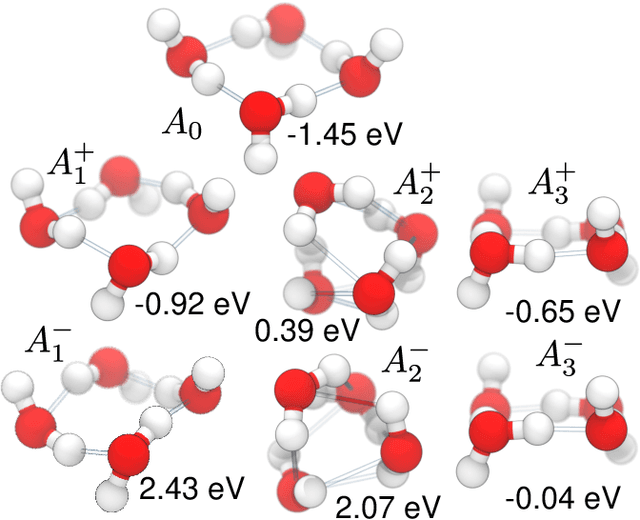
Graph convolutional neural networks (GCNN) are very popular methods in machine learning and have been applied very successfully to the prediction of the properties of molecules and materials. First-order GCNNs are well known to be incomplete, i.e., there exist graphs that are distinct but appear identical when seen through the lens of the GCNN. More complicated schemes have thus been designed to increase their resolving power. Applications to molecules (and more generally, point clouds), however, add a geometric dimension to the problem. The most straightforward and prevalent approach to construct graph representation for the molecules regards atoms as vertices in a graph and draws a bond between each pair of atoms within a certain preselected cutoff. Bonds can be decorated with the distance between atoms, and the resulting "distance graph convolution NNs" (dGCNN) have empirically demonstrated excellent resolving power and are widely used in chemical ML. Here we show that even for the restricted case of graphs induced by 3D atom clouds dGCNNs are not complete. We construct pairs of distinct point clouds that generate graphs that, for any cutoff radius, are equivalent based on a first-order Weisfeiler-Lehman test. This class of degenerate structures includes chemically-plausible configurations, setting an ultimate limit to the expressive power of some of the well-established GCNN architectures for atomistic machine learning. Models that explicitly use angular information in the description of atomic environments can resolve these degeneracies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge