Michele Ceriotti
FlashMD: long-stride, universal prediction of molecular dynamics
May 25, 2025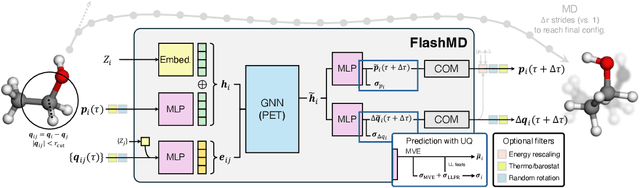
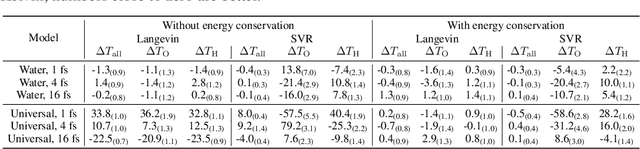
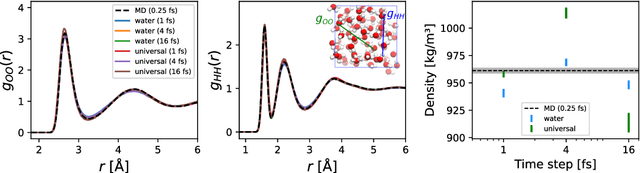
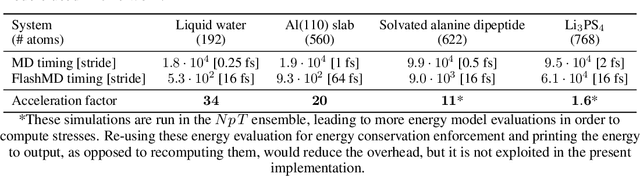
Abstract:Molecular dynamics (MD) provides insights into atomic-scale processes by integrating over time the equations that describe the motion of atoms under the action of interatomic forces. Machine learning models have substantially accelerated MD by providing inexpensive predictions of the forces, but they remain constrained to minuscule time integration steps, which are required by the fast time scale of atomic motion. In this work, we propose FlashMD, a method to predict the evolution of positions and momenta over strides that are between one and two orders of magnitude longer than typical MD time steps. We incorporate considerations on the mathematical and physical properties of Hamiltonian dynamics in the architecture, generalize the approach to allow the simulation of any thermodynamic ensemble, and carefully assess the possible failure modes of such a long-stride MD approach. We validate FlashMD's accuracy in reproducing equilibrium and time-dependent properties, using both system-specific and general-purpose models, extending the ability of MD simulation to reach the long time scales needed to model microscopic processes of high scientific and technological relevance.
Representing spherical tensors with scalar-based machine-learning models
May 08, 2025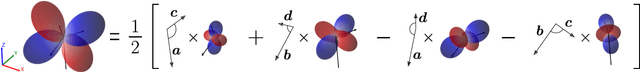
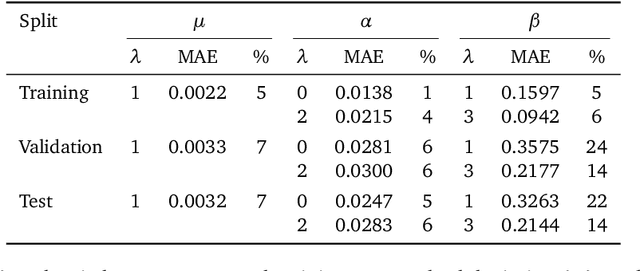
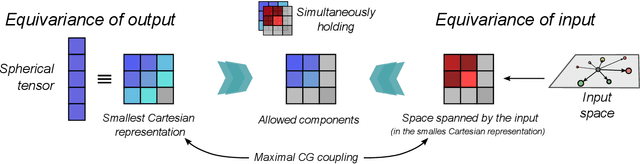
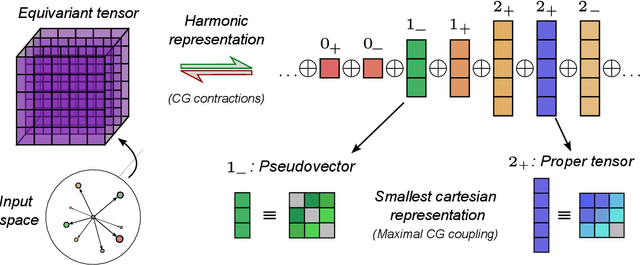
Abstract:Rotational symmetry plays a central role in physics, providing an elegant framework to describe how the properties of 3D objects -- from atoms to the macroscopic scale -- transform under the action of rigid rotations. Equivariant models of 3D point clouds are able to approximate structure-property relations in a way that is fully consistent with the structure of the rotation group, by combining intermediate representations that are themselves spherical tensors. The symmetry constraints however make this approach computationally demanding and cumbersome to implement, which motivates increasingly popular unconstrained architectures that learn approximate symmetries as part of the training process. In this work, we explore a third route to tackle this learning problem, where equivariant functions are expressed as the product of a scalar function of the point cloud coordinates and a small basis of tensors with the appropriate symmetry. We also propose approximations of the general expressions that, while lacking universal approximation properties, are fast, simple to implement, and accurate in practical settings.
PET-MAD, a universal interatomic potential for advanced materials modeling
Mar 18, 2025



Abstract:Machine-learning interatomic potentials (MLIPs) have greatly extended the reach of atomic-scale simulations, offering the accuracy of first-principles calculations at a fraction of the effort. Leveraging large quantum mechanical databases and expressive architectures, recent "universal" models deliver qualitative accuracy across the periodic table but are often biased toward low-energy configurations. We introduce PET-MAD, a generally applicable MLIP trained on a dataset combining stable inorganic and organic solids, systematically modified to enhance atomic diversity. Using a moderate but highly-consistent level of electronic-structure theory, we assess PET-MAD's accuracy on established benchmarks and advanced simulations of six materials. PET-MAD rivals state-of-the-art MLIPs for inorganic solids, while also being reliable for molecules, organic materials, and surfaces. It is stable and fast, enabling, out-of-the-box, the near-quantitative study of thermal and quantum mechanical fluctuations, functional properties, and phase transitions. It can be efficiently fine-tuned to deliver full quantum mechanical accuracy with a minimal number of targeted calculations.
The dark side of the forces: assessing non-conservative force models for atomistic machine learning
Dec 16, 2024



Abstract:The use of machine learning to estimate the energy of a group of atoms, and the forces that drive them to more stable configurations, have revolutionized the fields of computational chemistry and materials discovery. In this domain, rigorous enforcement of symmetry and conservation laws has traditionally been considered essential. For this reason, interatomic forces are usually computed as the derivatives of the potential energy, ensuring energy conservation. Several recent works have questioned this physically-constrained approach, suggesting that using the forces as explicit learning targets yields a better trade-off between accuracy and computational efficiency - and that energy conservation can be learned during training. The present work investigates the applicability of such non-conservative models in microscopic simulations. We identify and demonstrate several fundamental issues, from ill-defined convergence of geometry optimization to instability in various types of molecular dynamics. Contrary to the case of rotational symmetry, lack of energy conservation is hard to learn, control, and correct. The best approach to exploit the acceleration afforded by direct force evaluation might be to use it in tandem with a conservative model, reducing - rather than eliminating - the additional cost of backpropagation, but avoiding most of the pathological behavior associated with non-conservative forces.
Could ChatGPT get an Engineering Degree? Evaluating Higher Education Vulnerability to AI Assistants
Aug 07, 2024
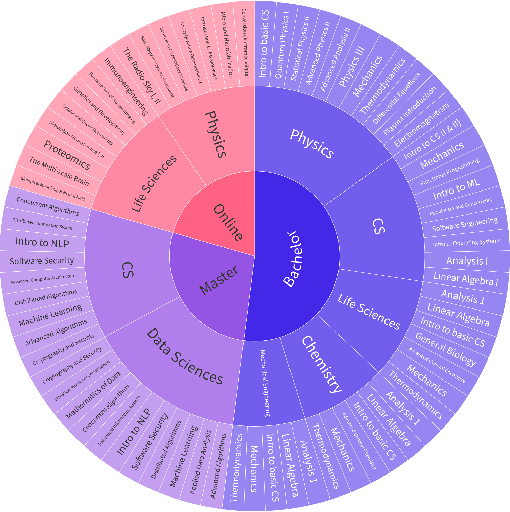
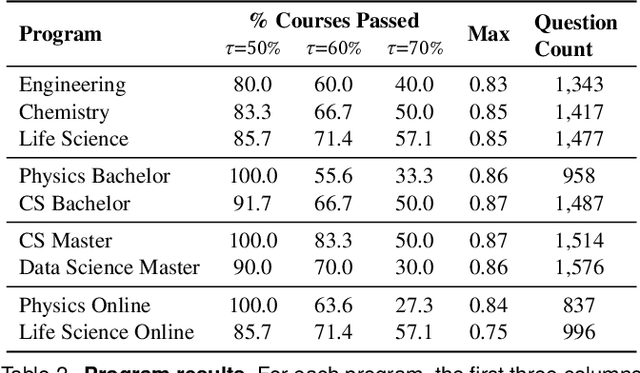

Abstract:AI assistants are being increasingly used by students enrolled in higher education institutions. While these tools provide opportunities for improved teaching and education, they also pose significant challenges for assessment and learning outcomes. We conceptualize these challenges through the lens of vulnerability, the potential for university assessments and learning outcomes to be impacted by student use of generative AI. We investigate the potential scale of this vulnerability by measuring the degree to which AI assistants can complete assessment questions in standard university-level STEM courses. Specifically, we compile a novel dataset of textual assessment questions from 50 courses at EPFL and evaluate whether two AI assistants, GPT-3.5 and GPT-4 can adequately answer these questions. We use eight prompting strategies to produce responses and find that GPT-4 answers an average of 65.8% of questions correctly, and can even produce the correct answer across at least one prompting strategy for 85.1% of questions. When grouping courses in our dataset by degree program, these systems already pass non-project assessments of large numbers of core courses in various degree programs, posing risks to higher education accreditation that will be amplified as these models improve. Our results call for revising program-level assessment design in higher education in light of advances in generative AI.
Probing the effects of broken symmetries in machine learning
Jun 25, 2024Abstract:Symmetry is one of the most central concepts in physics, and it is no surprise that it has also been widely adopted as an inductive bias for machine-learning models applied to the physical sciences. This is especially true for models targeting the properties of matter at the atomic scale. Both established and state-of-the-art approaches, with almost no exceptions, are built to be exactly equivariant to translations, permutations, and rotations of the atoms. Incorporating symmetries -- rotations in particular -- constrains the model design space and implies more complicated architectures that are often also computationally demanding. There are indications that non-symmetric models can easily learn symmetries from data, and that doing so can even be beneficial for the accuracy of the model. We put a model that obeys rotational invariance only approximately to the test, in realistic scenarios involving simulations of gas-phase, liquid, and solid water. We focus specifically on physical observables that are likely to be affected -- directly or indirectly -- by symmetry breaking, finding negligible consequences when the model is used in an interpolative, bulk, regime. Even for extrapolative gas-phase predictions, the model remains very stable, even though symmetry artifacts are noticeable. We also discuss strategies that can be used to systematically reduce the magnitude of symmetry breaking when it occurs, and assess their impact on the convergence of observables.
A prediction rigidity formalism for low-cost uncertainties in trained neural networks
Mar 04, 2024Abstract:Regression methods are fundamental for scientific and technological applications. However, fitted models can be highly unreliable outside of their training domain, and hence the quantification of their uncertainty is crucial in many of their applications. Based on the solution of a constrained optimization problem, we propose "prediction rigidities" as a method to obtain uncertainties of arbitrary pre-trained regressors. We establish a strong connection between our framework and Bayesian inference, and we develop a last-layer approximation that allows the new method to be applied to neural networks. This extension affords cheap uncertainties without any modification to the neural network itself or its training procedure. We show the effectiveness of our method on a wide range of regression tasks, ranging from simple toy models to applications in chemistry and meteorology.
Electronic excited states from physically-constrained machine learning
Nov 08, 2023



Abstract:Data-driven techniques are increasingly used to replace electronic-structure calculations of matter. In this context, a relevant question is whether machine learning (ML) should be applied directly to predict the desired properties or be combined explicitly with physically-grounded operations. We present an example of an integrated modeling approach, in which a symmetry-adapted ML model of an effective Hamiltonian is trained to reproduce electronic excitations from a quantum-mechanical calculation. The resulting model can make predictions for molecules that are much larger and more complex than those that it is trained on, and allows for dramatic computational savings by indirectly targeting the outputs of well-converged calculations while using a parameterization corresponding to a minimal atom-centered basis. These results emphasize the merits of intertwining data-driven techniques with physical approximations, improving the transferability and interpretability of ML models without affecting their accuracy and computational efficiency, and providing a blueprint for developing ML-augmented electronic-structure methods.
Physics-inspired Equivariant Descriptors of Non-bonded Interactions
Aug 25, 2023Abstract:Most of the existing machine-learning schemes applied to atomic-scale simulations rely on a local description of the geometry of a structure, and struggle to model effects that are driven by long-range physical interactions. Efforts to overcome these limitations have focused on the direct incorporation of electrostatics, which is the most prominent effect, often relying on architectures that mirror the functional form of explicit physical models. Including other forms of non-bonded interactions, or predicting properties other than the interatomic potential, requires ad hoc modifications. We propose an alternative approach that extends the long-distance equivariant (LODE) framework to generate local descriptors of an atomic environment that resemble non-bonded potentials with arbitrary asymptotic behaviors, ranging from point-charge electrostatics to dispersion forces. We show that the LODE formalism is amenable to a direct physical interpretation in terms of a generalized multipole expansion, that simplifies its implementation and reduces the number of descriptors needed to capture a given asymptotic behavior. These generalized LODE features provide improved extrapolation capabilities when trained on structures dominated by a given asymptotic behavior, but do not help in capturing the wildly different energy scales that are relevant for a more heterogeneous data set. This approach provides a practical scheme to incorporate different types of non-bonded interactions, and a framework to investigate the interplay of physical and data-related considerations that underlie this challenging modeling problem.
Smooth, exact rotational symmetrization for deep learning on point clouds
May 30, 2023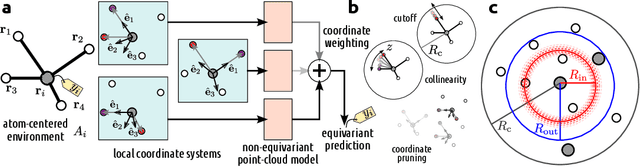
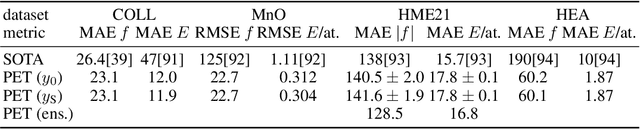
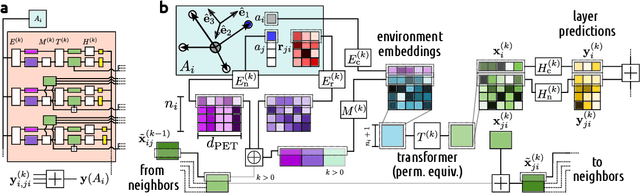

Abstract:Point clouds are versatile representations of 3D objects and have found widespread application in science and engineering. Many successful deep-learning models have been proposed that use them as input. Some application domains require incorporating exactly physical constraints, including chemical and materials modeling which we focus on in this paper. These constraints include smoothness, and symmetry with respect to translations, rotations, and permutations of identical particles. Most existing architectures in other domains do not fulfill simultaneously all of these requirements and thus are not applicable to atomic-scale simulations. Many of them, however, can be straightforwardly made to incorporate all the physical constraints except for rotational symmetry. We propose a general symmetrization protocol that adds rotational equivariance to any given model while preserving all the other constraints. As a demonstration of the potential of this idea, we introduce the Point Edge Transformer (PET) architecture, which is not intrinsically equivariant but achieves state-of-the-art performance on several benchmark datasets of molecules and solids. A-posteriori application of our general protocol makes PET exactly equivariant, with minimal changes to its accuracy. By alleviating the need to explicitly incorporate rotational symmetry within the model, our method bridges the gap between the approaches used in different communities, and simplifies the design of deep-learning schemes for chemical and materials modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge