Lookup multivariate Kolmogorov-Arnold Networks

High-dimensional linear mappings, or linear layers, dominate both the parameter count and the computational cost of most modern deep-learning models. We introduce a general drop-in replacement, lookup multivariate Kolmogorov-Arnold Networks (lmKANs), which deliver a substantially better trade-off between capacity and inference cost. Our construction expresses a general high-dimensional mapping through trainable low-dimensional multivariate functions. These functions can carry dozens or hundreds of trainable parameters each, and yet it takes only a few multiplications to compute them because they are implemented as spline lookup tables. Empirically, lmKANs reduce inference FLOPs by up to 6.0x while matching the flexibility of MLPs in general high-dimensional function approximation. In another feedforward fully connected benchmark, on the tabular-like dataset of randomly displaced methane configurations, lmKANs enable more than 10x higher H100 throughput at equal accuracy. Within frameworks of Convolutional Neural Networks, lmKAN-based CNNs cut inference FLOPs at matched accuracy by 1.6-2.1x and by 1.7x on the CIFAR-10 and ImageNet-1k datasets, respectively. Our code, including dedicated CUDA kernels, is available online at https://github.com/schwallergroup/lmkan.

PET-MAD, a universal interatomic potential for advanced materials modeling

Machine-learning interatomic potentials (MLIPs) have greatly extended the reach of atomic-scale simulations, offering the accuracy of first-principles calculations at a fraction of the effort. Leveraging large quantum mechanical databases and expressive architectures, recent "universal" models deliver qualitative accuracy across the periodic table but are often biased toward low-energy configurations. We introduce PET-MAD, a generally applicable MLIP trained on a dataset combining stable inorganic and organic solids, systematically modified to enhance atomic diversity. Using a moderate but highly-consistent level of electronic-structure theory, we assess PET-MAD's accuracy on established benchmarks and advanced simulations of six materials. PET-MAD rivals state-of-the-art MLIPs for inorganic solids, while also being reliable for molecules, organic materials, and surfaces. It is stable and fast, enabling, out-of-the-box, the near-quantitative study of thermal and quantum mechanical fluctuations, functional properties, and phase transitions. It can be efficiently fine-tuned to deliver full quantum mechanical accuracy with a minimal number of targeted calculations.

Optimal radial basis for density-based atomic representations

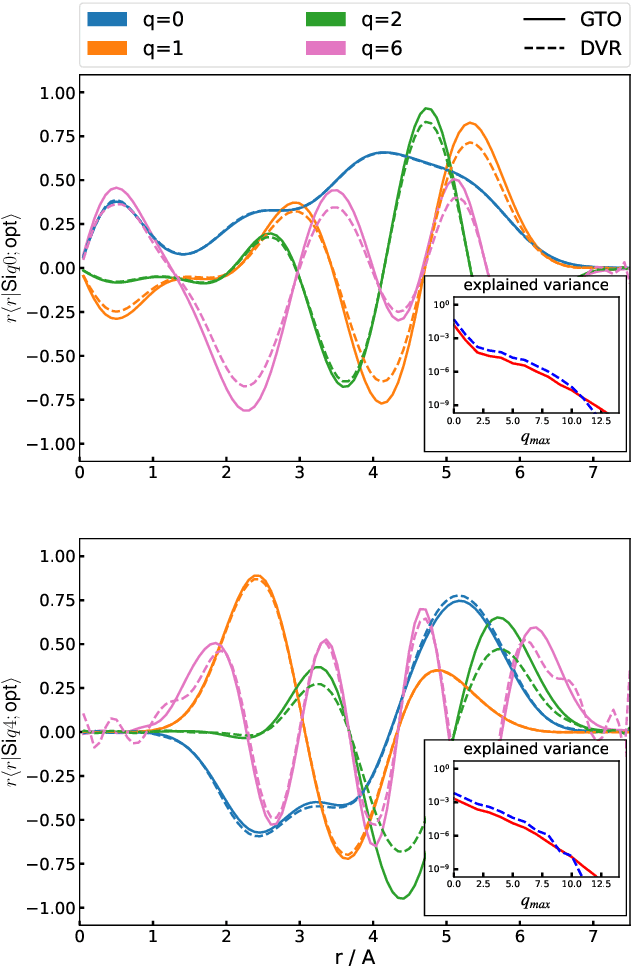
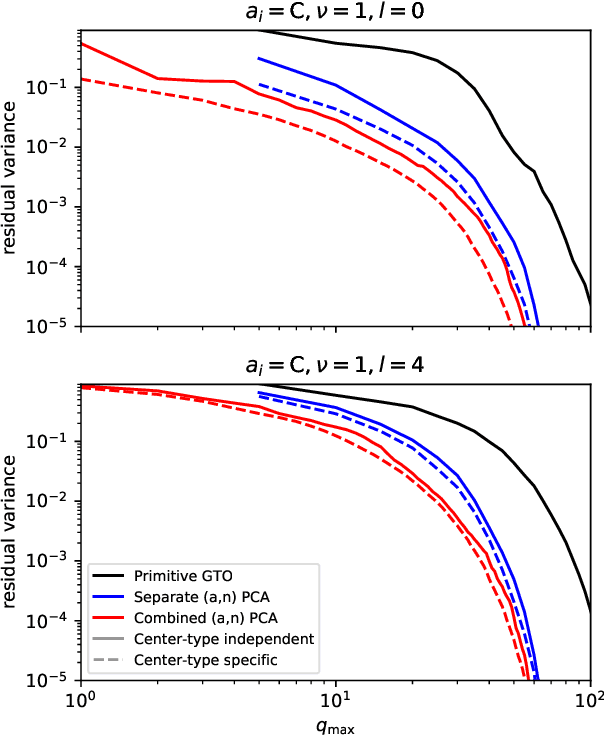
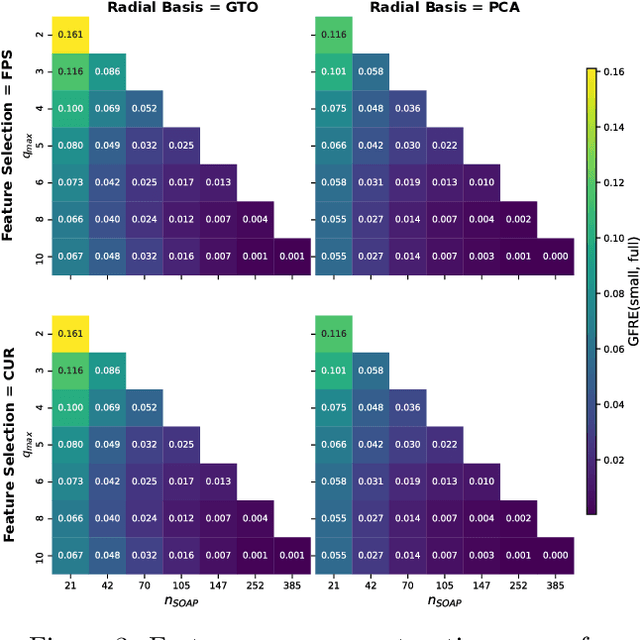
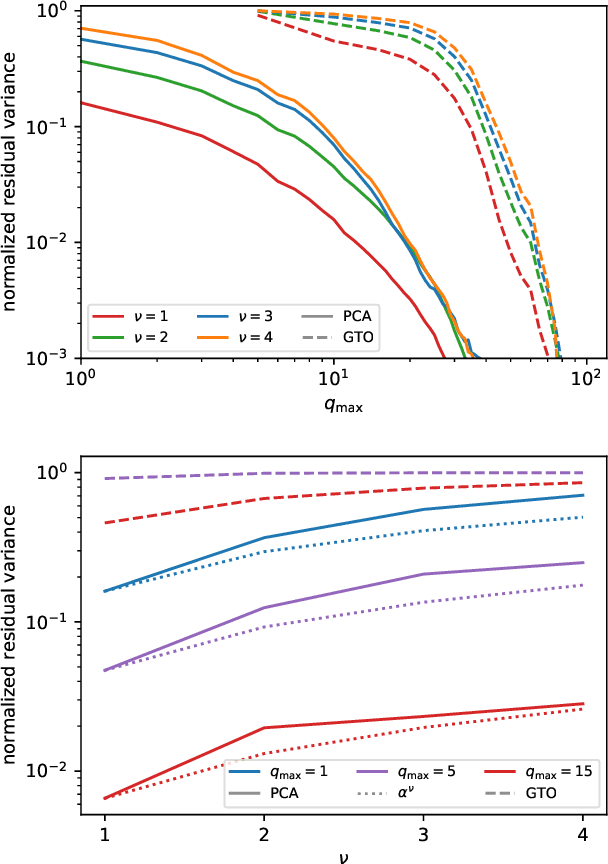
The input of almost every machine learning algorithm targeting the properties of matter at the atomic scale involves a transformation of the list of Cartesian atomic coordinates into a more symmetric representation. Many of these most popular representations can be seen as an expansion of the symmetrized correlations of the atom density, and differ mainly by the choice of basis. Here we discuss how to build an adaptive, optimal numerical basis that is chosen to represent most efficiently the structural diversity of the dataset at hand. For each training dataset, this optimal basis is unique, and can be computed at no additional cost with respect to the primitive basis by approximating it with splines. We demonstrate that this construction yields representations that are accurate and computationally efficient, presenting examples that involve both molecular and condensed-phase machine-learning models.