PET-MAD, a universal interatomic potential for advanced materials modeling

Machine-learning interatomic potentials (MLIPs) have greatly extended the reach of atomic-scale simulations, offering the accuracy of first-principles calculations at a fraction of the effort. Leveraging large quantum mechanical databases and expressive architectures, recent "universal" models deliver qualitative accuracy across the periodic table but are often biased toward low-energy configurations. We introduce PET-MAD, a generally applicable MLIP trained on a dataset combining stable inorganic and organic solids, systematically modified to enhance atomic diversity. Using a moderate but highly-consistent level of electronic-structure theory, we assess PET-MAD's accuracy on established benchmarks and advanced simulations of six materials. PET-MAD rivals state-of-the-art MLIPs for inorganic solids, while also being reliable for molecules, organic materials, and surfaces. It is stable and fast, enabling, out-of-the-box, the near-quantitative study of thermal and quantum mechanical fluctuations, functional properties, and phase transitions. It can be efficiently fine-tuned to deliver full quantum mechanical accuracy with a minimal number of targeted calculations.

Unified theory of atom-centered representations and graph convolutional machine-learning schemes

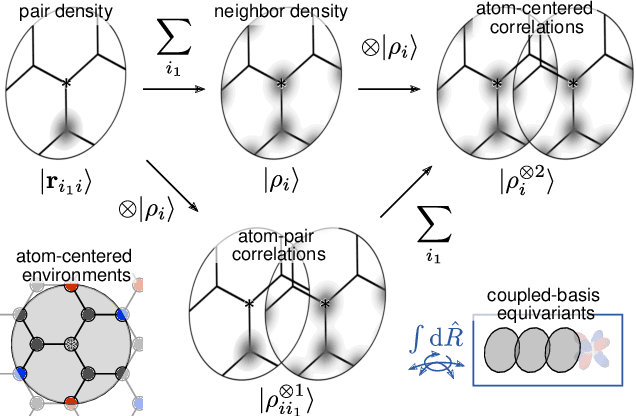
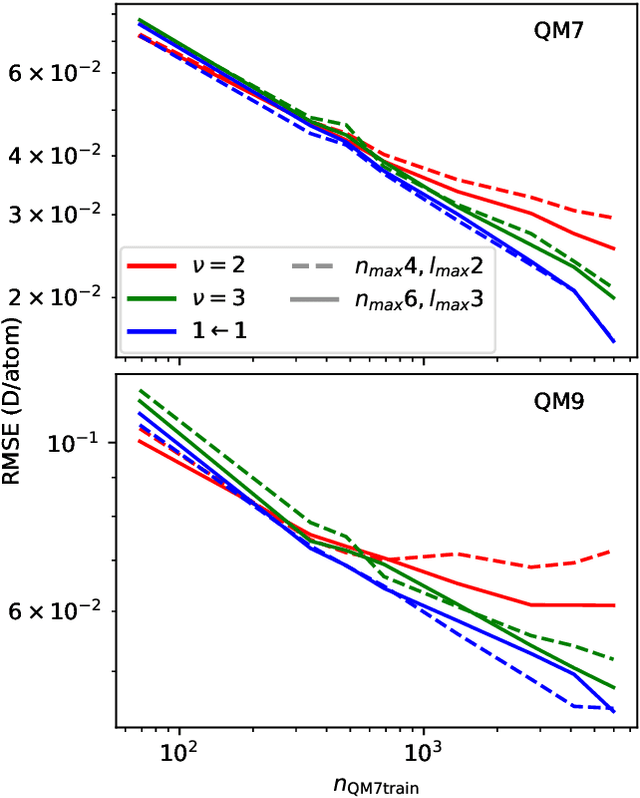
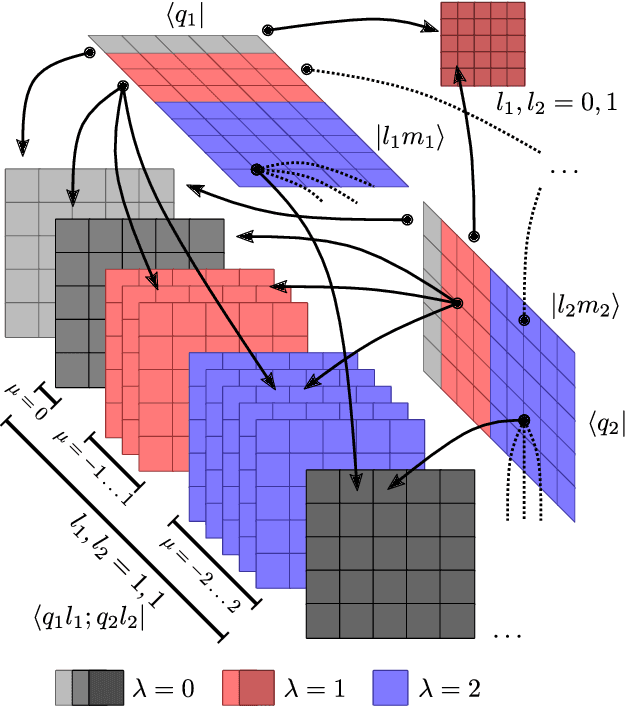
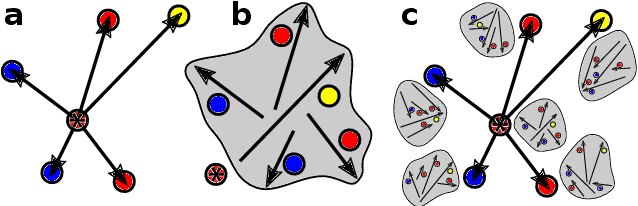
Data-driven schemes that associate molecular and crystal structures with their microscopic properties share the need for a concise, effective description of the arrangement of their atomic constituents. Many types of models rely on descriptions of atom-centered environments, that are associated with an atomic property or with an atomic contribution to an extensive macroscopic quantity. Frameworks in this class can be understood in terms of atom-centered density correlations (ACDC), that are used as a basis for a body-ordered, symmetry-adapted expansion of the targets. Several other schemes, that gather information on the relationship between neighboring atoms using graph-convolutional (or message-passing) ideas, cannot be directly mapped to correlations centered around a single atom. We generalize the ACDC framework to include multi-centered information, generating representations that provide a complete linear basis to regress symmetric functions of atomic coordinates, and form the basis to systematize our understanding of both atom-centered and graph-convolutional machine-learning schemes.

The role of feature space in atomistic learning

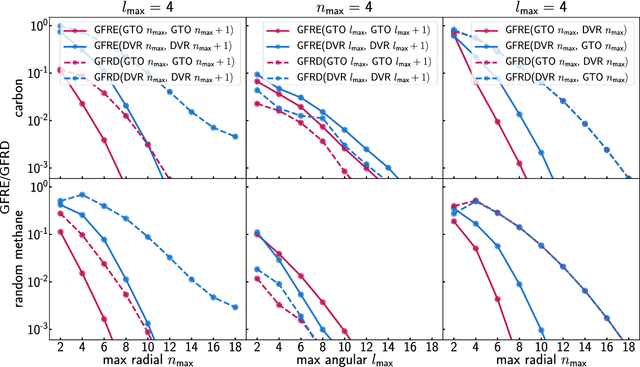
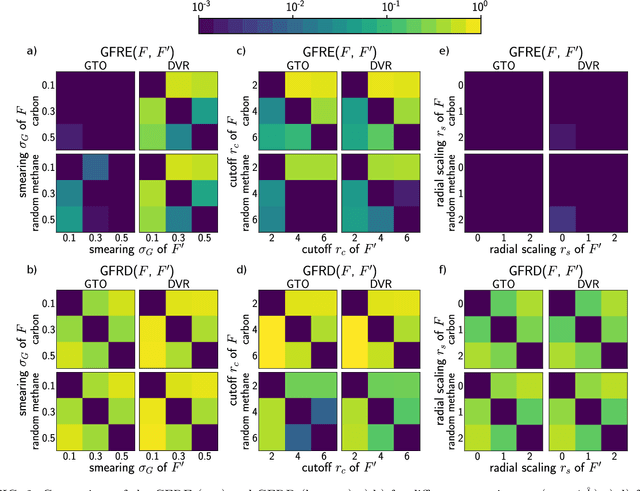
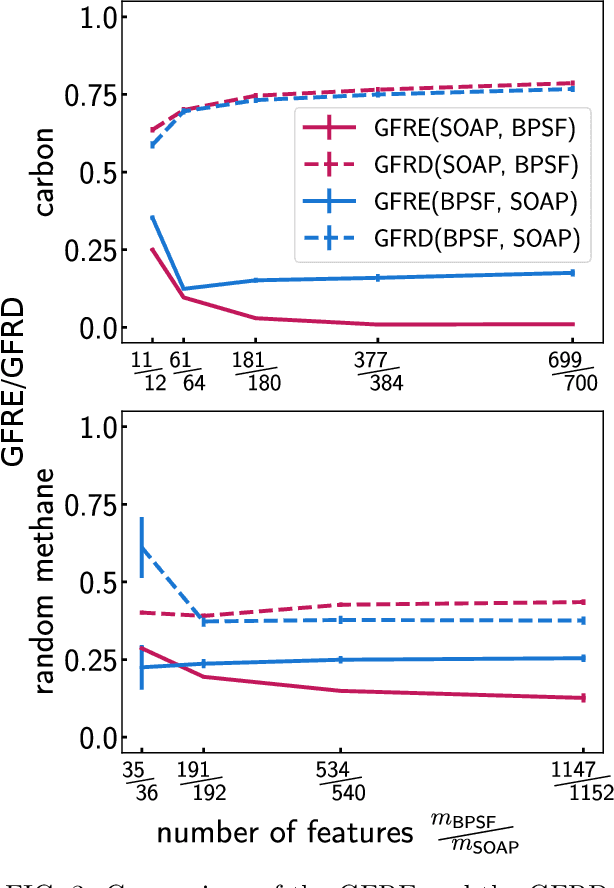
Efficient, physically-inspired descriptors of the structure and composition of molecules and materials play a key role in the application of machine-learning techniques to atomistic simulations. The proliferation of approaches, as well as the fact that each choice of features can lead to very different behavior depending on how they are used, e.g. by introducing non-linear kernels and non-Euclidean metrics to manipulate them, makes it difficult to objectively compare different methods, and to address fundamental questions on how one feature space is related to another. In this work we introduce a framework to compare different sets of descriptors, and different ways of transforming them by means of metrics and kernels, in terms of the structure of the feature space that they induce. We define diagnostic tools to determine whether alternative feature spaces contain equivalent amounts of information, and whether the common information is substantially distorted when going from one feature space to another. We compare, in particular, representations that are built in terms of $n$-body correlations of the atom density, quantitatively assessing the information loss associated with the use of low-order features. We also investigate the impact of different choices of basis functions and hyperparameters of the widely used SOAP and Behler-Parrinello features, and investigate how the use of non-linear kernels, and of a Wasserstein-type metric, change the structure of the feature space in comparison to a simpler linear feature space.

Structure-Property Maps with Kernel Principal Covariates Regression

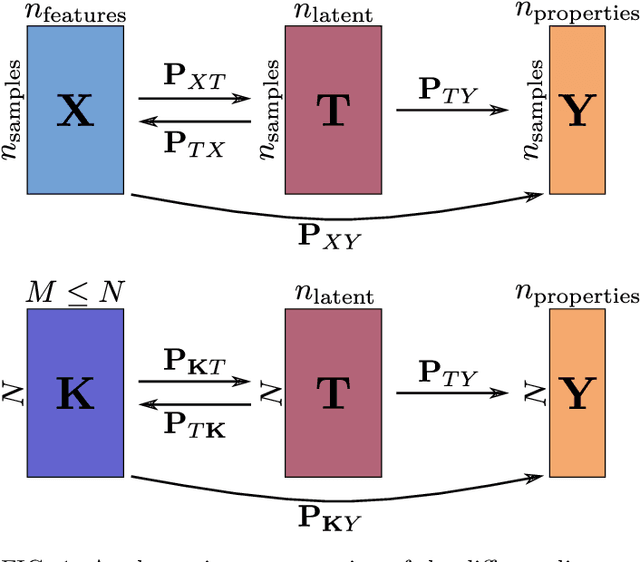
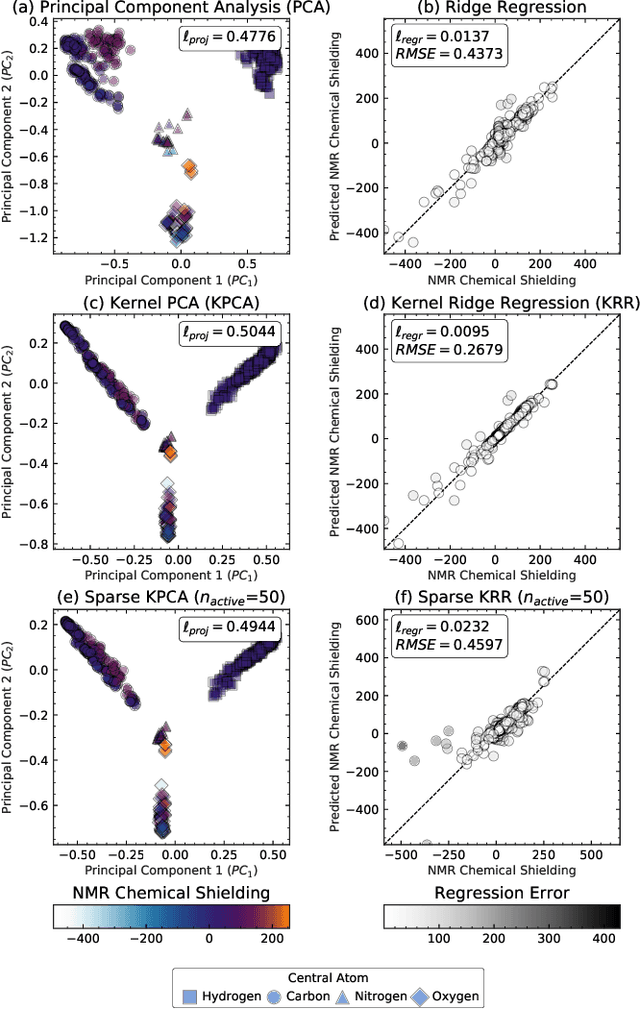
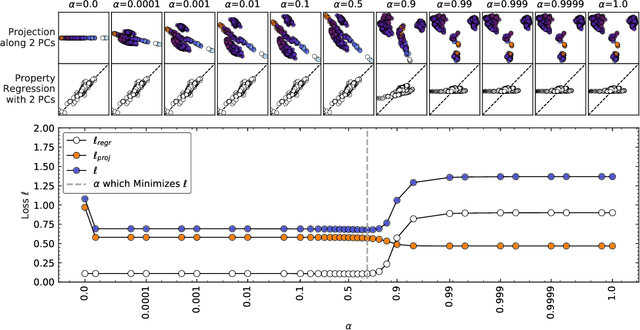
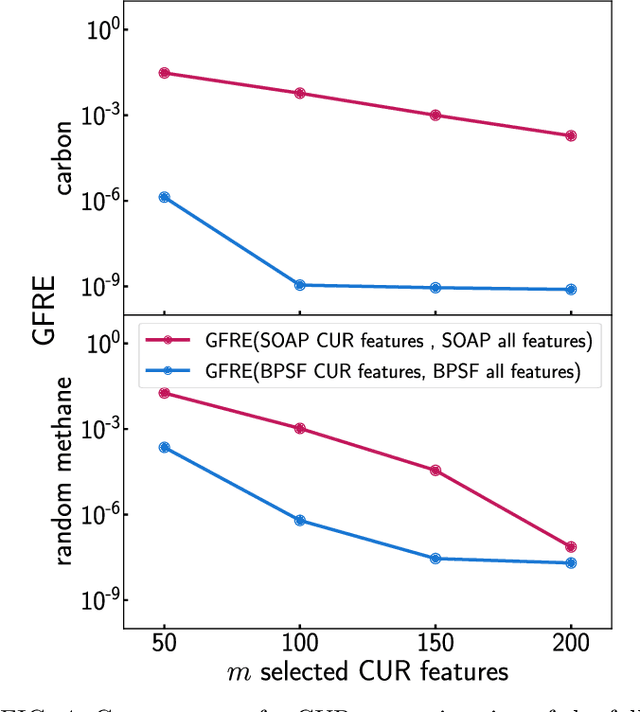
Data analysis based on linear methods, which look for correlations between the features describing samples in a data set, or between features and properties associated with the samples, constitute the simplest, most robust, and transparent approaches to the automatic processing of large amounts of data for building supervised or unsupervised machine learning models. Principal covariates regression (PCovR) is an under-appreciated method that interpolates between principal component analysis and linear regression, and can be used to conveniently reveal structure-property relations in terms of simple-to-interpret, low-dimensional maps. Here we provide a pedagogic overview of these data analysis schemes, including the use of the kernel trick to introduce an element of non-linearity in the process, while maintaining most of the convenience and the simplicity of linear approaches. We then introduce a kernelized version of PCovR and a sparsified extension, followed by a feature-selection scheme based on the CUR matrix decomposition modified to incorporate the same hybrid loss that underlies PCovR. We demonstrate the performance of these approaches in revealing and predicting structure-property relations in chemistry and materials science.