Structure-Property Maps with Kernel Principal Covariates Regression

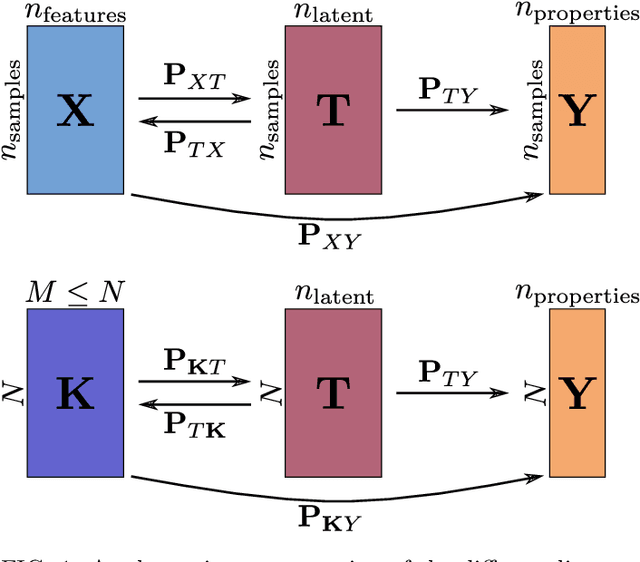
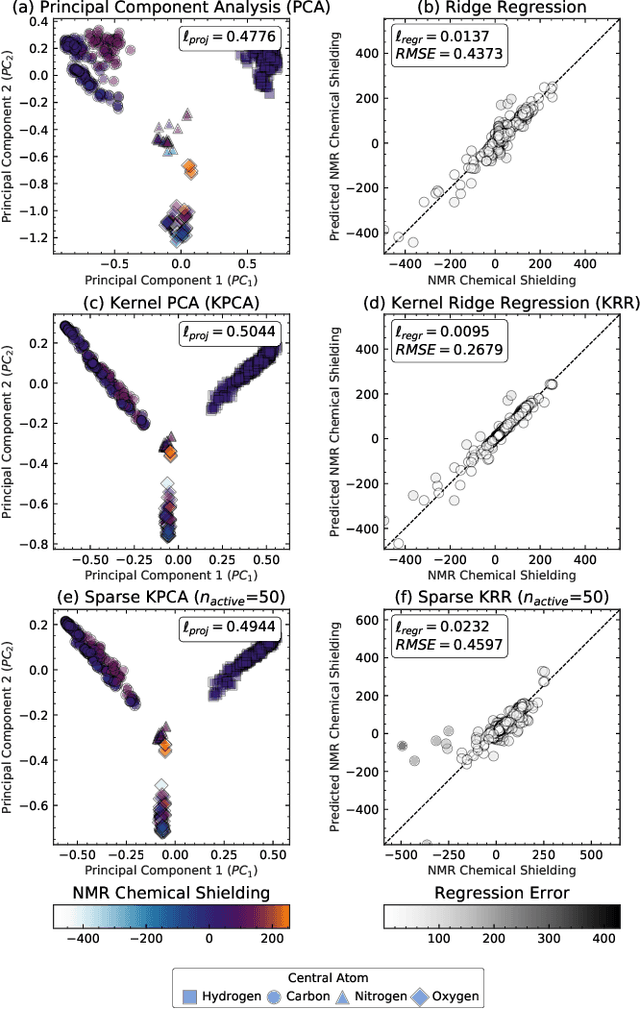
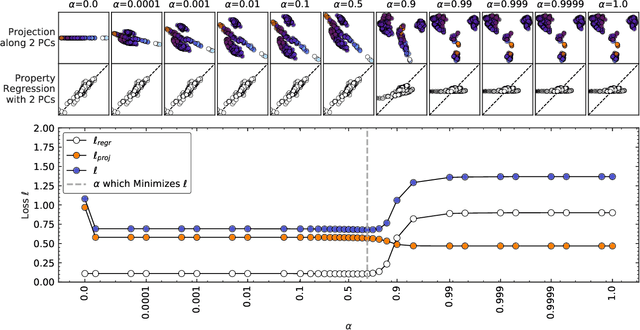
Data analysis based on linear methods, which look for correlations between the features describing samples in a data set, or between features and properties associated with the samples, constitute the simplest, most robust, and transparent approaches to the automatic processing of large amounts of data for building supervised or unsupervised machine learning models. Principal covariates regression (PCovR) is an under-appreciated method that interpolates between principal component analysis and linear regression, and can be used to conveniently reveal structure-property relations in terms of simple-to-interpret, low-dimensional maps. Here we provide a pedagogic overview of these data analysis schemes, including the use of the kernel trick to introduce an element of non-linearity in the process, while maintaining most of the convenience and the simplicity of linear approaches. We then introduce a kernelized version of PCovR and a sparsified extension, followed by a feature-selection scheme based on the CUR matrix decomposition modified to incorporate the same hybrid loss that underlies PCovR. We demonstrate the performance of these approaches in revealing and predicting structure-property relations in chemistry and materials science.