Improving Sample and Feature Selection with Principal Covariates Regression

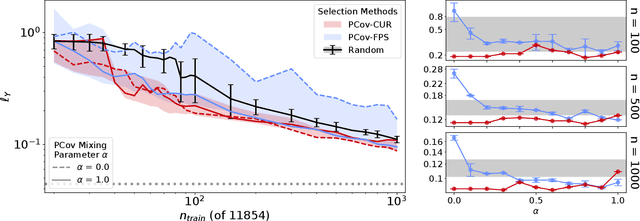
Selecting the most relevant features and samples out of a large set of candidates is a task that occurs very often in the context of automated data analysis, where it can be used to improve the computational performance, and also often the transferability, of a model. Here we focus on two popular sub-selection schemes which have been applied to this end: CUR decomposition, that is based on a low-rank approximation of the feature matrix and Farthest Point Sampling, that relies on the iterative identification of the most diverse samples and discriminating features. We modify these unsupervised approaches, incorporating a supervised component following the same spirit as the Principal Covariates Regression (PCovR) method. We show that incorporating target information provides selections that perform better in supervised tasks, which we demonstrate with ridge regression, kernel ridge regression, and sparse kernel regression. We also show that incorporating aspects of simple supervised learning models can improve the accuracy of more complex models, such as feed-forward neural networks. We present adjustments to minimize the impact that any subselection may incur when performing unsupervised tasks. We demonstrate the significant improvements associated with the use of PCov-CUR and PCov-FPS selections for applications to chemistry and materials science, typically reducing by a factor of two the number of features and samples which are required to achieve a given level of regression accuracy.

Structure-Property Maps with Kernel Principal Covariates Regression

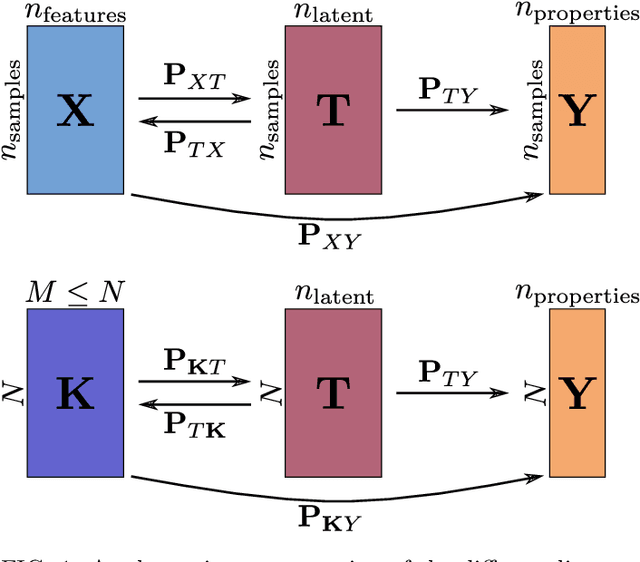
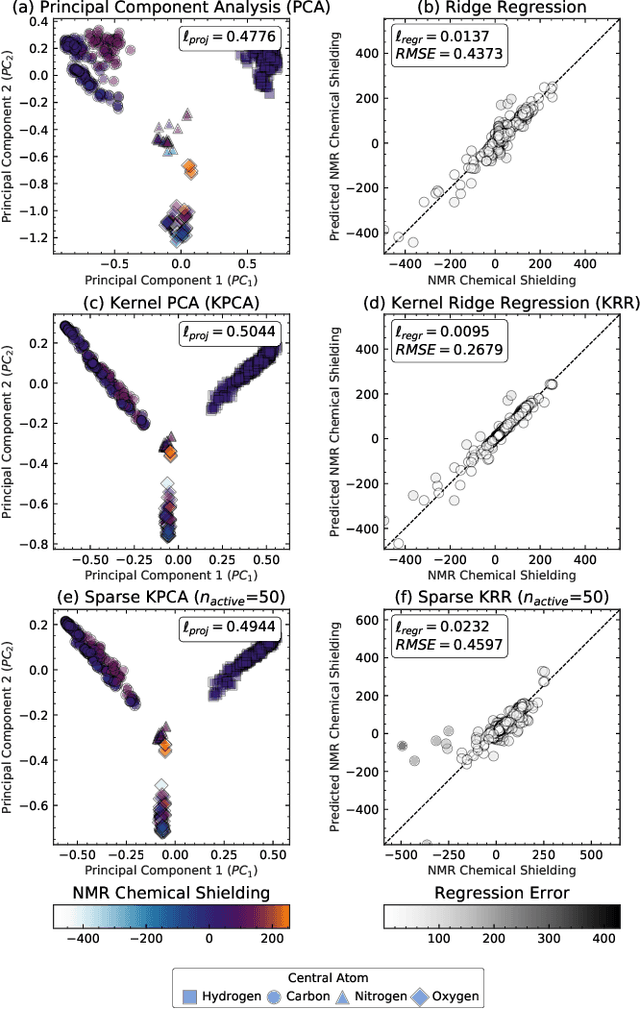
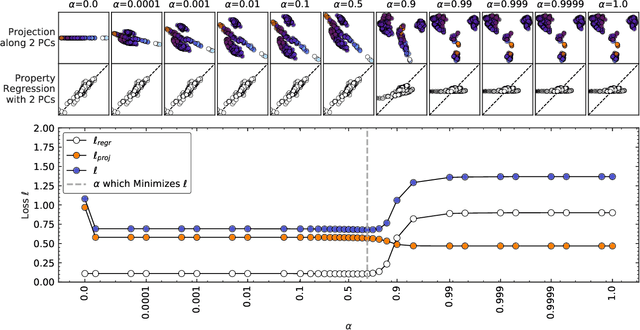
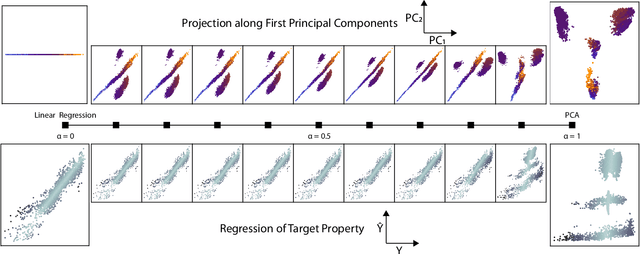
Data analysis based on linear methods, which look for correlations between the features describing samples in a data set, or between features and properties associated with the samples, constitute the simplest, most robust, and transparent approaches to the automatic processing of large amounts of data for building supervised or unsupervised machine learning models. Principal covariates regression (PCovR) is an under-appreciated method that interpolates between principal component analysis and linear regression, and can be used to conveniently reveal structure-property relations in terms of simple-to-interpret, low-dimensional maps. Here we provide a pedagogic overview of these data analysis schemes, including the use of the kernel trick to introduce an element of non-linearity in the process, while maintaining most of the convenience and the simplicity of linear approaches. We then introduce a kernelized version of PCovR and a sparsified extension, followed by a feature-selection scheme based on the CUR matrix decomposition modified to incorporate the same hybrid loss that underlies PCovR. We demonstrate the performance of these approaches in revealing and predicting structure-property relations in chemistry and materials science.