Optimal radial basis for density-based atomic representations

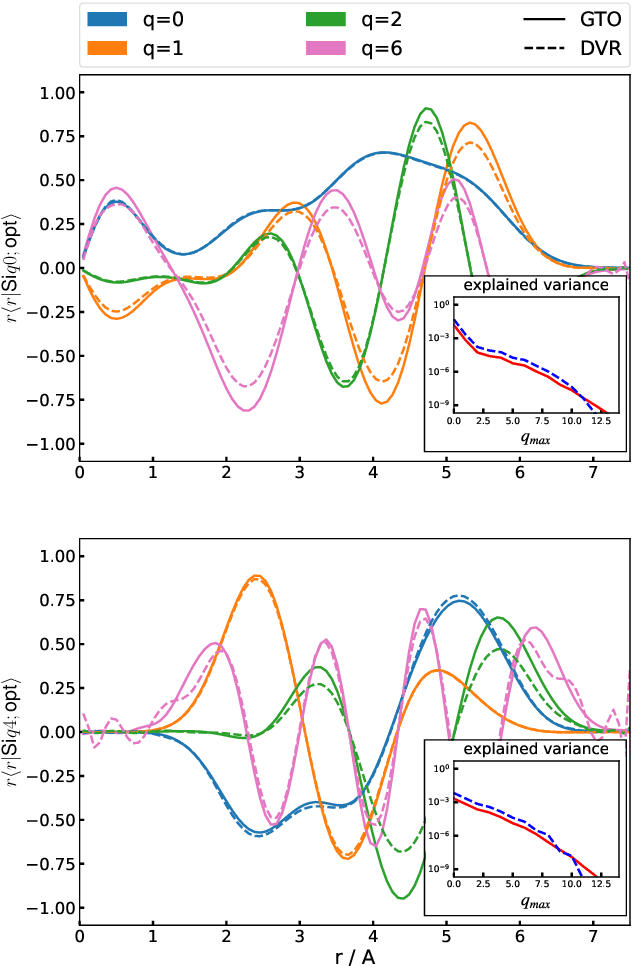
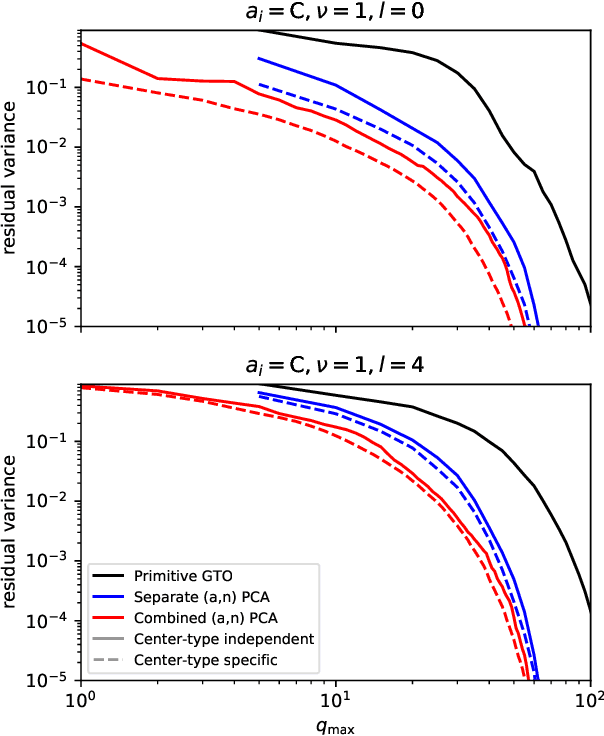
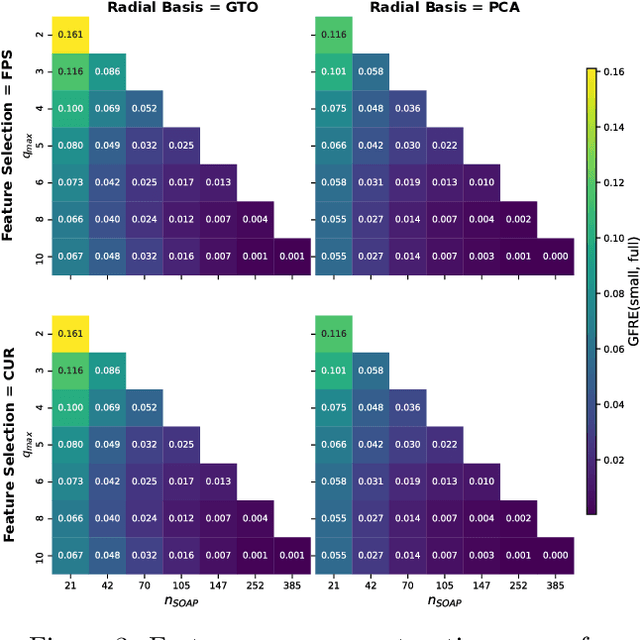
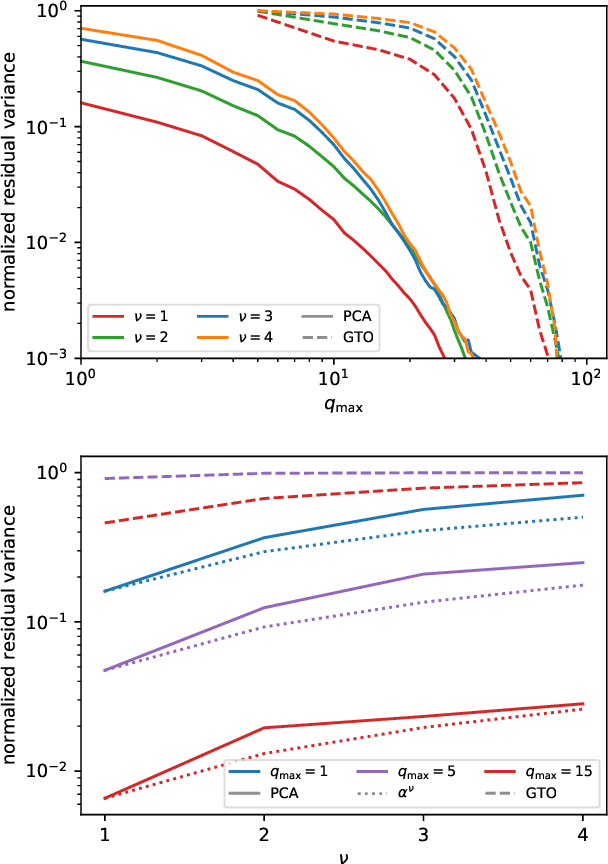
The input of almost every machine learning algorithm targeting the properties of matter at the atomic scale involves a transformation of the list of Cartesian atomic coordinates into a more symmetric representation. Many of these most popular representations can be seen as an expansion of the symmetrized correlations of the atom density, and differ mainly by the choice of basis. Here we discuss how to build an adaptive, optimal numerical basis that is chosen to represent most efficiently the structural diversity of the dataset at hand. For each training dataset, this optimal basis is unique, and can be computed at no additional cost with respect to the primitive basis by approximating it with splines. We demonstrate that this construction yields representations that are accurate and computationally efficient, presenting examples that involve both molecular and condensed-phase machine-learning models.

The role of feature space in atomistic learning

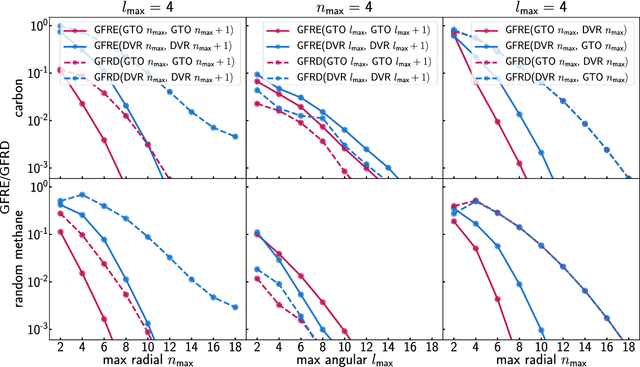
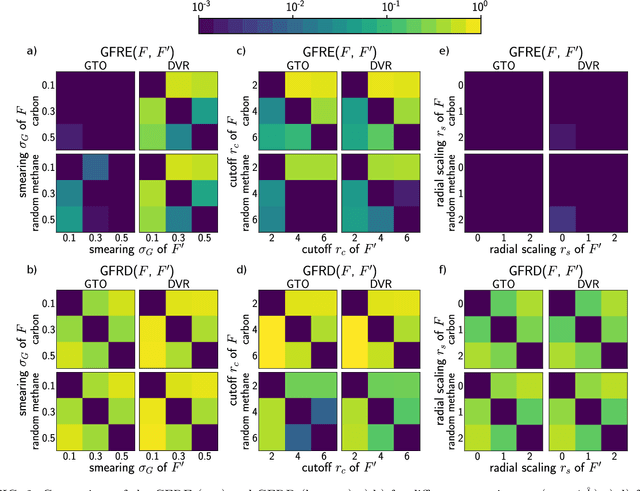
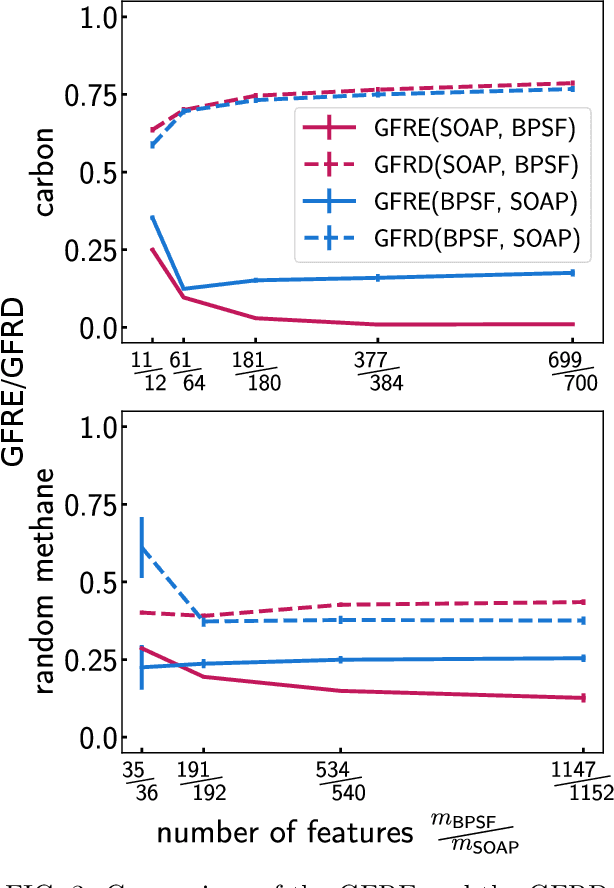
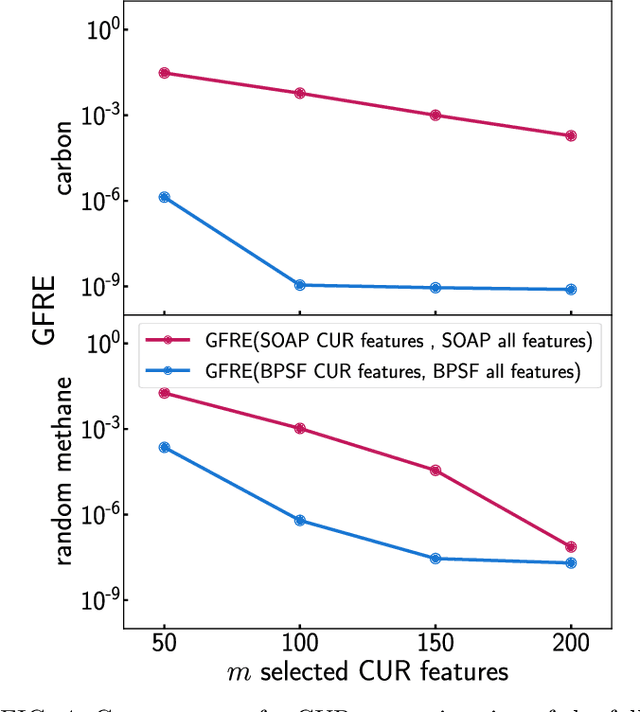
Efficient, physically-inspired descriptors of the structure and composition of molecules and materials play a key role in the application of machine-learning techniques to atomistic simulations. The proliferation of approaches, as well as the fact that each choice of features can lead to very different behavior depending on how they are used, e.g. by introducing non-linear kernels and non-Euclidean metrics to manipulate them, makes it difficult to objectively compare different methods, and to address fundamental questions on how one feature space is related to another. In this work we introduce a framework to compare different sets of descriptors, and different ways of transforming them by means of metrics and kernels, in terms of the structure of the feature space that they induce. We define diagnostic tools to determine whether alternative feature spaces contain equivalent amounts of information, and whether the common information is substantially distorted when going from one feature space to another. We compare, in particular, representations that are built in terms of $n$-body correlations of the atom density, quantitatively assessing the information loss associated with the use of low-order features. We also investigate the impact of different choices of basis functions and hyperparameters of the widely used SOAP and Behler-Parrinello features, and investigate how the use of non-linear kernels, and of a Wasserstein-type metric, change the structure of the feature space in comparison to a simpler linear feature space.