Pushing the limits of unconstrained machine-learned interatomic potentials

Machine-learned interatomic potentials (MLIPs) are increasingly used to replace computationally demanding electronic-structure calculations to model matter at the atomic scale. The most commonly used model architectures are constrained to fulfill a number of physical laws exactly, from geometric symmetries to energy conservation. Evidence is mounting that relaxing some of these constraints can be beneficial to the efficiency and (somewhat surprisingly) accuracy of MLIPs, even though care should be taken to avoid qualitative failures associated with the breaking of physical symmetries. Given the recent trend of \emph{scaling up} models to larger numbers of parameters and training samples, a very important question is how unconstrained MLIPs behave in this limit. Here we investigate this issue, showing that -- when trained on large datasets -- unconstrained models can be superior in accuracy and speed when compared to physically constrained models. We assess these models both in terms of benchmark accuracy and in terms of usability in practical scenarios, focusing on static simulation workflows such as geometry optimization and lattice dynamics. We conclude that accurate unconstrained models can be applied with confidence, especially since simple inference-time modifications can be used to recover observables that are consistent with the relevant physical symmetries.

Representing spherical tensors with scalar-based machine-learning models

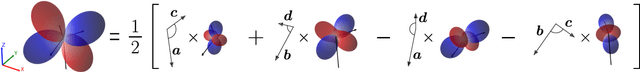
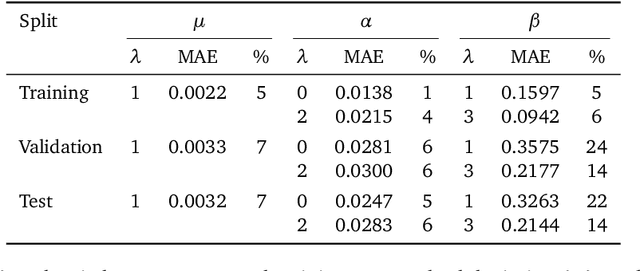
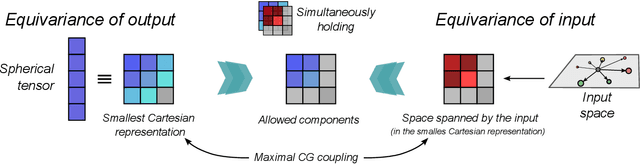
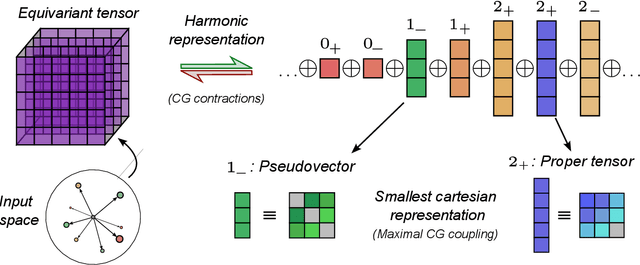
Rotational symmetry plays a central role in physics, providing an elegant framework to describe how the properties of 3D objects -- from atoms to the macroscopic scale -- transform under the action of rigid rotations. Equivariant models of 3D point clouds are able to approximate structure-property relations in a way that is fully consistent with the structure of the rotation group, by combining intermediate representations that are themselves spherical tensors. The symmetry constraints however make this approach computationally demanding and cumbersome to implement, which motivates increasingly popular unconstrained architectures that learn approximate symmetries as part of the training process. In this work, we explore a third route to tackle this learning problem, where equivariant functions are expressed as the product of a scalar function of the point cloud coordinates and a small basis of tensors with the appropriate symmetry. We also propose approximations of the general expressions that, while lacking universal approximation properties, are fast, simple to implement, and accurate in practical settings.

PET-MAD, a universal interatomic potential for advanced materials modeling

Machine-learning interatomic potentials (MLIPs) have greatly extended the reach of atomic-scale simulations, offering the accuracy of first-principles calculations at a fraction of the effort. Leveraging large quantum mechanical databases and expressive architectures, recent "universal" models deliver qualitative accuracy across the periodic table but are often biased toward low-energy configurations. We introduce PET-MAD, a generally applicable MLIP trained on a dataset combining stable inorganic and organic solids, systematically modified to enhance atomic diversity. Using a moderate but highly-consistent level of electronic-structure theory, we assess PET-MAD's accuracy on established benchmarks and advanced simulations of six materials. PET-MAD rivals state-of-the-art MLIPs for inorganic solids, while also being reliable for molecules, organic materials, and surfaces. It is stable and fast, enabling, out-of-the-box, the near-quantitative study of thermal and quantum mechanical fluctuations, functional properties, and phase transitions. It can be efficiently fine-tuned to deliver full quantum mechanical accuracy with a minimal number of targeted calculations.