Electronic excited states from physically-constrained machine learning

Data-driven techniques are increasingly used to replace electronic-structure calculations of matter. In this context, a relevant question is whether machine learning (ML) should be applied directly to predict the desired properties or be combined explicitly with physically-grounded operations. We present an example of an integrated modeling approach, in which a symmetry-adapted ML model of an effective Hamiltonian is trained to reproduce electronic excitations from a quantum-mechanical calculation. The resulting model can make predictions for molecules that are much larger and more complex than those that it is trained on, and allows for dramatic computational savings by indirectly targeting the outputs of well-converged calculations while using a parameterization corresponding to a minimal atom-centered basis. These results emphasize the merits of intertwining data-driven techniques with physical approximations, improving the transferability and interpretability of ML models without affecting their accuracy and computational efficiency, and providing a blueprint for developing ML-augmented electronic-structure methods.

Completeness of Atomic Structure Representations

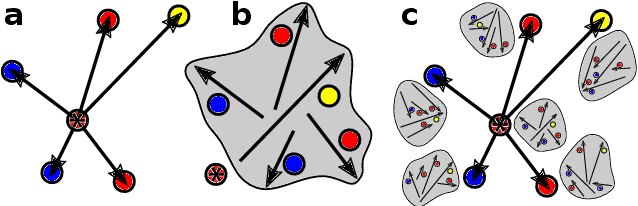
Achieving a complete and symmetric description of a group of point particles, such as atoms in a molecule, is a common problem in physics and theoretical chemistry. The introduction of machine learning to science has made this issue even more critical, as it underpins the ability of a model to reproduce arbitrary physical relationships, and to do so while being consistent with basic symmetries and conservation laws. However, the descriptors that are commonly used to represent point clouds -- most notably those adopted to describe matter at the atomic scale -- are unable to distinguish between special arrangements of particles. This makes it impossible to machine learn their properties. Frameworks that are provably complete exist, but are only so in the limit in which they simultaneously describe the mutual relationship between all atoms, which is impractical. We introduce, and demonstrate on a particularly insidious class of atomic arrangements, a strategy to build descriptors that rely solely on information on the relative arrangement of triplets of particles, but can be used to construct symmetry-adapted models that have universal approximation power.

Unified theory of atom-centered representations and graph convolutional machine-learning schemes

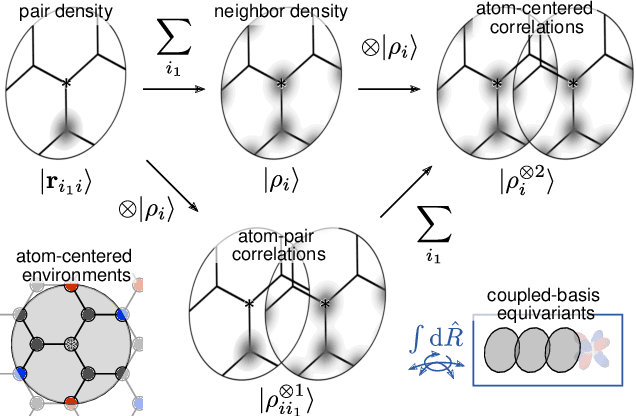
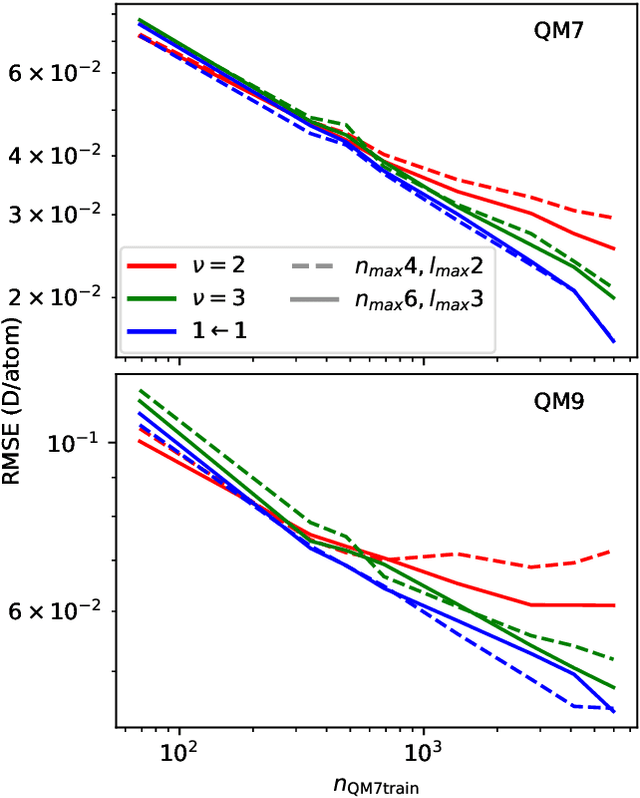
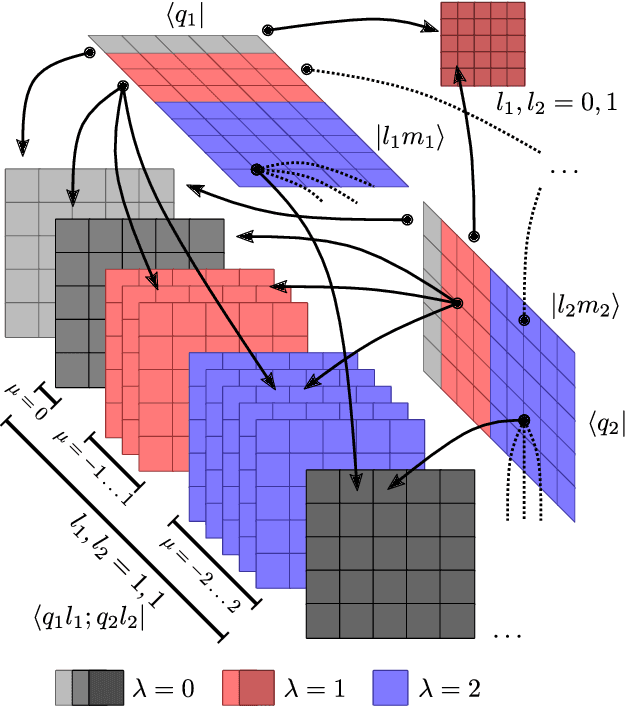
Data-driven schemes that associate molecular and crystal structures with their microscopic properties share the need for a concise, effective description of the arrangement of their atomic constituents. Many types of models rely on descriptions of atom-centered environments, that are associated with an atomic property or with an atomic contribution to an extensive macroscopic quantity. Frameworks in this class can be understood in terms of atom-centered density correlations (ACDC), that are used as a basis for a body-ordered, symmetry-adapted expansion of the targets. Several other schemes, that gather information on the relationship between neighboring atoms using graph-convolutional (or message-passing) ideas, cannot be directly mapped to correlations centered around a single atom. We generalize the ACDC framework to include multi-centered information, generating representations that provide a complete linear basis to regress symmetric functions of atomic coordinates, and form the basis to systematize our understanding of both atom-centered and graph-convolutional machine-learning schemes.

Equivariant representations for molecular Hamiltonians and N-center atomic-scale properties

Symmetry considerations are at the core of the major frameworks used to provide an effective mathematical representation of atomic configurations, that are then used in machine-learning models to predict the properties associated with each structure. In most cases, the models rely on a description of atom-centered environments, and are suitable to learn atomic properties, or global observables that can be decomposed into atomic contributions. Many quantities that are relevant for quantum mechanical calculations, however -- most notably the Hamiltonian matrix when written in an atomic-orbital basis -- are not associated with a single center, but with two (or more) atoms in the structure. We discuss a family of structural descriptors that generalize the very successful atom-centered density correlation features to the N-centers case, and show in particular how this construction can be applied to efficiently learn the matrix elements of the (effective) single-particle Hamiltonian written in an atom-centered orbital basis. These N-centers features are fully equivariant -- not only in terms of translations and rotations, but also in terms of permutations of the indices associated with the atoms -- and lay the foundations for symmetry-adapted machine-learning models of new classes of properties of molecules and materials.

Multi-scale approach for the prediction of atomic scale properties

Electronic nearsightedness is one of the fundamental principles governing the behavior of condensed matter and supporting its description in terms of local entities such as chemical bonds. Locality also underlies the tremendous success of machine-learning schemes that predict quantum mechanical observables -- such as the cohesive energy, the electron density, or a variety of response properties -- as a sum of atom-centred contributions, based on a short-range representation of atomic environments. One of the main shortcomings of these approaches is their inability to capture physical effects, ranging from electrostatic interactions to quantum delocalization, which have a long-range nature. Here we show how to build a multi-scale scheme that combines in the same framework local and non-local information, overcoming such limitations. We show that the simplest version of such features can be put in formal correspondence with a multipole expansion of permanent electrostatics. The data-driven nature of the model construction, however, makes this simple form suitable to tackle also different types of delocalized and collective effects. We present several examples that range from molecular physics, to surface science and biophysics, demonstrating the ability of this multi-scale approach to model interactions driven by electrostatics, polarization and dispersion, as well as the cooperative behavior of dielectric response functions.