Electronic-structure properties from atom-centered predictions of the electron density

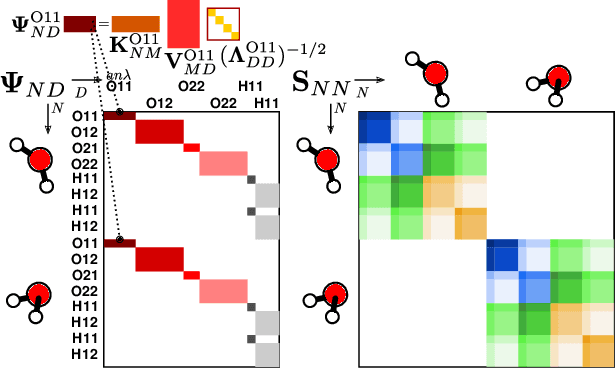
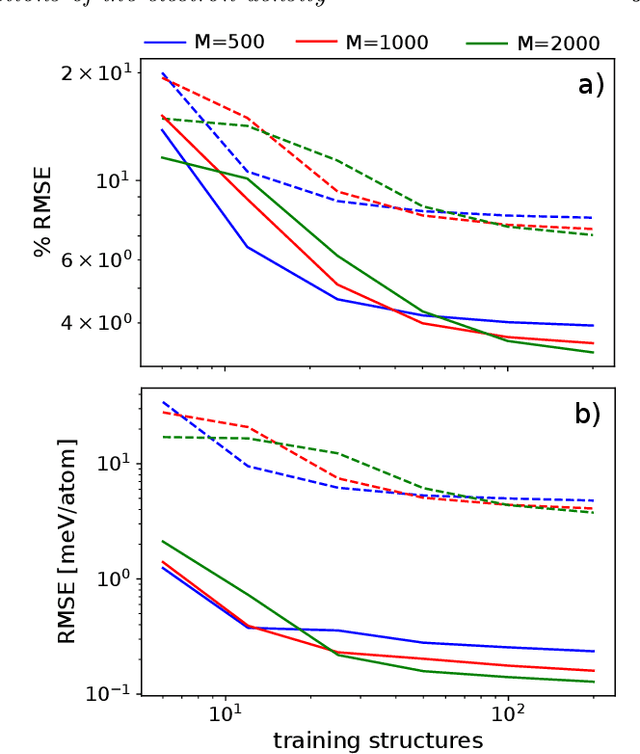
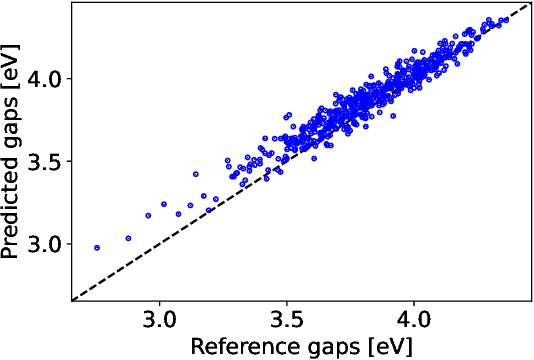
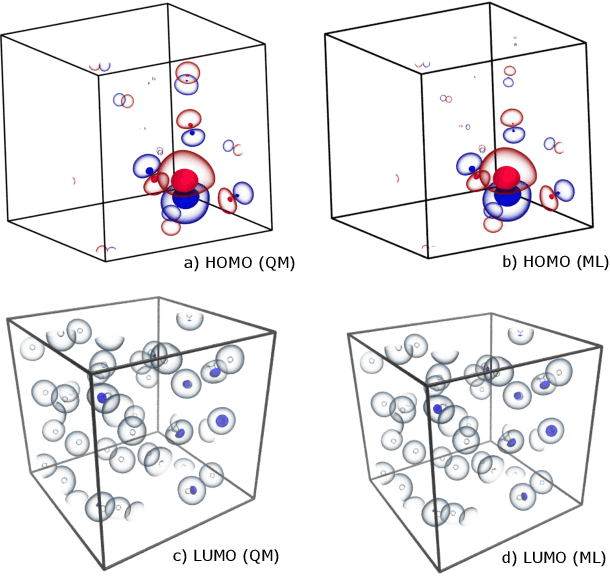
The electron density of a molecule or material has recently received major attention as a target quantity of machine-learning models. A natural choice to construct a model that yields transferable and linear-scaling predictions is to represent the scalar field using a multi-centered atomic basis analogous to that routinely used in density fitting approximations. However, the non-orthogonality of the basis poses challenges for the learning exercise, as it requires accounting for all the atomic density components at once. We devise a gradient-based approach to directly minimize the loss function of the regression problem in an optimized and highly sparse feature space. In so doing, we overcome the limitations associated with adopting an atom-centered model to learn the electron density over arbitrarily complex datasets, obtaining extremely accurate predictions. The enhanced framework is tested on 32-molecule periodic cells of liquid water, presenting enough complexity to require an optimal balance between accuracy and computational efficiency. We show that starting from the predicted density a single Kohn-Sham diagonalization step can be performed to access total energy components that carry an error of just 0.1 meV/atom with respect to the reference density functional calculations. Finally, we test our method on the highly heterogeneous QM9 benchmark dataset, showing that a small fraction of the training data is enough to derive ground-state total energies within chemical accuracy.

Multi-scale approach for the prediction of atomic scale properties

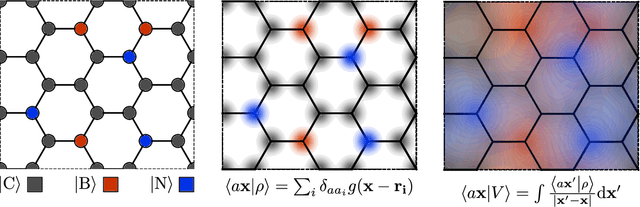
Electronic nearsightedness is one of the fundamental principles governing the behavior of condensed matter and supporting its description in terms of local entities such as chemical bonds. Locality also underlies the tremendous success of machine-learning schemes that predict quantum mechanical observables -- such as the cohesive energy, the electron density, or a variety of response properties -- as a sum of atom-centred contributions, based on a short-range representation of atomic environments. One of the main shortcomings of these approaches is their inability to capture physical effects, ranging from electrostatic interactions to quantum delocalization, which have a long-range nature. Here we show how to build a multi-scale scheme that combines in the same framework local and non-local information, overcoming such limitations. We show that the simplest version of such features can be put in formal correspondence with a multipole expansion of permanent electrostatics. The data-driven nature of the model construction, however, makes this simple form suitable to tackle also different types of delocalized and collective effects. We present several examples that range from molecular physics, to surface science and biophysics, demonstrating the ability of this multi-scale approach to model interactions driven by electrostatics, polarization and dispersion, as well as the cooperative behavior of dielectric response functions.