How big is Big Data?

Big data has ushered in a new wave of predictive power using machine learning models. In this work, we assess what {\it big} means in the context of typical materials-science machine-learning problems. This concerns not only data volume, but also data quality and veracity as much as infrastructure issues. With selected examples, we ask (i) how models generalize to similar datasets, (ii) how high-quality datasets can be gathered from heterogenous sources, (iii) how the feature set and complexity of a model can affect expressivity, and (iv) what infrastructure requirements are needed to create larger datasets and train models on them. In sum, we find that big data present unique challenges along very different aspects that should serve to motivate further work.

Uncertainty Quantification in Deep Neural Networks through Statistical Inference on Latent Space

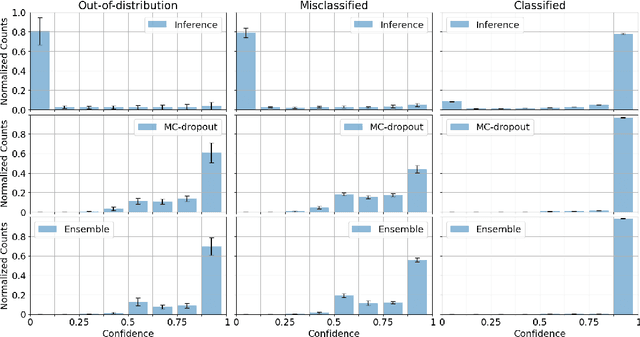
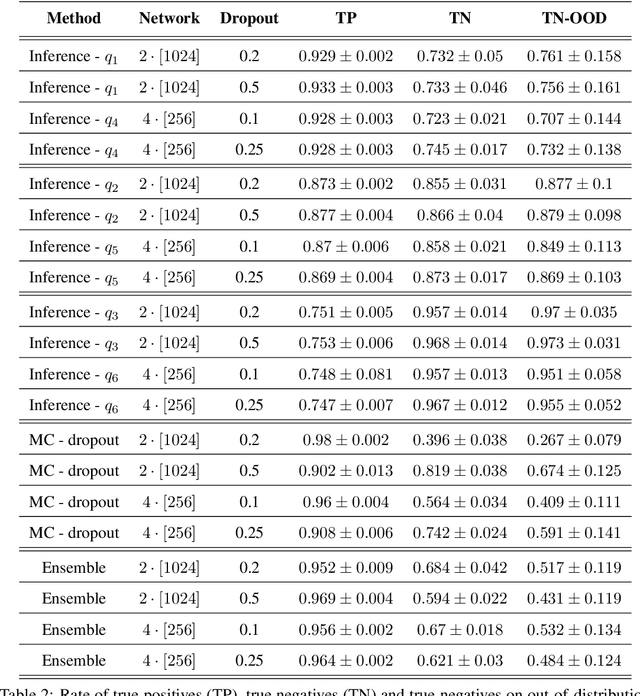
Uncertainty-quantification methods are applied to estimate the confidence of deep-neural-networks classifiers over their predictions. However, most widely used methods are known to be overconfident. We address this problem by developing an algorithm that exploits the latent-space representation of data points fed into the network, to assess the accuracy of their prediction. Using the latent-space representation generated by the fraction of training set that the network classifies correctly, we build a statistical model that is able to capture the likelihood of a given prediction. We show on a synthetic dataset that commonly used methods are mostly overconfident. Overconfidence occurs also for predictions made on data points that are outside the distribution that generated the training data. In contrast, our method can detect such out-of-distribution data points as inaccurately predicted, thus aiding in the automatic detection of outliers.

TCMI: a non-parametric mutual-dependence estimator for multivariate continuous distributions

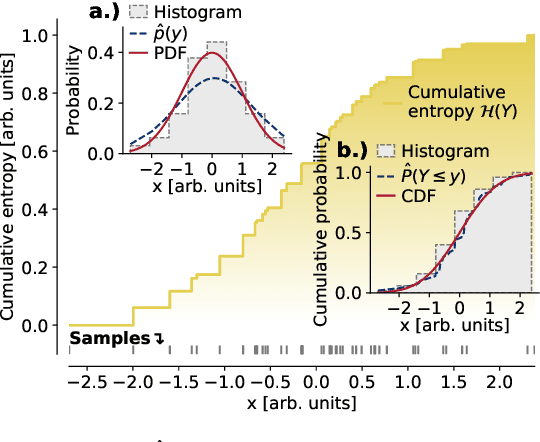
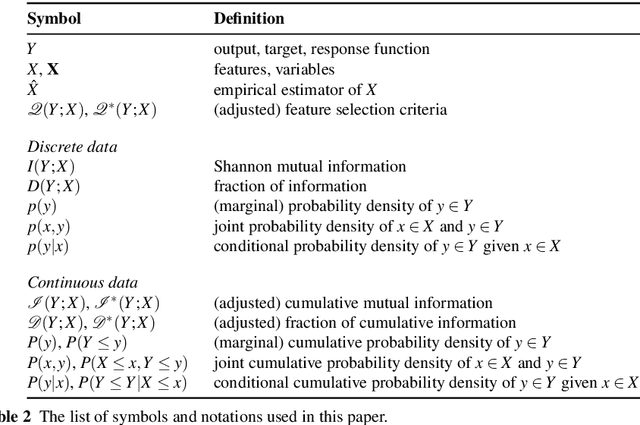
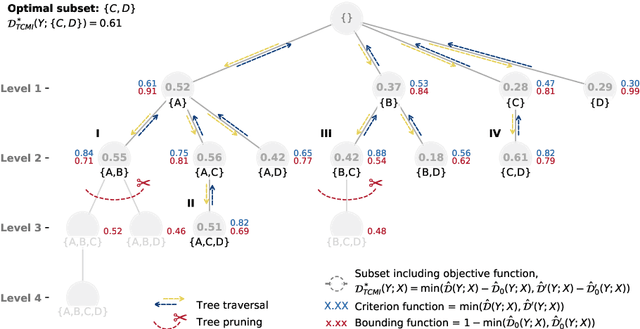
The identification of relevant features, i.e., the driving variables that determine a process or the property of a system, is an essential part of the analysis of data sets whose entries are described by a large number of variables. The preferred measure for quantifying the relevance of nonlinear statistical dependencies is mutual information, which requires as input probability distributions. Probability distributions cannot be reliably sampled and estimated from limited data, especially for real-valued data samples such as lengths or energies. Here, we introduce total cumulative mutual information (TCMI), a measure of the relevance of mutual dependencies based on cumulative probability distributions. TCMI can be estimated directly from sample data and is a non-parametric, robust and deterministic measure that facilitates comparisons and rankings between feature sets with different cardinality. The ranking induced by TCMI allows for feature selection, i.e., the identification of the set of relevant features that are statistical related to the process or the property of a system, while taking into account the number of data samples as well as the cardinality of the feature subsets. We evaluate the performance of our measure with simulated data, compare its performance with similar multivariate dependence measures, and demonstrate the effectiveness of our feature selection method on a set of standard data sets and a typical scenario in materials science.

Identifying Consistent Statements about Numerical Data with Dispersion-Corrected Subgroup Discovery

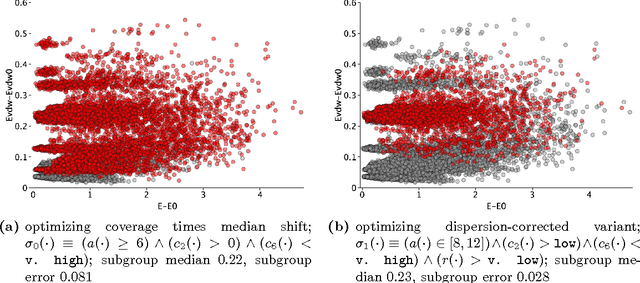
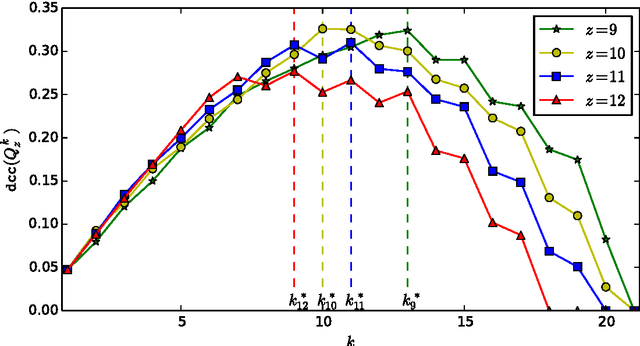
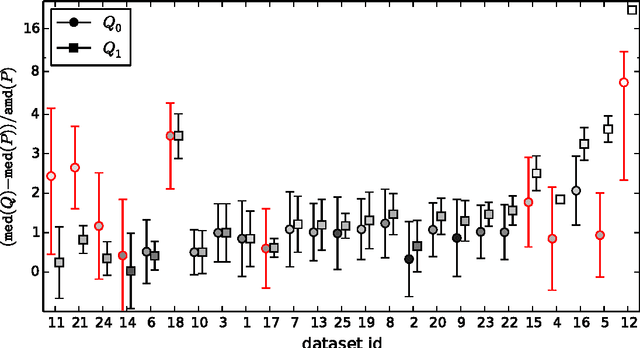
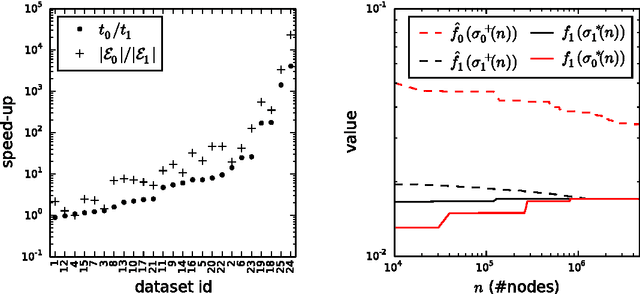
Existing algorithms for subgroup discovery with numerical targets do not optimize the error or target variable dispersion of the groups they find. This often leads to unreliable or inconsistent statements about the data, rendering practical applications, especially in scientific domains, futile. Therefore, we here extend the optimistic estimator framework for optimal subgroup discovery to a new class of objective functions: we show how tight estimators can be computed efficiently for all functions that are determined by subgroup size (non-decreasing dependence), the subgroup median value, and a dispersion measure around the median (non-increasing dependence). In the important special case when dispersion is measured using the average absolute deviation from the median, this novel approach yields a linear time algorithm. Empirical evaluation on a wide range of datasets shows that, when used within branch-and-bound search, this approach is highly efficient and indeed discovers subgroups with much smaller errors.