Emergence of Latent Binary Encoding in Deep Neural Network Classifiers

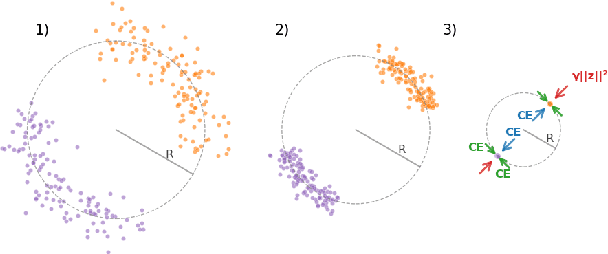
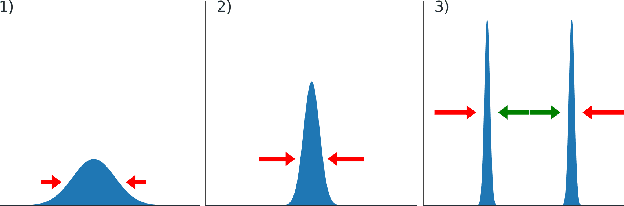
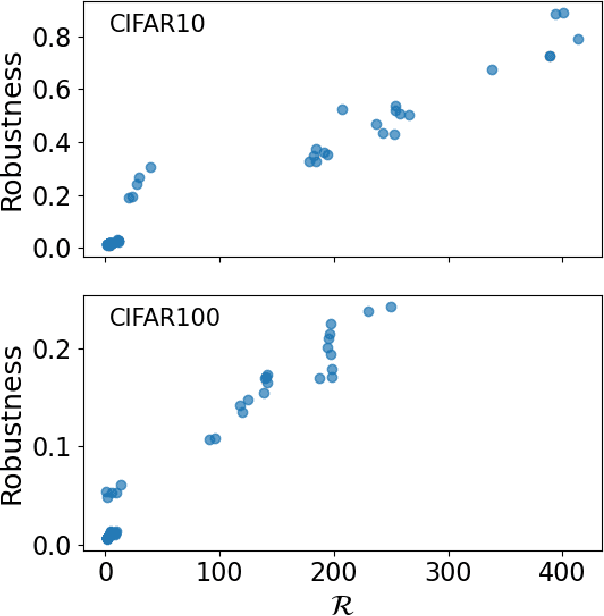
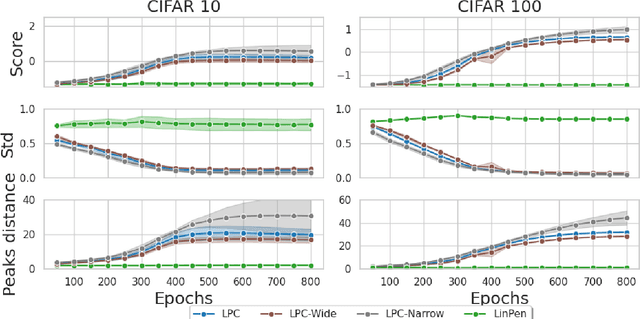
We observe the emergence of binary encoding within the latent space of deep-neural-network classifiers. Such binary encoding is induced by introducing a linear penultimate layer, which is equipped during training with a loss function that grows as $\exp(\vec{x}^2)$, where $\vec{x}$ are the coordinates in the latent space. The phenomenon we describe represents a specific instance of a well-documented occurrence known as \textit{neural collapse}, which arises in the terminal phase of training and entails the collapse of latent class means to the vertices of a simplex equiangular tight frame (ETF). We show that binary encoding accelerates convergence toward the simplex ETF and enhances classification accuracy.

Uncertainty Quantification in Deep Neural Networks through Statistical Inference on Latent Space

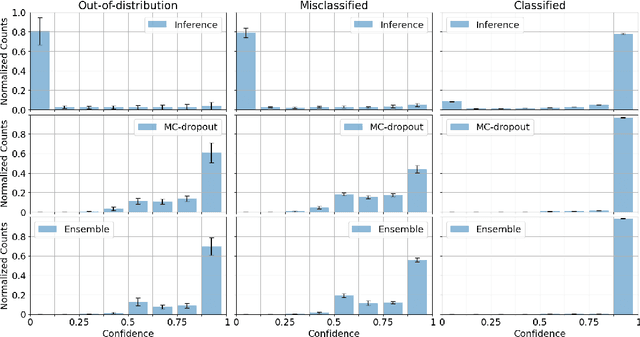
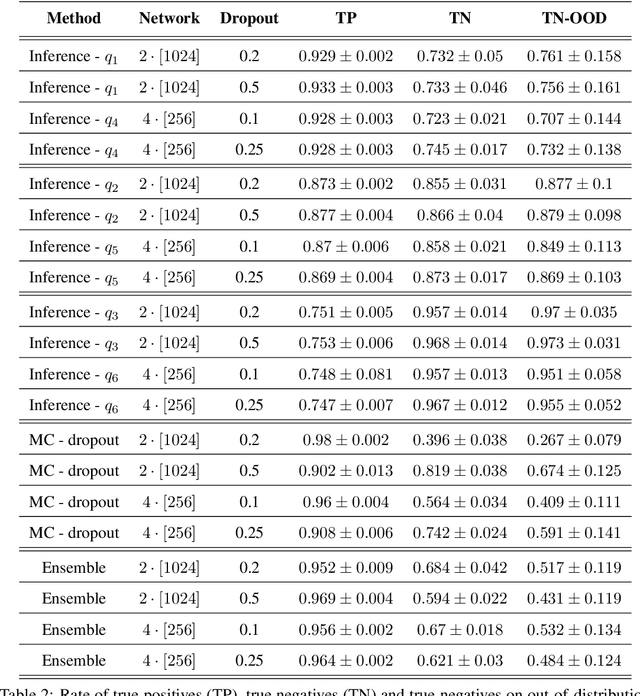
Uncertainty-quantification methods are applied to estimate the confidence of deep-neural-networks classifiers over their predictions. However, most widely used methods are known to be overconfident. We address this problem by developing an algorithm that exploits the latent-space representation of data points fed into the network, to assess the accuracy of their prediction. Using the latent-space representation generated by the fraction of training set that the network classifies correctly, we build a statistical model that is able to capture the likelihood of a given prediction. We show on a synthetic dataset that commonly used methods are mostly overconfident. Overconfidence occurs also for predictions made on data points that are outside the distribution that generated the training data. In contrast, our method can detect such out-of-distribution data points as inaccurately predicted, thus aiding in the automatic detection of outliers.