Emergence of Latent Binary Encoding in Deep Neural Network Classifiers
Paper and Code
Oct 12, 2023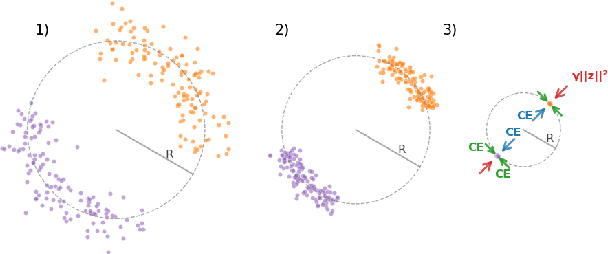
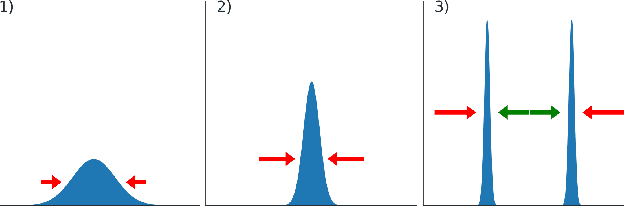
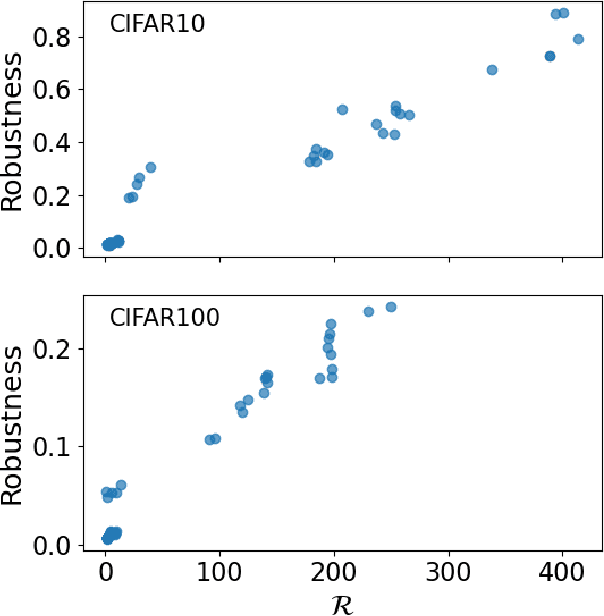
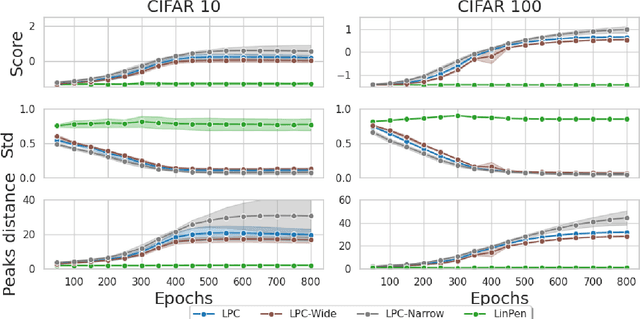
We observe the emergence of binary encoding within the latent space of deep-neural-network classifiers. Such binary encoding is induced by introducing a linear penultimate layer, which is equipped during training with a loss function that grows as $\exp(\vec{x}^2)$, where $\vec{x}$ are the coordinates in the latent space. The phenomenon we describe represents a specific instance of a well-documented occurrence known as \textit{neural collapse}, which arises in the terminal phase of training and entails the collapse of latent class means to the vertices of a simplex equiangular tight frame (ETF). We show that binary encoding accelerates convergence toward the simplex ETF and enhances classification accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge