Ravichandra Addanki
Large-scale graph representation learning with very deep GNNs and self-supervision
Jul 20, 2021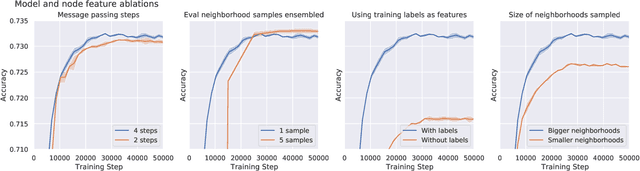
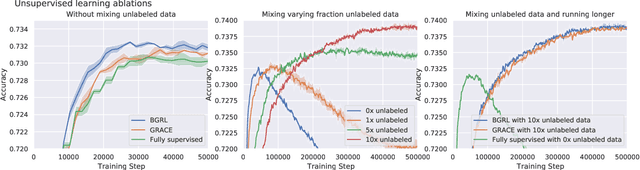
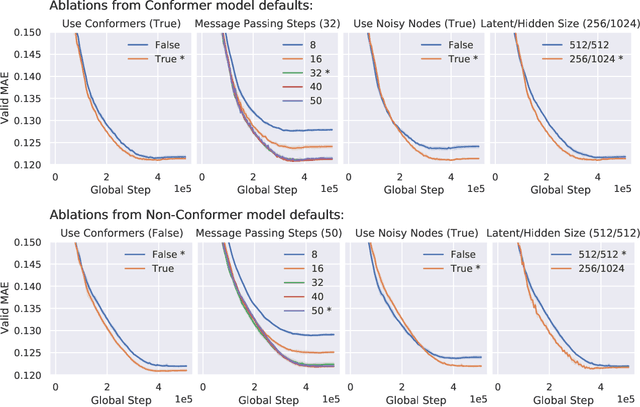
Abstract:Effectively and efficiently deploying graph neural networks (GNNs) at scale remains one of the most challenging aspects of graph representation learning. Many powerful solutions have only ever been validated on comparatively small datasets, often with counter-intuitive outcomes -- a barrier which has been broken by the Open Graph Benchmark Large-Scale Challenge (OGB-LSC). We entered the OGB-LSC with two large-scale GNNs: a deep transductive node classifier powered by bootstrapping, and a very deep (up to 50-layer) inductive graph regressor regularised by denoising objectives. Our models achieved an award-level (top-3) performance on both the MAG240M and PCQM4M benchmarks. In doing so, we demonstrate evidence of scalable self-supervised graph representation learning, and utility of very deep GNNs -- both very important open issues. Our code is publicly available at: https://github.com/deepmind/deepmind-research/tree/master/ogb_lsc.
Solving Mixed Integer Programs Using Neural Networks
Dec 23, 2020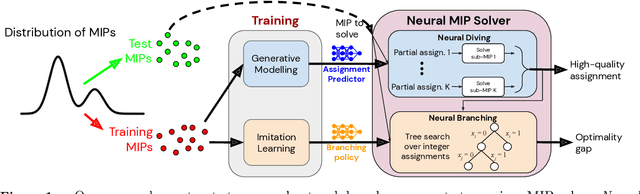
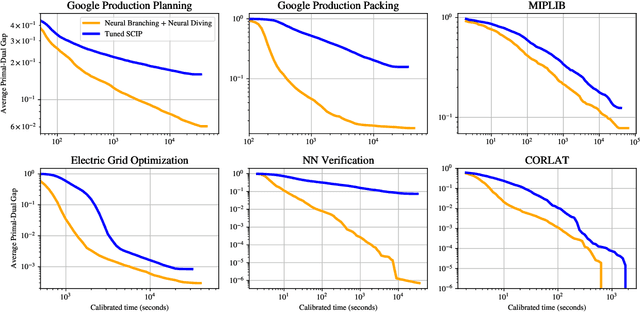
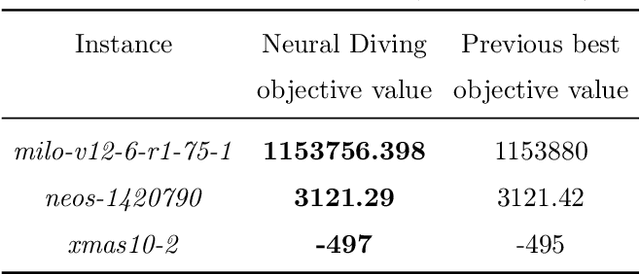
Abstract:Mixed Integer Programming (MIP) solvers rely on an array of sophisticated heuristics developed with decades of research to solve large-scale MIP instances encountered in practice. Machine learning offers to automatically construct better heuristics from data by exploiting shared structure among instances in the data. This paper applies learning to the two key sub-tasks of a MIP solver, generating a high-quality joint variable assignment, and bounding the gap in objective value between that assignment and an optimal one. Our approach constructs two corresponding neural network-based components, Neural Diving and Neural Branching, to use in a base MIP solver such as SCIP. Neural Diving learns a deep neural network to generate multiple partial assignments for its integer variables, and the resulting smaller MIPs for un-assigned variables are solved with SCIP to construct high quality joint assignments. Neural Branching learns a deep neural network to make variable selection decisions in branch-and-bound to bound the objective value gap with a small tree. This is done by imitating a new variant of Full Strong Branching we propose that scales to large instances using GPUs. We evaluate our approach on six diverse real-world datasets, including two Google production datasets and MIPLIB, by training separate neural networks on each. Most instances in all the datasets combined have $10^3-10^6$ variables and constraints after presolve, which is significantly larger than previous learning approaches. Comparing solvers with respect to primal-dual gap averaged over a held-out set of instances, the learning-augmented SCIP is 2x to 10x better on all datasets except one on which it is $10^5$x better, at large time limits. To the best of our knowledge, ours is the first learning approach to demonstrate such large improvements over SCIP on both large-scale real-world application datasets and MIPLIB.
Placeto: Learning Generalizable Device Placement Algorithms for Distributed Machine Learning
Jun 20, 2019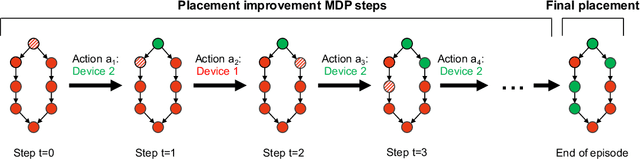
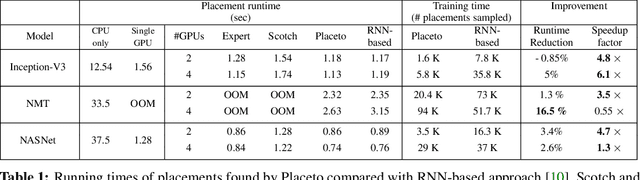
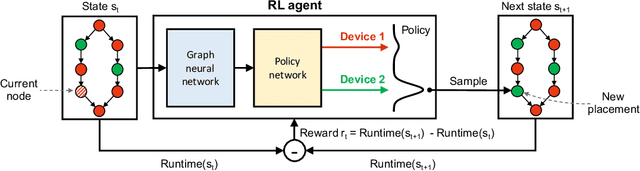
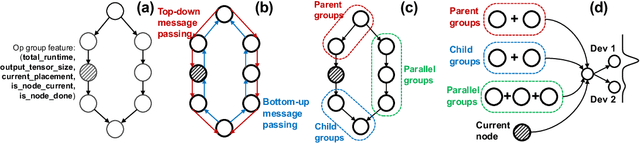
Abstract:We present Placeto, a reinforcement learning (RL) approach to efficiently find device placements for distributed neural network training. Unlike prior approaches that only find a device placement for a specific computation graph, Placeto can learn generalizable device placement policies that can be applied to any graph. We propose two key ideas in our approach: (1) we represent the policy as performing iterative placement improvements, rather than outputting a placement in one shot; (2) we use graph embeddings to capture relevant information about the structure of the computation graph, without relying on node labels for indexing. These ideas allow Placeto to train efficiently and generalize to unseen graphs. Our experiments show that Placeto requires up to 6.1x fewer training steps to find placements that are on par with or better than the best placements found by prior approaches. Moreover, Placeto is able to learn a generalizable placement policy for any given family of graphs, which can then be used without any retraining to predict optimized placements for unseen graphs from the same family. This eliminates the large overhead incurred by prior RL approaches whose lack of generalizability necessitates re-training from scratch every time a new graph is to be placed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge