Natural Quantum Monte Carlo Computation of Excited States

We present a variational Monte Carlo algorithm for estimating the lowest excited states of a quantum system which is a natural generalization of the estimation of ground states. The method has no free parameters and requires no explicit orthogonalization of the different states, instead transforming the problem of finding excited states of a given system into that of finding the ground state of an expanded system. Expected values of arbitrary observables can be calculated, including off-diagonal expectations between different states such as the transition dipole moment. Although the method is entirely general, it works particularly well in conjunction with recent work on using neural networks as variational Ansatze for many-electron systems, and we show that by combining this method with the FermiNet and Psiformer Ansatze we can accurately recover vertical excitation energies and oscillator strengths on molecules as large as benzene. Beyond the examples on molecules presented here, we expect this technique will be of great interest for applications of variational quantum Monte Carlo to atomic, nuclear and condensed matter physics.

Learned Force Fields Are Ready For Ground State Catalyst Discovery

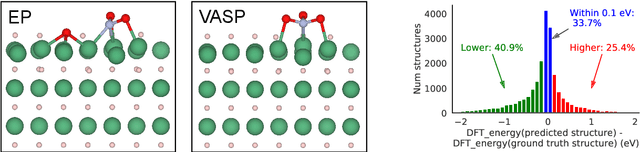
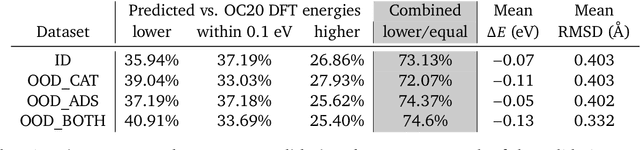
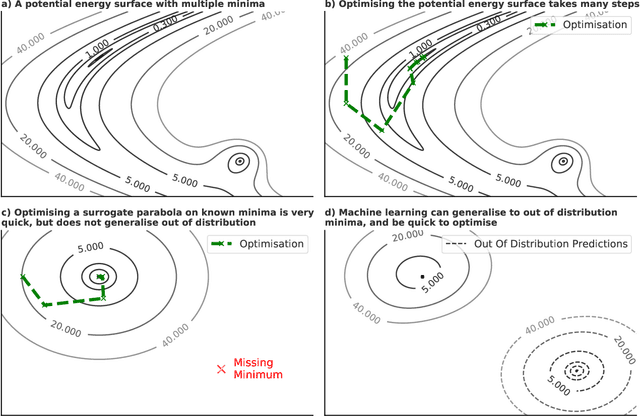
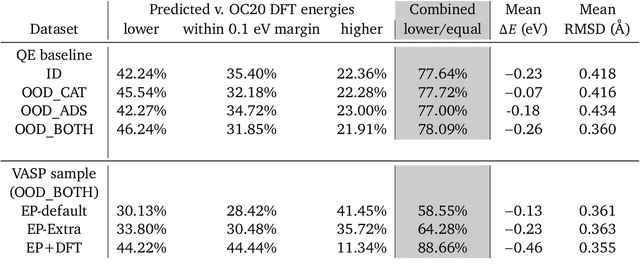
We present evidence that learned density functional theory (``DFT'') force fields are ready for ground state catalyst discovery. Our key finding is that relaxation using forces from a learned potential yields structures with similar or lower energy to those relaxed using the RPBE functional in over 50\% of evaluated systems, despite the fact that the predicted forces differ significantly from the ground truth. This has the surprising implication that learned potentials may be ready for replacing DFT in challenging catalytic systems such as those found in the Open Catalyst 2020 dataset. Furthermore, we show that a force field trained on a locally harmonic energy surface with the same minima as a target DFT energy is also able to find lower or similar energy structures in over 50\% of cases. This ``Easy Potential'' converges in fewer steps than a standard model trained on true energies and forces, which further accelerates calculations. Its success illustrates a key point: learned potentials can locate energy minima even when the model has high force errors. The main requirement for structure optimisation is simply that the learned potential has the correct minima. Since learned potentials are fast and scale linearly with system size, our results open the possibility of quickly finding ground states for large systems.

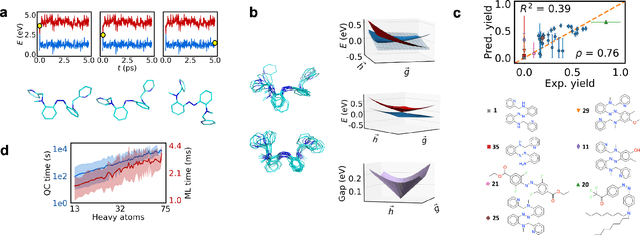
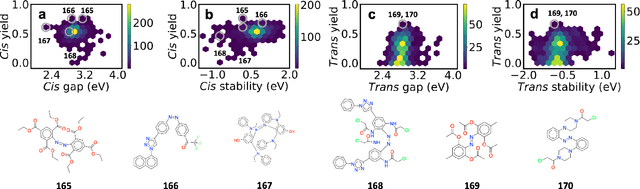
Thermal half-lives of azobenzene derivatives: virtual screening based on intersystem crossing using a machine learning potential

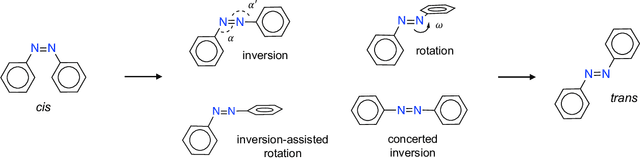
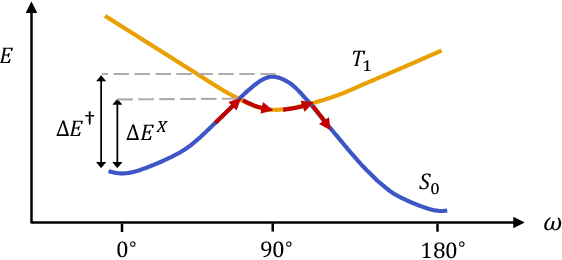
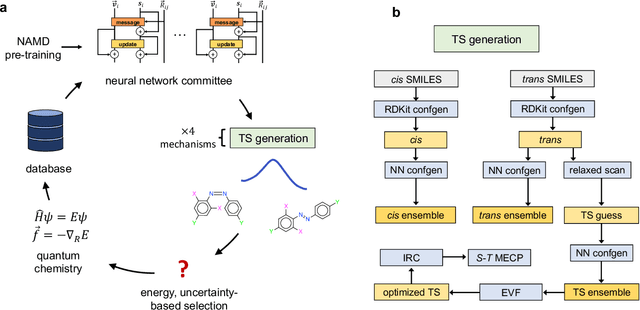
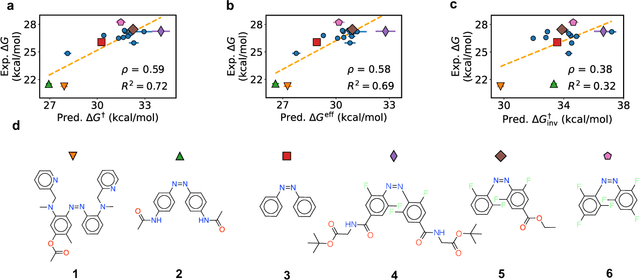
Molecular photoswitches are the foundation of light-activated drugs. A key photoswitch is azobenzene, which exhibits trans-cis isomerism in response to light. The thermal half-life of the cis isomer is of crucial importance, since it controls the duration of the light-induced biological effect. Here we introduce a computational tool for predicting the thermal half-lives of azobenzene derivatives. Our automated approach uses a fast and accurate machine learning potential trained on quantum chemistry data. Building on well-established earlier evidence, we argue that thermal isomerization proceeds through rotation mediated by intersystem crossing, and incorporate this mechanism into our automated workflow. We use our approach to predict the thermal half-lives of 19,000 azobenzene derivatives. We explore trends and tradeoffs between barriers and absorption wavelengths, and open-source our data and software to accelerate research in photopharmacology.

Excited state, non-adiabatic dynamics of large photoswitchable molecules using a chemically transferable machine learning potential

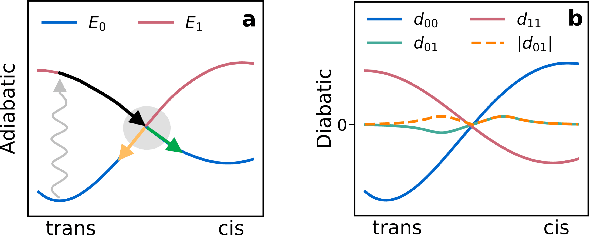
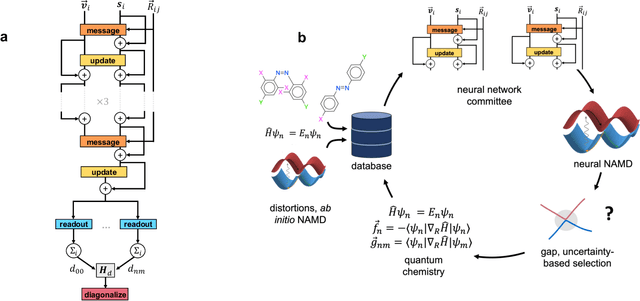
Light-induced chemical processes are ubiquitous in nature and have widespread technological applications. For example, the photoisomerization of azobenzene allows a drug with an azo scaffold to be activated with light. In principle, photoswitches with useful reactive properties, such as high isomerization yields, can be identified through virtual screening with reactive simulations. In practice these simulations are rarely used for screening, since they require hundreds of trajectories and expensive quantum chemical methods to account for non-adiabatic excited state effects. Here we introduce a neural network potential to accelerate such simulations for azobenzene derivatives. The model, which is based on diabatic states, is called the \textit{diabatic artificial neural network} (DANN). The network is six orders of magnitude faster than the quantum chemistry method used for training. DANN is transferable to molecules outside the training set, predicting quantum yields for unseen species that are correlated with experiment. We use the model to virtually screen 3,100 hypothetical molecules, and identify several species with extremely high quantum yields. Our results pave the way for fast and accurate virtual screening of photoactive compounds.

Molecular machine learning with conformer ensembles

Virtual screening can accelerate drug discovery by identifying top candidates for experimental testing. Machine learning is a powerful method for screening, as it can learn complex structure-property relationships from experimental data and make rapid predictions over virtual libraries. Although molecules are inherently three-dimensional and their biological action typically occurs through supramolecular recognition, most machine learning approaches use a 2D graph representation of molecules as input; few use 3D information, and none take into account the ensemble of conformers accessible to a species. Here we investigate whether the 3D information of multiple conformers can improve molecular property prediction. We introduce a number of new 3D-based models that can take multiple conformers as input to predict drug activity, and find that they learn interpretable weights for each conformer. The new architectures perform significantly better than 2D models, but their performance is just as strong with a single conformer as with many. From this analysis we identify the best 3D architecture and examine its predictions on species without experimental data.

GEOM: Energy-annotated molecular conformations for property prediction and molecular generation

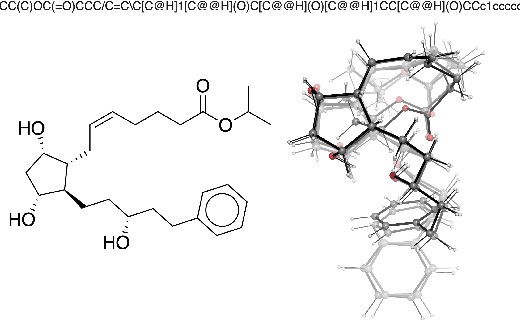
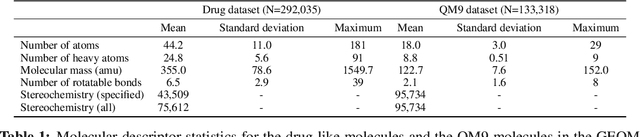
Machine learning outperforms traditional approaches in many molecular design tasks. Although molecules are often thought of as 2D graphs, they in fact consist of an ensemble of inter-converting 3D structures called conformers. Molecular properties arise from the contribution of many conformers, and in the case of a drug binding a target, may be due mainly to a few distinct members. Molecular representations in machine learning are typically based on either one single 3D conformer or on a 2D graph that strips geometrical information. No reference datasets exist that connect these graph and point cloud ensemble representations. Here, we use first-principles simulations to annotate over 400,000 molecules with the ensemble of geometries they span. The Geometrical Embedding Of Molecules (GEOM) dataset contains over 33 million molecular conformers labeled with their relative energies and statistical probabilities at room temperature. This dataset will assist benchmarking and transfer learning in two classes of tasks: inferring 3D properties from 2D molecular graphs, and developing generative models to sample 3D conformations.

Differentiable Molecular Simulations for Control and Learning

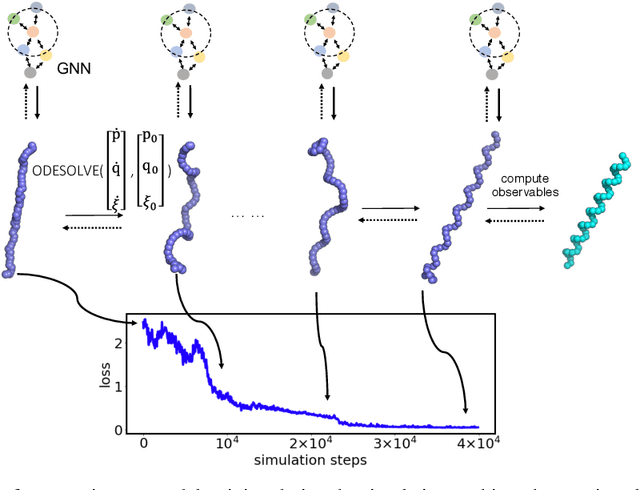
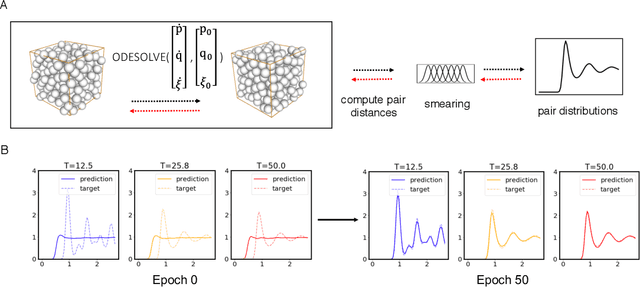
Molecular dynamics simulations use statistical mechanics at the atomistic scale to enable both the elucidation of fundamental mechanisms and the engineering of matter for desired tasks. The behavior of molecular systems at the microscale is typically simulated with differential equations parameterized by a Hamiltonian, or energy function. The Hamiltonian describes the state of the system and its interactions with the environment. In order to derive predictive microscopic models, one wishes to infer a molecular Hamiltonian that agrees with observed macroscopic quantities. From the perspective of engineering, one wishes to control the Hamiltonian to achieve desired simulation outcomes and structures, as in self-assembly and optical control, to then realize systems with the desired Hamiltonian in the lab. In both cases, the goal is to modify the Hamiltonian such that emergent properties of the simulated system match a given target. We demonstrate how this can be achieved using differentiable simulations where bulk target observables and simulation outcomes can be analytically differentiated with respect to Hamiltonians, opening up new routes for parameterizing Hamiltonians to infer macroscopic models and develop control protocols.