Forces are not Enough: Benchmark and Critical Evaluation for Machine Learning Force Fields with Molecular Simulations

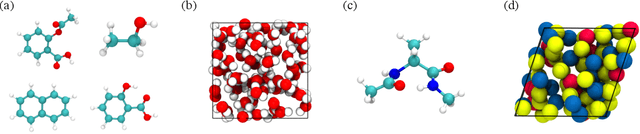
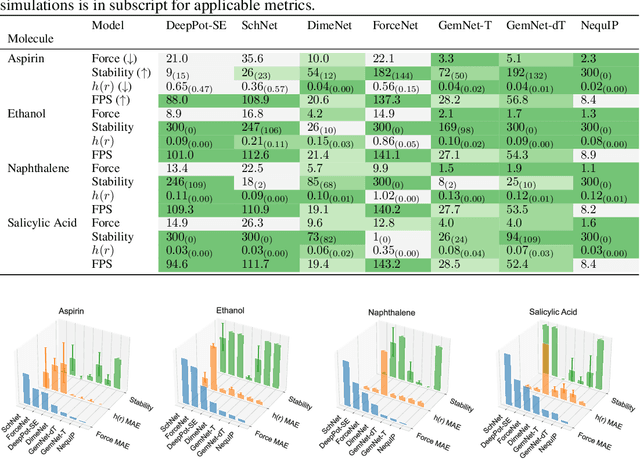
Molecular dynamics (MD) simulation techniques are widely used for various natural science applications. Increasingly, machine learning (ML) force field (FF) models begin to replace ab-initio simulations by predicting forces directly from atomic structures. Despite significant progress in this area, such techniques are primarily benchmarked by their force/energy prediction errors, even though the practical use case would be to produce realistic MD trajectories. We aim to fill this gap by introducing a novel benchmark suite for ML MD simulation. We curate representative MD systems, including water, organic molecules, peptide, and materials, and design evaluation metrics corresponding to the scientific objectives of respective systems. We benchmark a collection of state-of-the-art (SOTA) ML FF models and illustrate, in particular, how the commonly benchmarked force accuracy is not well aligned with relevant simulation metrics. We demonstrate when and how selected SOTA methods fail, along with offering directions for further improvement. Specifically, we identify stability as a key metric for ML models to improve. Our benchmark suite comes with a comprehensive open-source codebase for training and simulation with ML FFs to facilitate further work.

Learning Pair Potentials using Differentiable Simulations

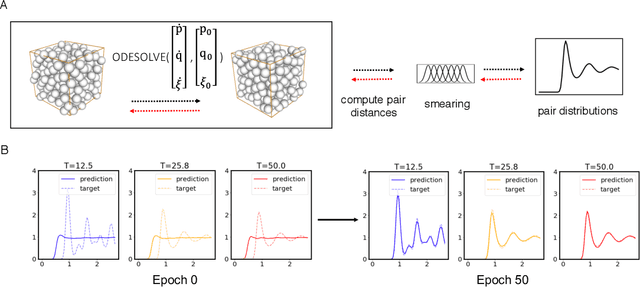
Learning pair interactions from experimental or simulation data is of great interest for molecular simulations. We propose a general stochastic method for learning pair interactions from data using differentiable simulations (DiffSim). DiffSim defines a loss function based on structural observables, such as the radial distribution function, through molecular dynamics (MD) simulations. The interaction potentials are then learned directly by stochastic gradient descent, using backpropagation to calculate the gradient of the structural loss metric with respect to the interaction potential through the MD simulation. This gradient-based method is flexible and can be configured to simulate and optimize multiple systems simultaneously. For example, it is possible to simultaneously learn potentials for different temperatures or for different compositions. We demonstrate the approach by recovering simple pair potentials, such as Lennard-Jones systems, from radial distribution functions. We find that DiffSim can be used to probe a wider functional space of pair potentials compared to traditional methods like Iterative Boltzmann Inversion. We show that our methods can be used to simultaneously fit potentials for simulations at different compositions and temperatures to improve the transferability of the learned potentials.

Generative Coarse-Graining of Molecular Conformations

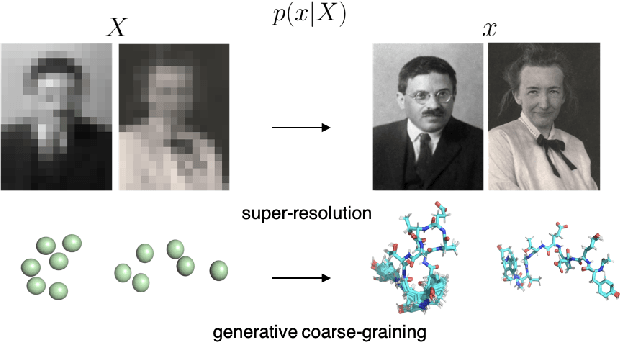
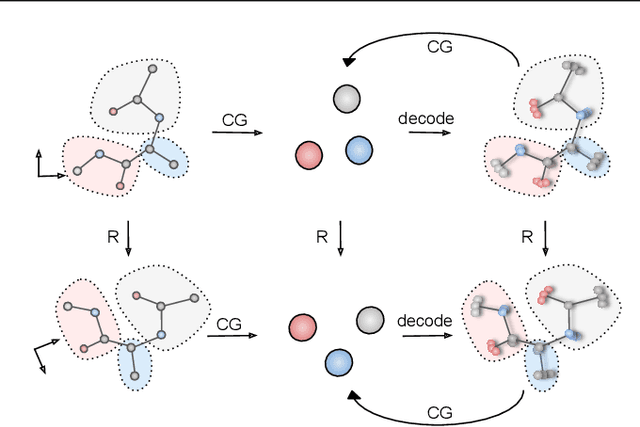
Coarse-graining (CG) of molecular simulations simplifies the particle representation by grouping selected atoms into pseudo-beads and therefore drastically accelerates simulation. However, such CG procedure induces information losses, which makes accurate backmapping, i.e., restoring fine-grained (FG) coordinates from CG coordinates, a long-standing challenge. Inspired by the recent progress in generative models and equivariant networks, we propose a novel model that rigorously embeds the vital probabilistic nature and geometric consistency requirements of the backmapping transformation. Our model encodes the FG uncertainties into an invariant latent space and decodes them back to FG geometries via equivariant convolutions. To standardize the evaluation of this domain, we further provide three comprehensive benchmarks based on molecular dynamics trajectories. Extensive experiments show that our approach always recovers more realistic structures and outperforms existing data-driven methods with a significant margin.

An End-to-End Framework for Molecular Conformation Generation via Bilevel Programming

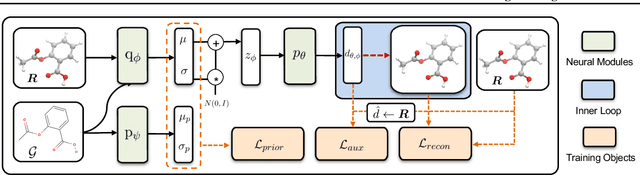
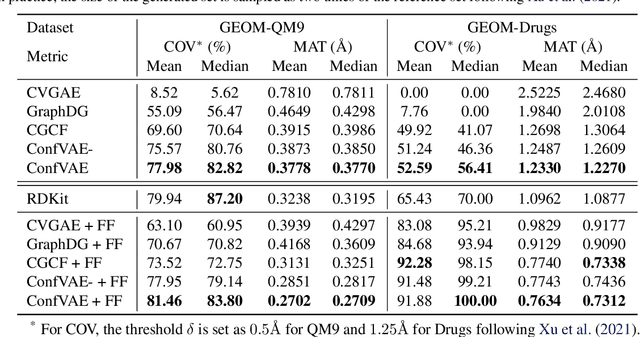
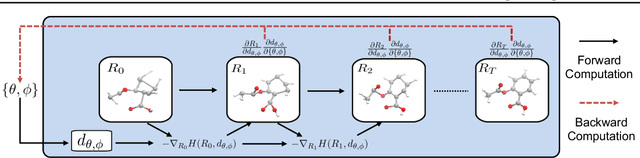
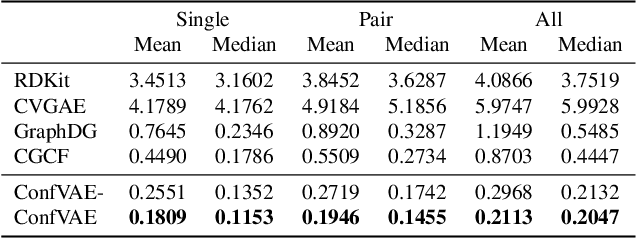
Predicting molecular conformations (or 3D structures) from molecular graphs is a fundamental problem in many applications. Most existing approaches are usually divided into two steps by first predicting the distances between atoms and then generating a 3D structure through optimizing a distance geometry problem. However, the distances predicted with such two-stage approaches may not be able to consistently preserve the geometry of local atomic neighborhoods, making the generated structures unsatisfying. In this paper, we propose an end-to-end solution for molecular conformation prediction called ConfVAE based on the conditional variational autoencoder framework. Specifically, the molecular graph is first encoded in a latent space, and then the 3D structures are generated by solving a principled bilevel optimization program. Extensive experiments on several benchmark data sets prove the effectiveness of our proposed approach over existing state-of-the-art approaches. Code is available at \url{https://github.com/MinkaiXu/ConfVAE-ICML21}.

Differentiable Molecular Simulations for Control and Learning

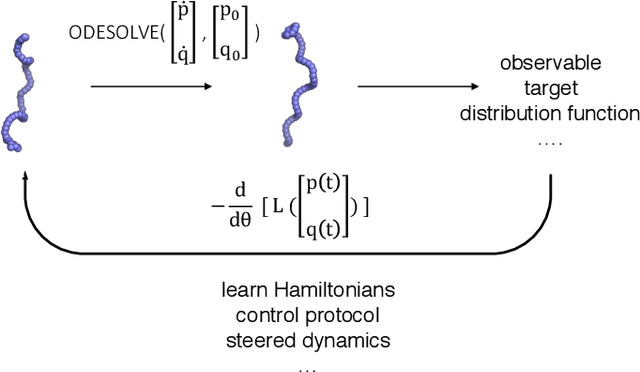
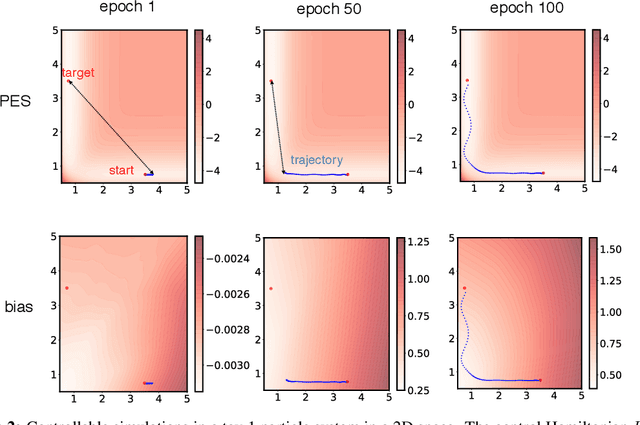
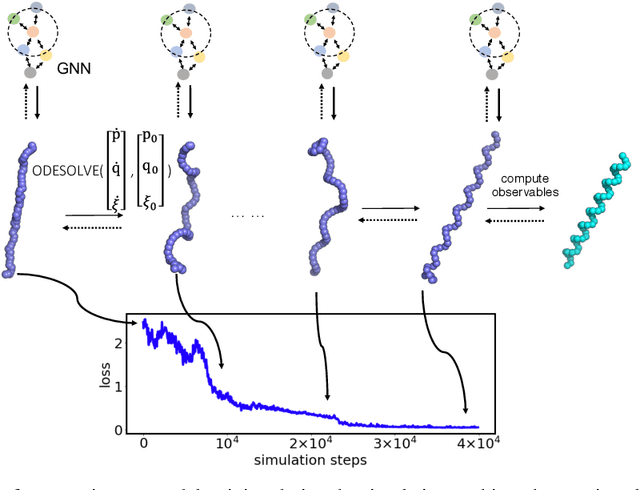
Molecular dynamics simulations use statistical mechanics at the atomistic scale to enable both the elucidation of fundamental mechanisms and the engineering of matter for desired tasks. The behavior of molecular systems at the microscale is typically simulated with differential equations parameterized by a Hamiltonian, or energy function. The Hamiltonian describes the state of the system and its interactions with the environment. In order to derive predictive microscopic models, one wishes to infer a molecular Hamiltonian that agrees with observed macroscopic quantities. From the perspective of engineering, one wishes to control the Hamiltonian to achieve desired simulation outcomes and structures, as in self-assembly and optical control, to then realize systems with the desired Hamiltonian in the lab. In both cases, the goal is to modify the Hamiltonian such that emergent properties of the simulated system match a given target. We demonstrate how this can be achieved using differentiable simulations where bulk target observables and simulation outcomes can be analytically differentiated with respect to Hamiltonians, opening up new routes for parameterizing Hamiltonians to infer macroscopic models and develop control protocols.

Variational Coarse-Graining for Molecular Dynamics

Molecular dynamics simulations provide theoretical insight into the microscopic behavior of materials in condensed phase and, as a predictive tool, enable computational design of new compounds. However, because of the large temporal and spatial scales involved in thermodynamic and kinetic phenomena in materials, atomistic simulations are often computationally unfeasible. Coarse-graining methods allow simulating larger systems, by reducing the dimensionality of the simulation, and propagating longer timesteps, by averaging out fast motions. Coarse-graining involves two coupled learning problems; defining the mapping from an all-atom to a reduced representation, and parametrizing a Hamiltonian over coarse-grained coordinates. Multiple statistical mechanics approaches have addressed the latter, but the former is generally a hand-tuned process based on chemical intuition. Here we present Autograin, an optimization framework based on auto-encoders to learn both tasks simultaneously. Autograin automatically learns the optimal mapping between all-atom and reduced representation, using the reconstruction loss to facilitate the learning of coarse-grained variables. In addition, a force-matching method is applied to variationally determine the coarse-grained potential energy function. This procedure is tested on a number of model systems including single-molecule and bulk-phase periodic simulations.