Generative Coarse-Graining of Molecular Conformations

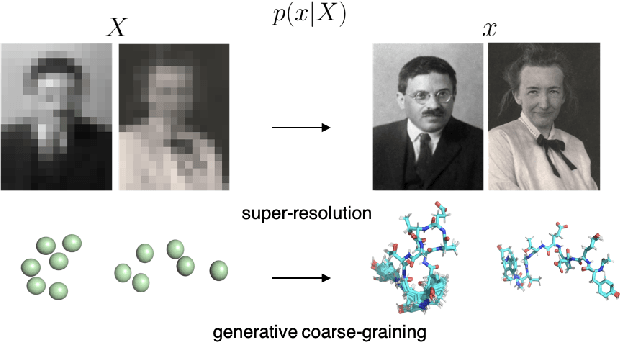
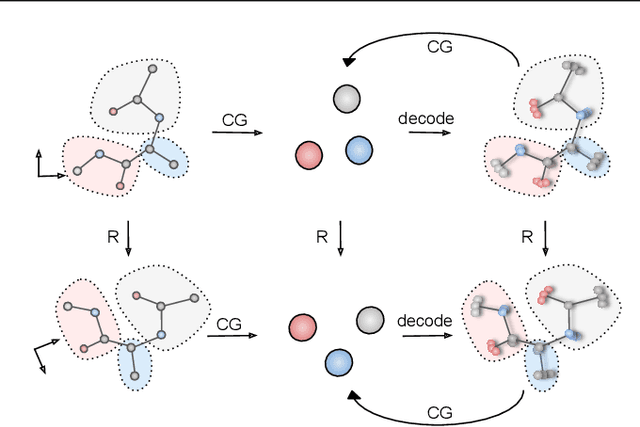
Coarse-graining (CG) of molecular simulations simplifies the particle representation by grouping selected atoms into pseudo-beads and therefore drastically accelerates simulation. However, such CG procedure induces information losses, which makes accurate backmapping, i.e., restoring fine-grained (FG) coordinates from CG coordinates, a long-standing challenge. Inspired by the recent progress in generative models and equivariant networks, we propose a novel model that rigorously embeds the vital probabilistic nature and geometric consistency requirements of the backmapping transformation. Our model encodes the FG uncertainties into an invariant latent space and decodes them back to FG geometries via equivariant convolutions. To standardize the evaluation of this domain, we further provide three comprehensive benchmarks based on molecular dynamics trajectories. Extensive experiments show that our approach always recovers more realistic structures and outperforms existing data-driven methods with a significant margin.