sbi reloaded: a toolkit for simulation-based inference workflows

Scientists and engineers use simulators to model empirically observed phenomena. However, tuning the parameters of a simulator to ensure its outputs match observed data presents a significant challenge. Simulation-based inference (SBI) addresses this by enabling Bayesian inference for simulators, identifying parameters that match observed data and align with prior knowledge. Unlike traditional Bayesian inference, SBI only needs access to simulations from the model and does not require evaluations of the likelihood-function. In addition, SBI algorithms do not require gradients through the simulator, allow for massive parallelization of simulations, and can perform inference for different observations without further simulations or training, thereby amortizing inference. Over the past years, we have developed, maintained, and extended $\texttt{sbi}$, a PyTorch-based package that implements Bayesian SBI algorithms based on neural networks. The $\texttt{sbi}$ toolkit implements a wide range of inference methods, neural network architectures, sampling methods, and diagnostic tools. In addition, it provides well-tested default settings but also offers flexibility to fully customize every step of the simulation-based inference workflow. Taken together, the $\texttt{sbi}$ toolkit enables scientists and engineers to apply state-of-the-art SBI methods to black-box simulators, opening up new possibilities for aligning simulations with empirically observed data.

FlowLLM: Flow Matching for Material Generation with Large Language Models as Base Distributions

Material discovery is a critical area of research with the potential to revolutionize various fields, including carbon capture, renewable energy, and electronics. However, the immense scale of the chemical space makes it challenging to explore all possible materials experimentally. In this paper, we introduce FlowLLM, a novel generative model that combines large language models (LLMs) and Riemannian flow matching (RFM) to design novel crystalline materials. FlowLLM first fine-tunes an LLM to learn an effective base distribution of meta-stable crystals in a text representation. After converting to a graph representation, the RFM model takes samples from the LLM and iteratively refines the coordinates and lattice parameters. Our approach significantly outperforms state-of-the-art methods, increasing the generation rate of stable materials by over three times and increasing the rate for stable, unique, and novel crystals by $\sim50\%$ - a huge improvement on a difficult problem. Additionally, the crystals generated by FlowLLM are much closer to their relaxed state when compared with another leading model, significantly reducing post-hoc computational cost.

FlowMM: Generating Materials with Riemannian Flow Matching

Crystalline materials are a fundamental component in next-generation technologies, yet modeling their distribution presents unique computational challenges. Of the plausible arrangements of atoms in a periodic lattice only a vanishingly small percentage are thermodynamically stable, which is a key indicator of the materials that can be experimentally realized. Two fundamental tasks in this area are to (a) predict the stable crystal structure of a known composition of elements and (b) propose novel compositions along with their stable structures. We present FlowMM, a pair of generative models that achieve state-of-the-art performance on both tasks while being more efficient and more flexible than competing methods. We generalize Riemannian Flow Matching to suit the symmetries inherent to crystals: translation, rotation, permutation, and periodic boundary conditions. Our framework enables the freedom to choose the flow base distributions, drastically simplifying the problem of learning crystal structures compared with diffusion models. In addition to standard benchmarks, we validate FlowMM's generated structures with quantum chemistry calculations, demonstrating that it is about 3x more efficient, in terms of integration steps, at finding stable materials compared to previous open methods.

Simulation-based Inference with the Generalized Kullback-Leibler Divergence

In Simulation-based Inference, the goal is to solve the inverse problem when the likelihood is only known implicitly. Neural Posterior Estimation commonly fits a normalized density estimator as a surrogate model for the posterior. This formulation cannot easily fit unnormalized surrogates because it optimizes the Kullback-Leibler divergence. We propose to optimize a generalized Kullback-Leibler divergence that accounts for the normalization constant in unnormalized distributions. The objective recovers Neural Posterior Estimation when the model class is normalized and unifies it with Neural Ratio Estimation, combining both into a single objective. We investigate a hybrid model that offers the best of both worlds by learning a normalized base distribution and a learned ratio. We also present benchmark results.

Balancing Simulation-based Inference for Conservative Posteriors

Conservative inference is a major concern in simulation-based inference. It has been shown that commonly used algorithms can produce overconfident posterior approximations. Balancing has empirically proven to be an effective way to mitigate this issue. However, its application remains limited to neural ratio estimation. In this work, we extend balancing to any algorithm that provides a posterior density. In particular, we introduce a balanced version of both neural posterior estimation and contrastive neural ratio estimation. We show empirically that the balanced versions tend to produce conservative posterior approximations on a wide variety of benchmarks. In addition, we provide an alternative interpretation of the balancing condition in terms of the $\chi^2$ divergence.

Contrastive Neural Ratio Estimation

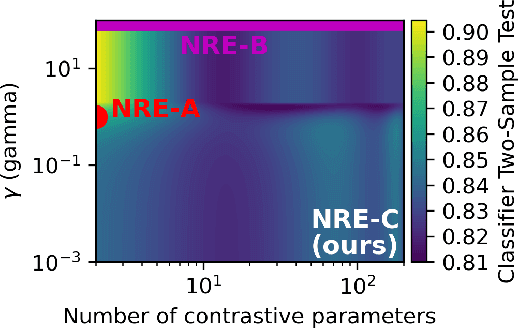
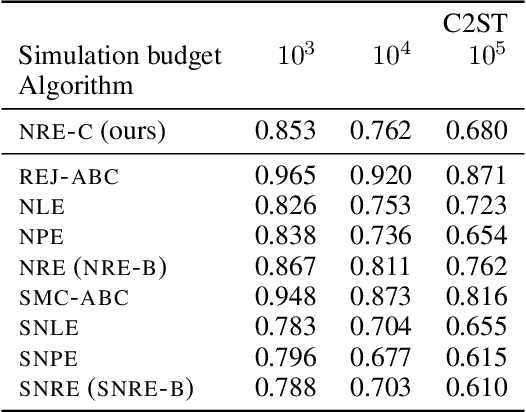
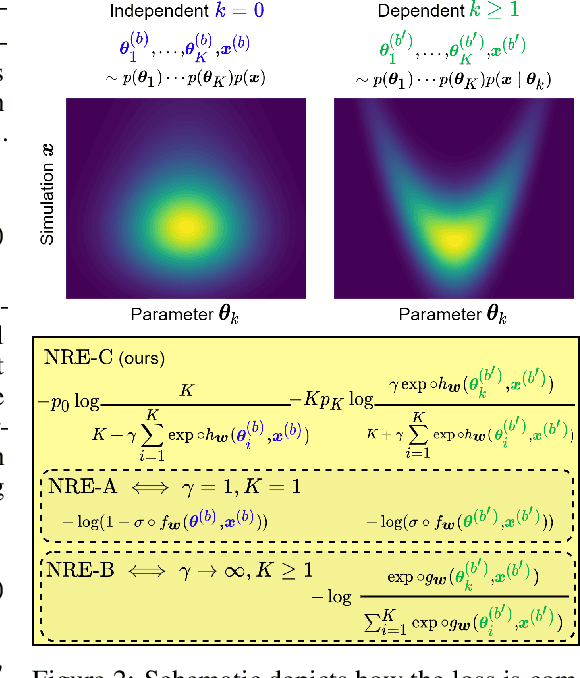
Likelihood-to-evidence ratio estimation is usually cast as either a binary (NRE-A) or a multiclass (NRE-B) classification task. In contrast to the binary classification framework, the current formulation of the multiclass version has an intrinsic and unknown bias term, making otherwise informative diagnostics unreliable. We propose a multiclass framework free from the bias inherent to NRE-B at optimum, leaving us in the position to run diagnostics that practitioners depend on. It also recovers NRE-A in one corner case and NRE-B in the limiting case. For fair comparison, we benchmark the behavior of all algorithms in both familiar and novel training regimes: when jointly drawn data is unlimited, when data is fixed but prior draws are unlimited, and in the commonplace fixed data and parameters setting. Our investigations reveal that the highest performing models are distant from the competitors (NRE-A, NRE-B) in hyperparameter space. We make a recommendation for hyperparameters distinct from the previous models. We suggest a bound on the mutual information as a performance metric for simulation-based inference methods, without the need for posterior samples, and provide experimental results.

Generative Coarse-Graining of Molecular Conformations

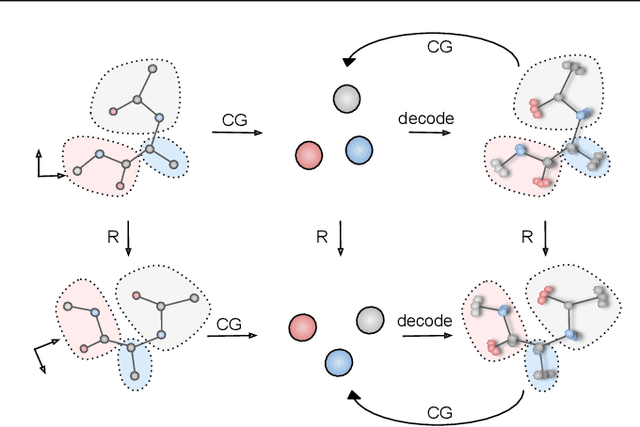
Coarse-graining (CG) of molecular simulations simplifies the particle representation by grouping selected atoms into pseudo-beads and therefore drastically accelerates simulation. However, such CG procedure induces information losses, which makes accurate backmapping, i.e., restoring fine-grained (FG) coordinates from CG coordinates, a long-standing challenge. Inspired by the recent progress in generative models and equivariant networks, we propose a novel model that rigorously embeds the vital probabilistic nature and geometric consistency requirements of the backmapping transformation. Our model encodes the FG uncertainties into an invariant latent space and decodes them back to FG geometries via equivariant convolutions. To standardize the evaluation of this domain, we further provide three comprehensive benchmarks based on molecular dynamics trajectories. Extensive experiments show that our approach always recovers more realistic structures and outperforms existing data-driven methods with a significant margin.

Automatically detecting anomalous exoplanet transits

Raw light curve data from exoplanet transits is too complex to naively apply traditional outlier detection methods. We propose an architecture which estimates a latent representation of both the main transit and residual deviations with a pair of variational autoencoders. We show, using two fabricated datasets, that our latent representations of anomalous transit residuals are significantly more amenable to outlier detection than raw data or the latent representation of a traditional variational autoencoder. We then apply our method to real exoplanet transit data. Our study is the first which automatically identifies anomalous exoplanet transit light curves. We additionally release three first-of-their-kind datasets to enable further research.

Fast and Credible Likelihood-Free Cosmology with Truncated Marginal Neural Ratio Estimation

Sampling-based inference techniques are central to modern cosmological data analysis; these methods, however, scale poorly with dimensionality and typically require approximate or intractable likelihoods. In this paper we describe how Truncated Marginal Neural Ratio Estimation (TMNRE) (a new approach in so-called simulation-based inference) naturally evades these issues, improving the $(i)$ efficiency, $(ii)$ scalability, and $(iii)$ trustworthiness of the inferred posteriors. Using measurements of the Cosmic Microwave Background (CMB), we show that TMNRE can achieve converged posteriors using orders of magnitude fewer simulator calls than conventional Markov Chain Monte Carlo (MCMC) methods. Remarkably, the required number of samples is effectively independent of the number of nuisance parameters. In addition, a property called \emph{local amortization} allows the performance of rigorous statistical consistency checks that are not accessible to sampling-based methods. TMNRE promises to become a powerful tool for cosmological data analysis, particularly in the context of extended cosmologies, where the timescale required for conventional sampling-based inference methods to converge can greatly exceed that of simple cosmological models such as $\Lambda$CDM. To perform these computations, we use an implementation of TMNRE via the open-source code \texttt{swyft}.

Truncated Marginal Neural Ratio Estimation

Parametric stochastic simulators are ubiquitous in science, often featuring high-dimensional input parameters and/or an intractable likelihood. Performing Bayesian parameter inference in this context can be challenging. We present a neural simulator-based inference algorithm which simultaneously offers simulation efficiency and fast empirical posterior testability, which is unique among modern algorithms. Our approach is simulation efficient by simultaneously estimating low-dimensional marginal posteriors instead of the joint posterior and by proposing simulations targeted to an observation of interest via a prior suitably truncated by an indicator function. Furthermore, by estimating a locally amortized posterior our algorithm enables efficient empirical tests of the robustness of the inference results. Such tests are important for sanity-checking inference in real-world applications, which do not feature a known ground truth. We perform experiments on a marginalized version of the simulation-based inference benchmark and two complex and narrow posteriors, highlighting the simulator efficiency of our algorithm as well as the quality of the estimated marginal posteriors. Implementation on GitHub.