Fast Sampling of Cosmological Initial Conditions with Gaussian Neural Posterior Estimation

Knowledge of the primordial matter density field from which the large-scale structure of the Universe emerged over cosmic time is of fundamental importance for cosmology. However, reconstructing these cosmological initial conditions from late-time observations is a notoriously difficult task, which requires advanced cosmological simulators and sophisticated statistical methods to explore a multi-million-dimensional parameter space. We show how simulation-based inference (SBI) can be used to tackle this problem and to obtain data-constrained realisations of the primordial dark matter density field in a simulation-efficient way with general non-differentiable simulators. Our method is applicable to full high-resolution dark matter $N$-body simulations and is based on modelling the posterior distribution of the constrained initial conditions to be Gaussian with a diagonal covariance matrix in Fourier space. As a result, we can generate thousands of posterior samples within seconds on a single GPU, orders of magnitude faster than existing methods, paving the way for sequential SBI for cosmological fields. Furthermore, we perform an analytical fit of the estimated dependence of the covariance on the wavenumber, effectively transforming any point-estimator of initial conditions into a fast sampler. We test the validity of our obtained samples by comparing them to the true values with summary statistics and performing a Bayesian consistency test.

Large Physics Models: Towards a collaborative approach with Large Language Models and Foundation Models

This paper explores ideas and provides a potential roadmap for the development and evaluation of physics-specific large-scale AI models, which we call Large Physics Models (LPMs). These models, based on foundation models such as Large Language Models (LLMs) - trained on broad data - are tailored to address the demands of physics research. LPMs can function independently or as part of an integrated framework. This framework can incorporate specialized tools, including symbolic reasoning modules for mathematical manipulations, frameworks to analyse specific experimental and simulated data, and mechanisms for synthesizing theories and scientific literature. We begin by examining whether the physics community should actively develop and refine dedicated models, rather than relying solely on commercial LLMs. We then outline how LPMs can be realized through interdisciplinary collaboration among experts in physics, computer science, and philosophy of science. To integrate these models effectively, we identify three key pillars: Development, Evaluation, and Philosophical Reflection. Development focuses on constructing models capable of processing physics texts, mathematical formulations, and diverse physical data. Evaluation assesses accuracy and reliability by testing and benchmarking. Finally, Philosophical Reflection encompasses the analysis of broader implications of LLMs in physics, including their potential to generate new scientific understanding and what novel collaboration dynamics might arise in research. Inspired by the organizational structure of experimental collaborations in particle physics, we propose a similarly interdisciplinary and collaborative approach to building and refining Large Physics Models. This roadmap provides specific objectives, defines pathways to achieve them, and identifies challenges that must be addressed to realise physics-specific large scale AI models.

Tests for model misspecification in simulation-based inference: from local distortions to global model checks

Model misspecification analysis strategies, such as anomaly detection, model validation, and model comparison are a key component of scientific model development. Over the last few years, there has been a rapid rise in the use of simulation-based inference (SBI) techniques for Bayesian parameter estimation, applied to increasingly complex forward models. To move towards fully simulation-based analysis pipelines, however, there is an urgent need for a comprehensive simulation-based framework for model misspecification analysis. In this work, we provide a solid and flexible foundation for a wide range of model discrepancy analysis tasks, using distortion-driven model misspecification tests. From a theoretical perspective, we introduce the statistical framework built around performing many hypothesis tests for distortions of the simulation model. We also make explicit analytic connections to classical techniques: anomaly detection, model validation, and goodness-of-fit residual analysis. Furthermore, we introduce an efficient self-calibrating training algorithm that is useful for practitioners. We demonstrate the performance of the framework in multiple scenarios, making the connection to classical results where they are valid. Finally, we show how to conduct such a distortion-driven model misspecification test for real gravitational wave data, specifically on the event GW150914.

Mean-Field Simulation-Based Inference for Cosmological Initial Conditions

Reconstructing cosmological initial conditions (ICs) from late-time observations is a difficult task, which relies on the use of computationally expensive simulators alongside sophisticated statistical methods to navigate multi-million dimensional parameter spaces. We present a simple method for Bayesian field reconstruction based on modeling the posterior distribution of the initial matter density field to be diagonal Gaussian in Fourier space, with its covariance and the mean estimator being the trainable parts of the algorithm. Training and sampling are extremely fast (training: $\sim 1 \, \mathrm{h}$ on a GPU, sampling: $\lesssim 3 \, \mathrm{s}$ for 1000 samples at resolution $128^3$), and our method supports industry-standard (non-differentiable) $N$-body simulators. We verify the fidelity of the obtained IC samples in terms of summary statistics.

Bayesian Simulation-based Inference for Cosmological Initial Conditions

Reconstructing astrophysical and cosmological fields from observations is challenging. It requires accounting for non-linear transformations, mixing of spatial structure, and noise. In contrast, forward simulators that map fields to observations are readily available for many applications. We present a versatile Bayesian field reconstruction algorithm rooted in simulation-based inference and enhanced by autoregressive modeling. The proposed technique is applicable to generic (non-differentiable) forward simulators and allows sampling from the posterior for the underlying field. We show first promising results on a proof-of-concept application: the recovery of cosmological initial conditions from late-time density fields.

Simulation-based Inference with the Generalized Kullback-Leibler Divergence

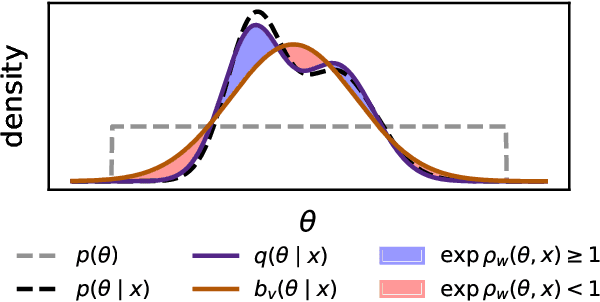
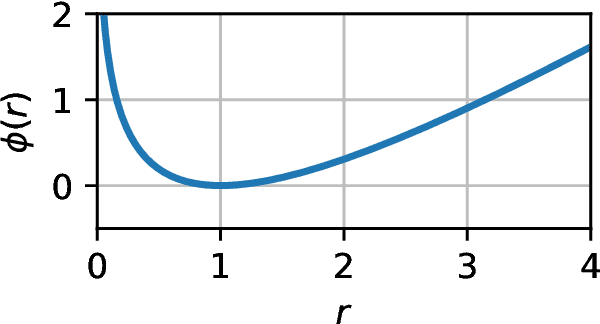
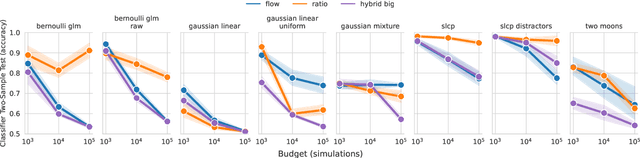
In Simulation-based Inference, the goal is to solve the inverse problem when the likelihood is only known implicitly. Neural Posterior Estimation commonly fits a normalized density estimator as a surrogate model for the posterior. This formulation cannot easily fit unnormalized surrogates because it optimizes the Kullback-Leibler divergence. We propose to optimize a generalized Kullback-Leibler divergence that accounts for the normalization constant in unnormalized distributions. The objective recovers Neural Posterior Estimation when the model class is normalized and unifies it with Neural Ratio Estimation, combining both into a single objective. We investigate a hybrid model that offers the best of both worlds by learning a normalized base distribution and a learned ratio. We also present benchmark results.

Balancing Simulation-based Inference for Conservative Posteriors

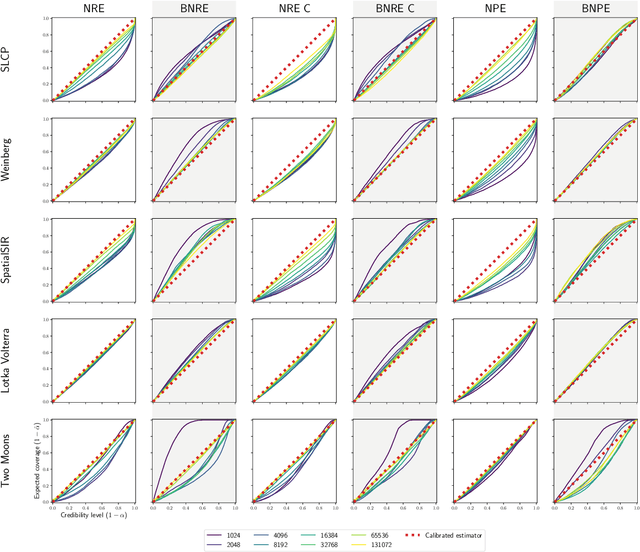
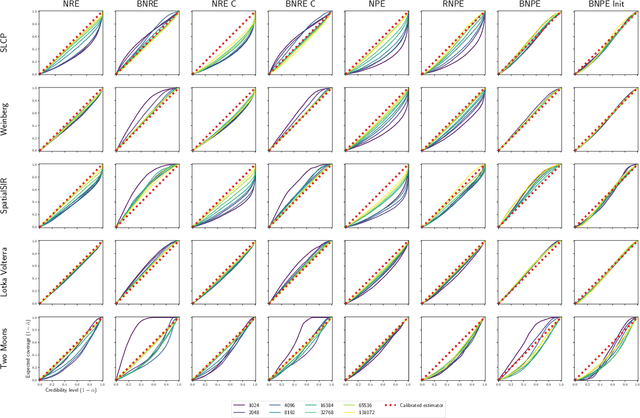
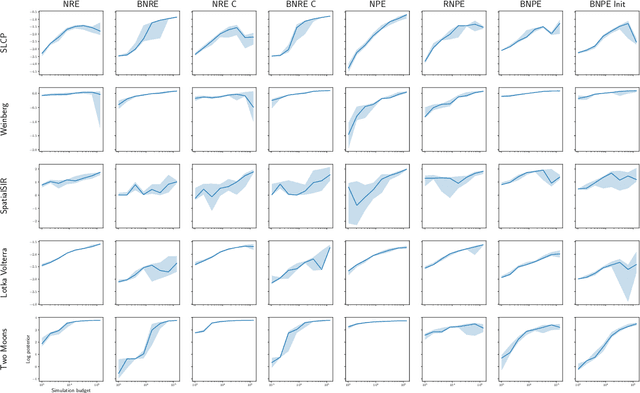
Conservative inference is a major concern in simulation-based inference. It has been shown that commonly used algorithms can produce overconfident posterior approximations. Balancing has empirically proven to be an effective way to mitigate this issue. However, its application remains limited to neural ratio estimation. In this work, we extend balancing to any algorithm that provides a posterior density. In particular, we introduce a balanced version of both neural posterior estimation and contrastive neural ratio estimation. We show empirically that the balanced versions tend to produce conservative posterior approximations on a wide variety of benchmarks. In addition, we provide an alternative interpretation of the balancing condition in terms of the $\chi^2$ divergence.

Contrastive Neural Ratio Estimation

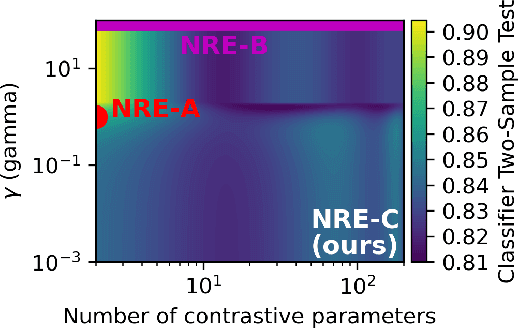
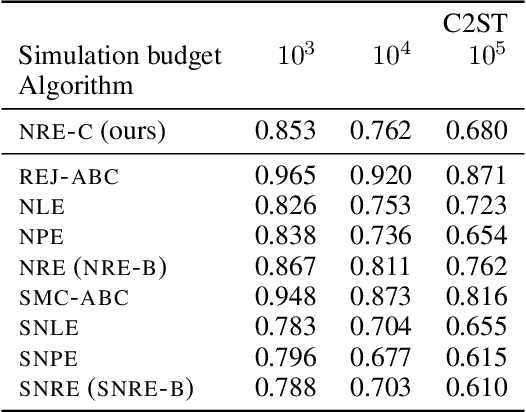
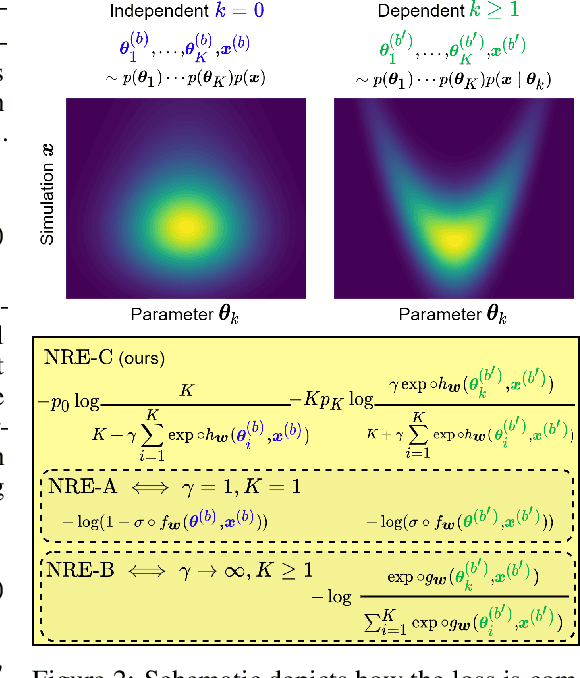
Likelihood-to-evidence ratio estimation is usually cast as either a binary (NRE-A) or a multiclass (NRE-B) classification task. In contrast to the binary classification framework, the current formulation of the multiclass version has an intrinsic and unknown bias term, making otherwise informative diagnostics unreliable. We propose a multiclass framework free from the bias inherent to NRE-B at optimum, leaving us in the position to run diagnostics that practitioners depend on. It also recovers NRE-A in one corner case and NRE-B in the limiting case. For fair comparison, we benchmark the behavior of all algorithms in both familiar and novel training regimes: when jointly drawn data is unlimited, when data is fixed but prior draws are unlimited, and in the commonplace fixed data and parameters setting. Our investigations reveal that the highest performing models are distant from the competitors (NRE-A, NRE-B) in hyperparameter space. We make a recommendation for hyperparameters distinct from the previous models. We suggest a bound on the mutual information as a performance metric for simulation-based inference methods, without the need for posterior samples, and provide experimental results.

Fast and Credible Likelihood-Free Cosmology with Truncated Marginal Neural Ratio Estimation

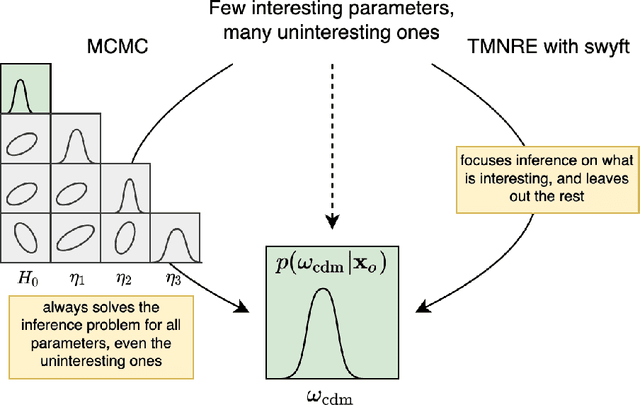
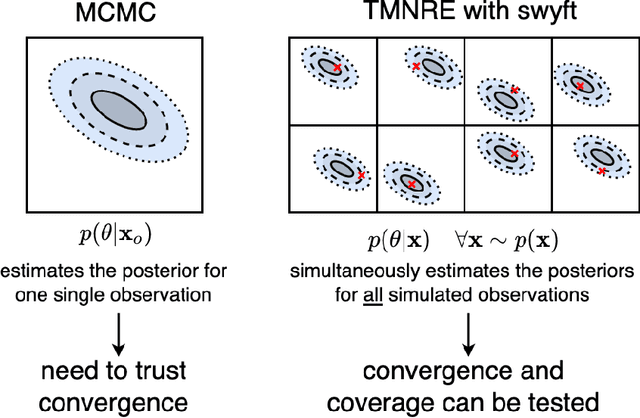
Sampling-based inference techniques are central to modern cosmological data analysis; these methods, however, scale poorly with dimensionality and typically require approximate or intractable likelihoods. In this paper we describe how Truncated Marginal Neural Ratio Estimation (TMNRE) (a new approach in so-called simulation-based inference) naturally evades these issues, improving the $(i)$ efficiency, $(ii)$ scalability, and $(iii)$ trustworthiness of the inferred posteriors. Using measurements of the Cosmic Microwave Background (CMB), we show that TMNRE can achieve converged posteriors using orders of magnitude fewer simulator calls than conventional Markov Chain Monte Carlo (MCMC) methods. Remarkably, the required number of samples is effectively independent of the number of nuisance parameters. In addition, a property called \emph{local amortization} allows the performance of rigorous statistical consistency checks that are not accessible to sampling-based methods. TMNRE promises to become a powerful tool for cosmological data analysis, particularly in the context of extended cosmologies, where the timescale required for conventional sampling-based inference methods to converge can greatly exceed that of simple cosmological models such as $\Lambda$CDM. To perform these computations, we use an implementation of TMNRE via the open-source code \texttt{swyft}.

Truncated Marginal Neural Ratio Estimation

Parametric stochastic simulators are ubiquitous in science, often featuring high-dimensional input parameters and/or an intractable likelihood. Performing Bayesian parameter inference in this context can be challenging. We present a neural simulator-based inference algorithm which simultaneously offers simulation efficiency and fast empirical posterior testability, which is unique among modern algorithms. Our approach is simulation efficient by simultaneously estimating low-dimensional marginal posteriors instead of the joint posterior and by proposing simulations targeted to an observation of interest via a prior suitably truncated by an indicator function. Furthermore, by estimating a locally amortized posterior our algorithm enables efficient empirical tests of the robustness of the inference results. Such tests are important for sanity-checking inference in real-world applications, which do not feature a known ground truth. We perform experiments on a marginalized version of the simulation-based inference benchmark and two complex and narrow posteriors, highlighting the simulator efficiency of our algorithm as well as the quality of the estimated marginal posteriors. Implementation on GitHub.