On the Energy Distribution of the Galactic Center Excess' Sources

The Galactic Center Excess (GCE) remains one of the defining mysteries uncovered by the Fermi $\gamma$-ray Space Telescope. Although it may yet herald the discovery of annihilating dark matter, weighing against that conclusion are analyses showing the spatial structure of the emission appears more consistent with a population of dim point sources. Technical limitations have restricted prior analyses to studying the point-source hypothesis purely spatially. All spectral information that could help disentangle the GCE from the complex and uncertain astrophysical emission was discarded. We demonstrate that a neural network-aided simulation-based inference approach can overcome such limitations and thereby confront the point source explanation of the GCE with spatial and spectral data. The addition is profound: energy information drives the putative point sources to be significantly dimmer, indicating either the GCE is truly diffuse in nature or made of an exceptionally large number of sources. Quantitatively, for our best fit background model, the excess is essentially consistent with Poisson emission as predicted by dark matter. If the excess is instead due to point sources, our median prediction is ${\cal O}(10^5)$ sources in the Galactic Center, or more than 35,000 sources at 90% confidence, both significantly larger than the hundreds of sources preferred by earlier point-source analyses of the GCE.

Fast Sampling of Cosmological Initial Conditions with Gaussian Neural Posterior Estimation

Knowledge of the primordial matter density field from which the large-scale structure of the Universe emerged over cosmic time is of fundamental importance for cosmology. However, reconstructing these cosmological initial conditions from late-time observations is a notoriously difficult task, which requires advanced cosmological simulators and sophisticated statistical methods to explore a multi-million-dimensional parameter space. We show how simulation-based inference (SBI) can be used to tackle this problem and to obtain data-constrained realisations of the primordial dark matter density field in a simulation-efficient way with general non-differentiable simulators. Our method is applicable to full high-resolution dark matter $N$-body simulations and is based on modelling the posterior distribution of the constrained initial conditions to be Gaussian with a diagonal covariance matrix in Fourier space. As a result, we can generate thousands of posterior samples within seconds on a single GPU, orders of magnitude faster than existing methods, paving the way for sequential SBI for cosmological fields. Furthermore, we perform an analytical fit of the estimated dependence of the covariance on the wavenumber, effectively transforming any point-estimator of initial conditions into a fast sampler. We test the validity of our obtained samples by comparing them to the true values with summary statistics and performing a Bayesian consistency test.

Mean-Field Simulation-Based Inference for Cosmological Initial Conditions

Reconstructing cosmological initial conditions (ICs) from late-time observations is a difficult task, which relies on the use of computationally expensive simulators alongside sophisticated statistical methods to navigate multi-million dimensional parameter spaces. We present a simple method for Bayesian field reconstruction based on modeling the posterior distribution of the initial matter density field to be diagonal Gaussian in Fourier space, with its covariance and the mean estimator being the trainable parts of the algorithm. Training and sampling are extremely fast (training: $\sim 1 \, \mathrm{h}$ on a GPU, sampling: $\lesssim 3 \, \mathrm{s}$ for 1000 samples at resolution $128^3$), and our method supports industry-standard (non-differentiable) $N$-body simulators. We verify the fidelity of the obtained IC samples in terms of summary statistics.

A deep learning framework for jointly extracting spectra and source-count distributions in astronomy

Astronomical observations typically provide three-dimensional maps, encoding the distribution of the observed flux in (1) the two angles of the celestial sphere and (2) energy/frequency. An important task regarding such maps is to statistically characterize populations of point sources too dim to be individually detected. As the properties of a single dim source will be poorly constrained, instead one commonly studies the population as a whole, inferring a source-count distribution (SCD) that describes the number density of sources as a function of their brightness. Statistical and machine learning methods for recovering SCDs exist; however, they typically entirely neglect spectral information associated with the energy distribution of the flux. We present a deep learning framework able to jointly reconstruct the spectra of different emission components and the SCD of point-source populations. In a proof-of-concept example, we show that our method accurately extracts even complex-shaped spectra and SCDs from simulated maps.

Bayesian Simulation-based Inference for Cosmological Initial Conditions

Reconstructing astrophysical and cosmological fields from observations is challenging. It requires accounting for non-linear transformations, mixing of spatial structure, and noise. In contrast, forward simulators that map fields to observations are readily available for many applications. We present a versatile Bayesian field reconstruction algorithm rooted in simulation-based inference and enhanced by autoregressive modeling. The proposed technique is applicable to generic (non-differentiable) forward simulators and allows sampling from the posterior for the underlying field. We show first promising results on a proof-of-concept application: the recovery of cosmological initial conditions from late-time density fields.

Stochastic Super-resolution of Cosmological Simulations with Denoising Diffusion Models

In recent years, deep learning models have been successfully employed for augmenting low-resolution cosmological simulations with small-scale information, a task known as "super-resolution". So far, these cosmological super-resolution models have relied on generative adversarial networks (GANs), which can achieve highly realistic results, but suffer from various shortcomings (e.g. low sample diversity). We introduce denoising diffusion models as a powerful generative model for super-resolving cosmic large-scale structure predictions (as a first proof-of-concept in two dimensions). To obtain accurate results down to small scales, we develop a new "filter-boosted" training approach that redistributes the importance of different scales in the pixel-wise training objective. We demonstrate that our model not only produces convincing super-resolution images and power spectra consistent at the percent level, but is also able to reproduce the diversity of small-scale features consistent with a given low-resolution simulation. This enables uncertainty quantification for the generated small-scale features, which is critical for the usefulness of such super-resolution models as a viable surrogate model for cosmic structure formation.

Dim but not entirely dark: Extracting the Galactic Center Excess' source-count distribution with neural nets

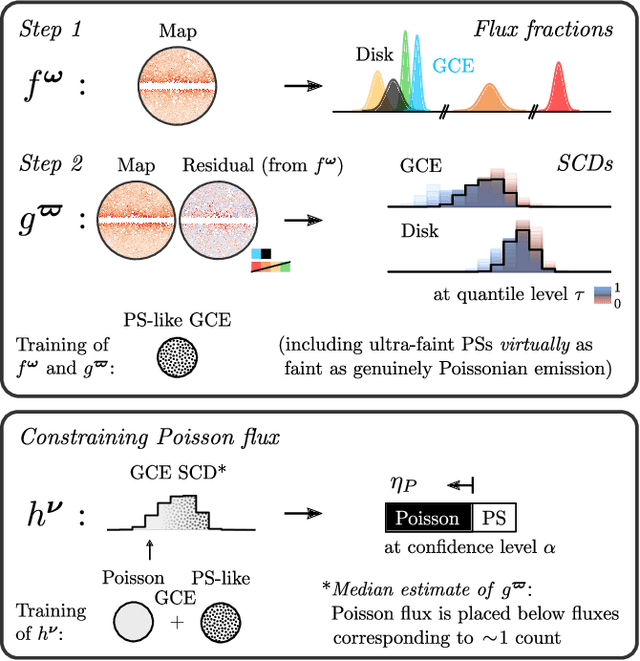
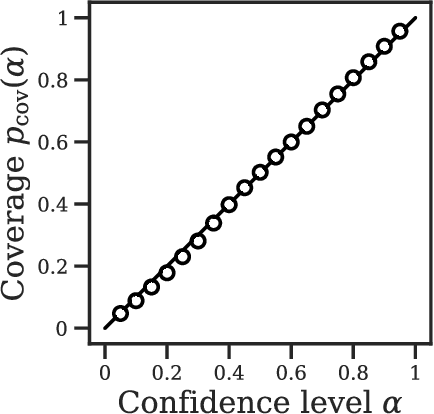
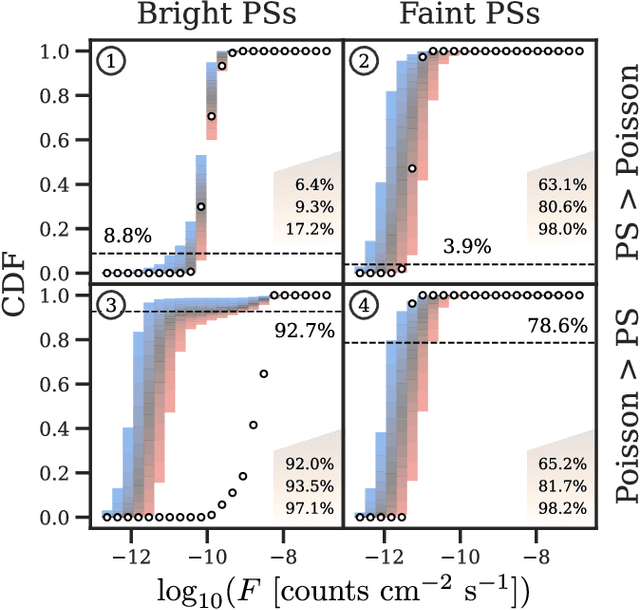
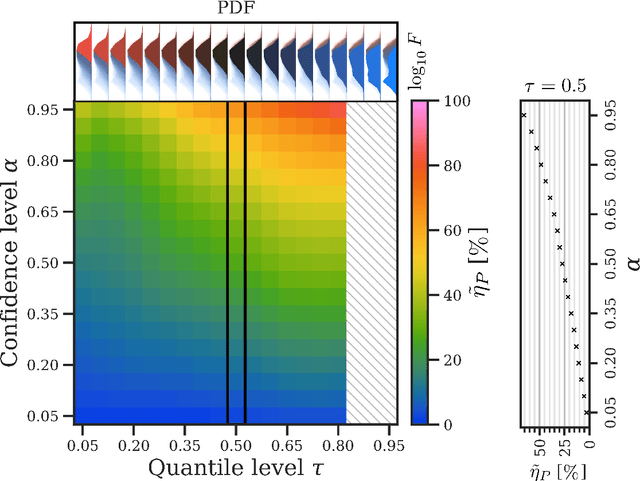
The two leading hypotheses for the Galactic Center Excess (GCE) in the $\textit{Fermi}$ data are an unresolved population of faint millisecond pulsars (MSPs) and dark-matter (DM) annihilation. The dichotomy between these explanations is typically reflected by modeling them as two separate emission components. However, point-sources (PSs) such as MSPs become statistically degenerate with smooth Poisson emission in the ultra-faint limit (formally where each source is expected to contribute much less than one photon on average), leading to an ambiguity that can render questions such as whether the emission is PS-like or Poissonian in nature ill-defined. We present a conceptually new approach that describes the PS and Poisson emission in a unified manner and only afterwards derives constraints on the Poissonian component from the so obtained results. For the implementation of this approach, we leverage deep learning techniques, centered around a neural network-based method for histogram regression that expresses uncertainties in terms of quantiles. We demonstrate that our method is robust against a number of systematics that have plagued previous approaches, in particular DM / PS misattribution. In the $\textit{Fermi}$ data, we find a faint GCE described by a median source-count distribution (SCD) peaked at a flux of $\sim4 \times 10^{-11} \ \text{counts} \ \text{cm}^{-2} \ \text{s}^{-1}$ (corresponding to $\sim3 - 4$ expected counts per PS), which would require $N \sim \mathcal{O}(10^4)$ sources to explain the entire excess (median value $N = \text{29,300}$ across the sky). Although faint, this SCD allows us to derive the constraint $\eta_P \leq 66\%$ for the Poissonian fraction of the GCE flux $\eta_P$ at 95% confidence, suggesting that a substantial amount of the GCE flux is due to PSs.

The Earth Mover's Pinball Loss: Quantiles for Histogram-Valued Regression

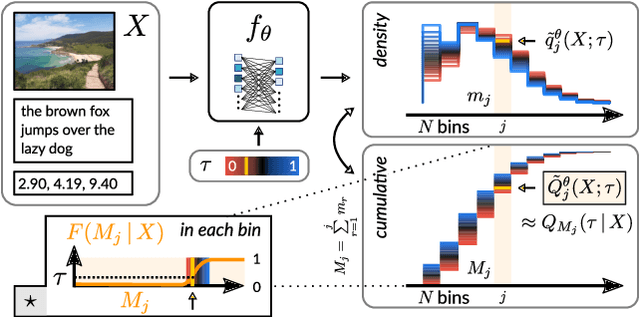
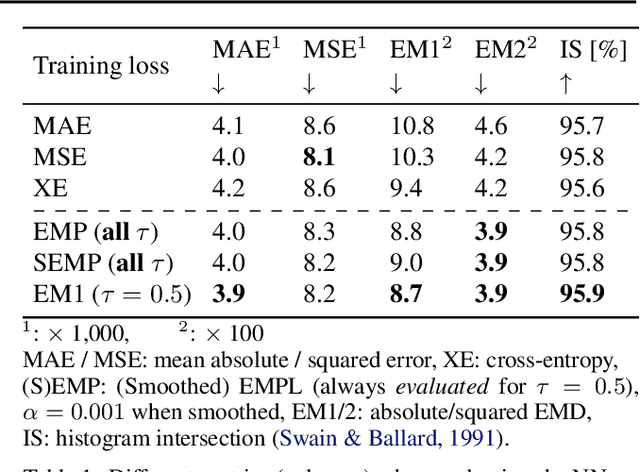
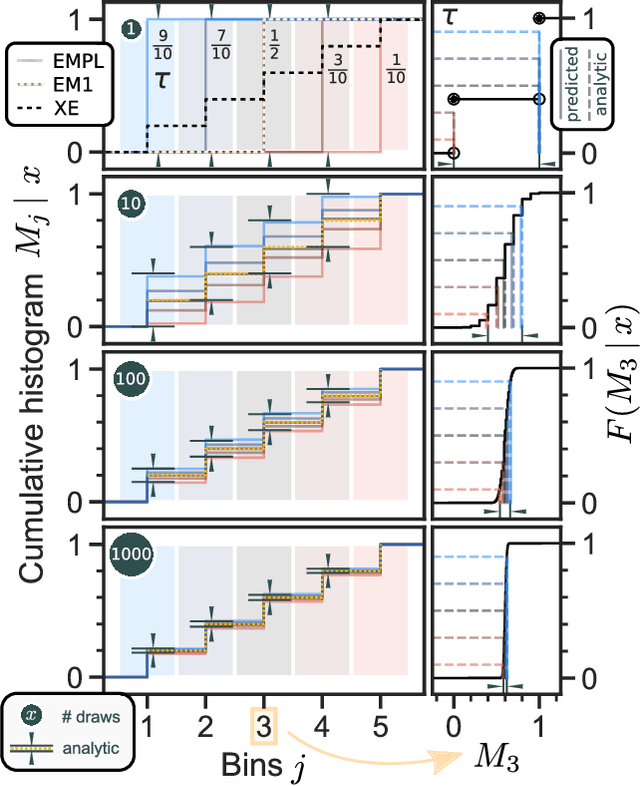
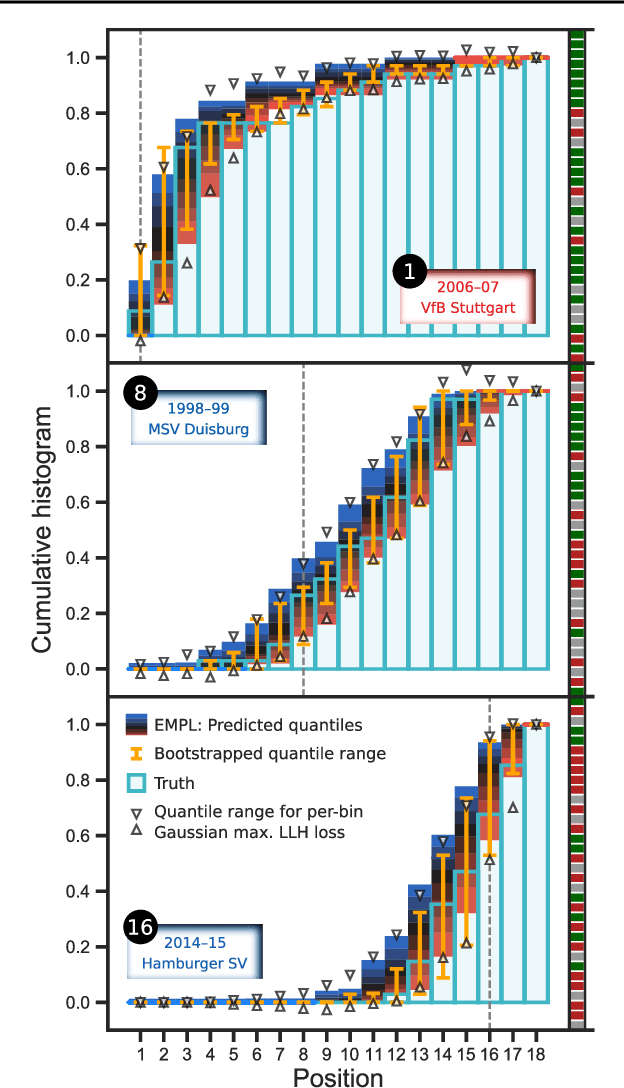
Although ubiquitous in the sciences, histogram data have not received much attention by the Deep Learning community. Whilst regression and classification tasks for scalar and vector data are routinely solved by neural networks, a principled approach for estimating histogram labels as a function of an input vector or image is lacking in the literature. We present a dedicated method for Deep Learning-based histogram regression, which incorporates cross-bin information and yields distributions over possible histograms, expressed by $\tau$-quantiles of the cumulative histogram in each bin. The crux of our approach is a new loss function obtained by applying the pinball loss to the cumulative histogram, which for 1D histograms reduces to the Earth Mover's distance (EMD) in the special case of the median ($\tau = 0.5$), and generalizes it to arbitrary quantiles. We validate our method with an illustrative toy example, a football-related task, and an astrophysical computer vision problem. We show that with our loss function, the accuracy of the predicted median histograms is very similar to the standard EMD case (and higher than for per-bin loss functions such as cross-entropy), while the predictions become much more informative at almost no additional computational cost.

The GCE in a New Light: Disentangling the $γ$-ray Sky with Bayesian Graph Convolutional Neural Networks

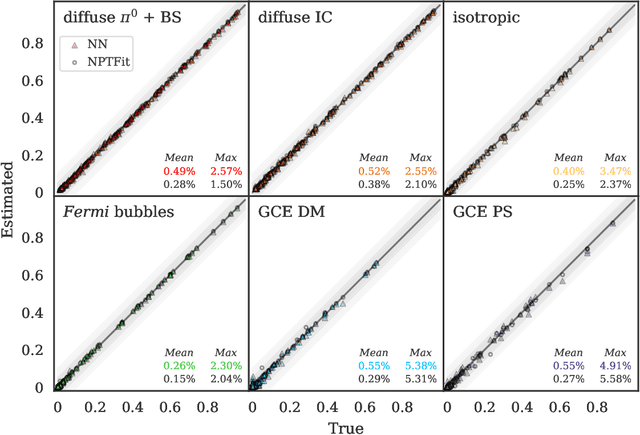
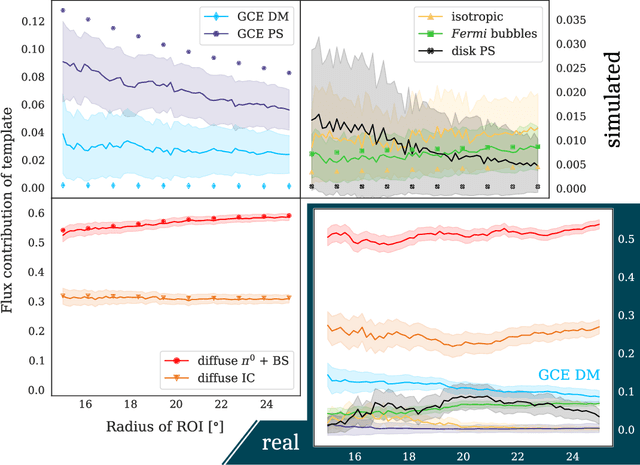
A fundamental question regarding the Galactic Center Excess (GCE) is whether the underlying structure is point-like or smooth. This debate, often framed in terms of a millisecond pulsar or annihilating dark matter (DM) origin for the emission, awaits a conclusive resolution. In this work we weigh in on the problem using Bayesian graph convolutional neural networks. In simulated data, our neural network (NN) is able to reconstruct the flux of inner galaxy emission components to on average $\sim$0.5%, comparable to the non-Poissonian template fit (NPTF). When applied to the actual $\textit{Fermi}$-LAT data, we find that the NN estimates for the flux fractions from the background templates are consistent with the NPTF; however, the GCE is almost entirely attributed to smooth emission. While suggestive, we do not claim a definitive resolution for the GCE, as the NN tends to underestimate the flux of point-sources peaked near the 1$\sigma$ detection threshold. Yet the technique displays robustness to a number of systematics, including reconstructing injected DM, diffuse mismodeling, and unmodeled north-south asymmetries. So while the NN is hinting at a smooth origin for the GCE at present, with further refinements we argue that Bayesian Deep Learning is well placed to resolve this DM mystery.

A unified framework for 21cm tomography sample generation and parameter inference with Progressively Growing GANs

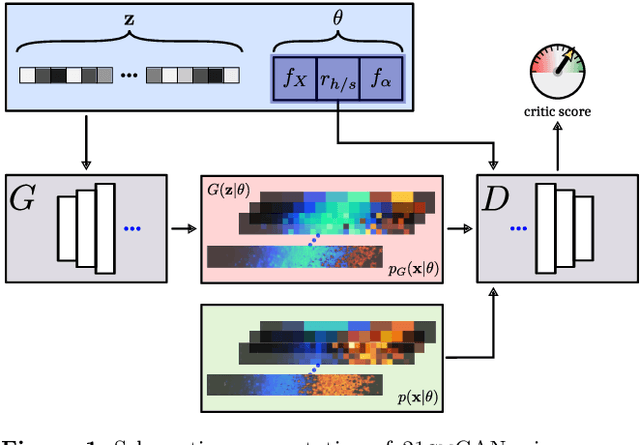
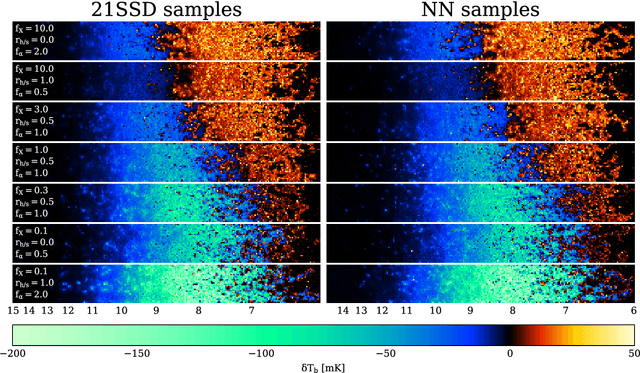
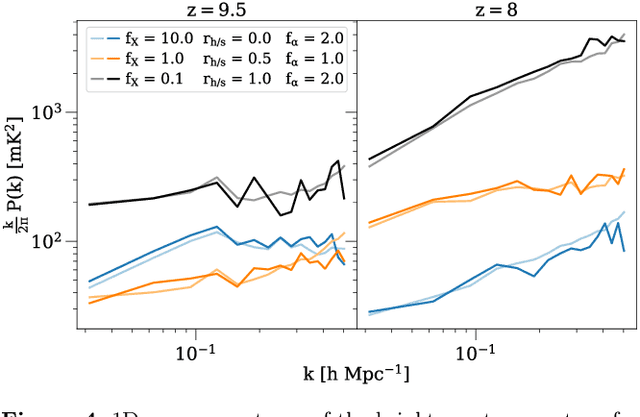
Creating a database of 21cm brightness temperature signals from the Epoch of Reionisation (EoR) for an array of reionisation histories is a complex and computationally expensive task, given the range of astrophysical processes involved and the possibly high-dimensional parameter space that is to be probed. We utilise a specific type of neural network, a Progressively Growing Generative Adversarial Network (PGGAN), to produce realistic tomography images of the 21cm brightness temperature during the EoR, covering a continuous three-dimensional parameter space that models varying X-ray emissivity, Lyman band emissivity, and ratio between hard and soft X-rays. The GPU-trained network generates new samples at a resolution of $\sim 3'$ in a second (on a laptop CPU), and the resulting global 21cm signal, power spectrum, and pixel distribution function agree well with those of the training data, taken from the 21SSD catalogue \citep{Semelin2017}. Finally, we showcase how a trained PGGAN can be leveraged for the converse task of inferring parameters from 21cm tomography samples via Approximate Bayesian Computation.