A deep learning framework for jointly extracting spectra and source-count distributions in astronomy

Astronomical observations typically provide three-dimensional maps, encoding the distribution of the observed flux in (1) the two angles of the celestial sphere and (2) energy/frequency. An important task regarding such maps is to statistically characterize populations of point sources too dim to be individually detected. As the properties of a single dim source will be poorly constrained, instead one commonly studies the population as a whole, inferring a source-count distribution (SCD) that describes the number density of sources as a function of their brightness. Statistical and machine learning methods for recovering SCDs exist; however, they typically entirely neglect spectral information associated with the energy distribution of the flux. We present a deep learning framework able to jointly reconstruct the spectra of different emission components and the SCD of point-source populations. In a proof-of-concept example, we show that our method accurately extracts even complex-shaped spectra and SCDs from simulated maps.

Dim but not entirely dark: Extracting the Galactic Center Excess' source-count distribution with neural nets

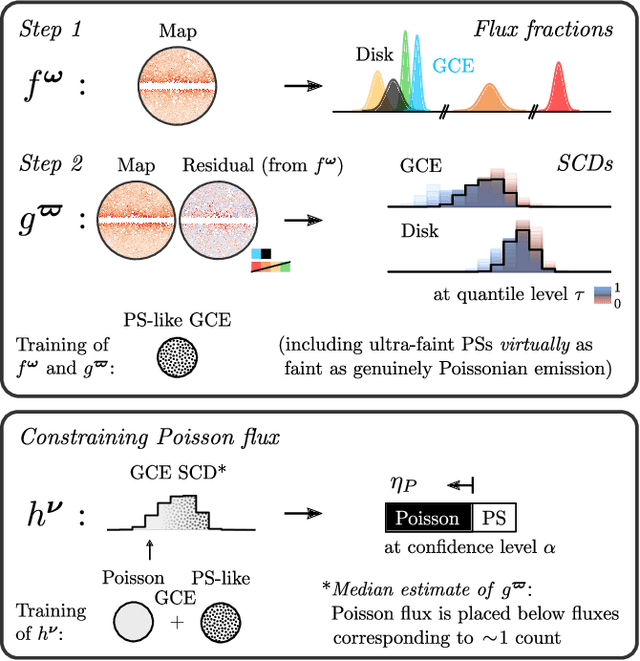
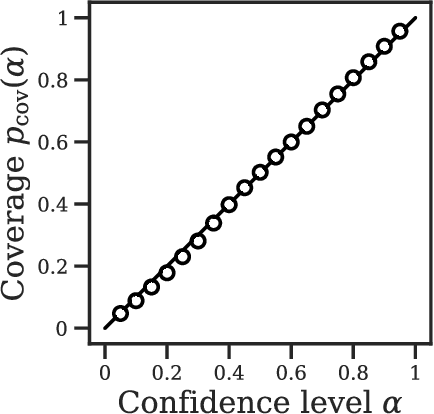
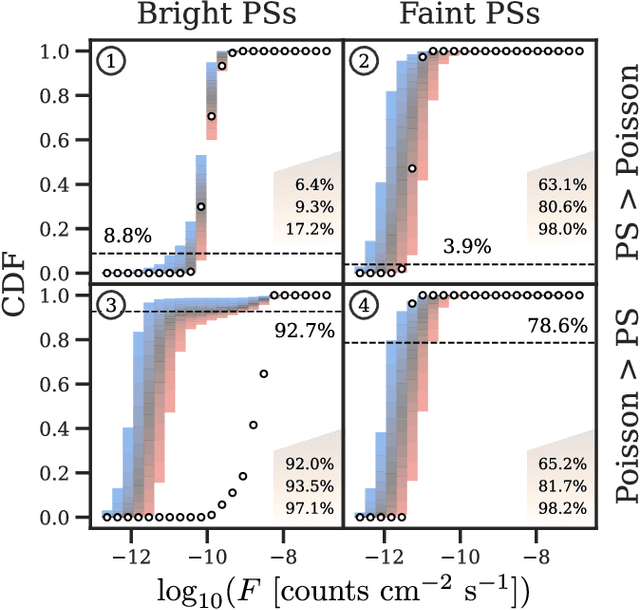
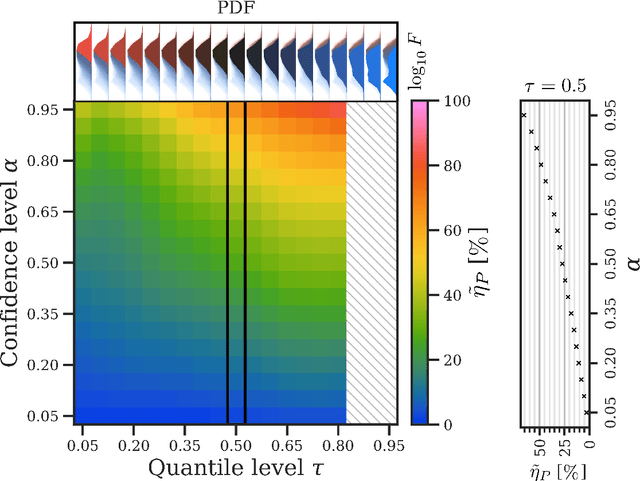
The two leading hypotheses for the Galactic Center Excess (GCE) in the $\textit{Fermi}$ data are an unresolved population of faint millisecond pulsars (MSPs) and dark-matter (DM) annihilation. The dichotomy between these explanations is typically reflected by modeling them as two separate emission components. However, point-sources (PSs) such as MSPs become statistically degenerate with smooth Poisson emission in the ultra-faint limit (formally where each source is expected to contribute much less than one photon on average), leading to an ambiguity that can render questions such as whether the emission is PS-like or Poissonian in nature ill-defined. We present a conceptually new approach that describes the PS and Poisson emission in a unified manner and only afterwards derives constraints on the Poissonian component from the so obtained results. For the implementation of this approach, we leverage deep learning techniques, centered around a neural network-based method for histogram regression that expresses uncertainties in terms of quantiles. We demonstrate that our method is robust against a number of systematics that have plagued previous approaches, in particular DM / PS misattribution. In the $\textit{Fermi}$ data, we find a faint GCE described by a median source-count distribution (SCD) peaked at a flux of $\sim4 \times 10^{-11} \ \text{counts} \ \text{cm}^{-2} \ \text{s}^{-1}$ (corresponding to $\sim3 - 4$ expected counts per PS), which would require $N \sim \mathcal{O}(10^4)$ sources to explain the entire excess (median value $N = \text{29,300}$ across the sky). Although faint, this SCD allows us to derive the constraint $\eta_P \leq 66\%$ for the Poissonian fraction of the GCE flux $\eta_P$ at 95% confidence, suggesting that a substantial amount of the GCE flux is due to PSs.

The GCE in a New Light: Disentangling the $γ$-ray Sky with Bayesian Graph Convolutional Neural Networks

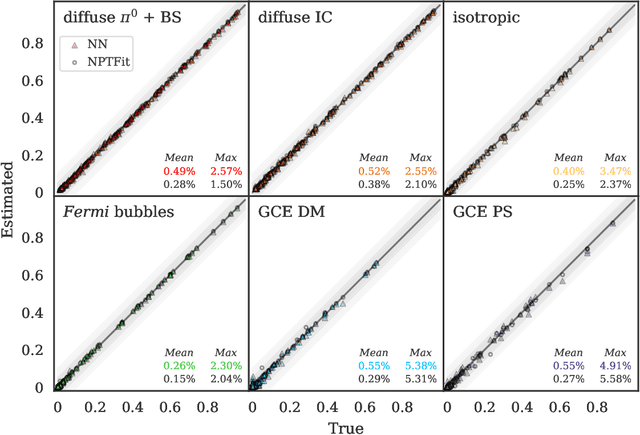
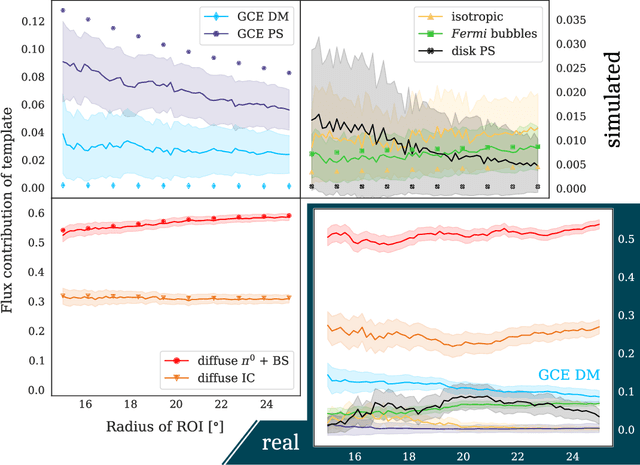
A fundamental question regarding the Galactic Center Excess (GCE) is whether the underlying structure is point-like or smooth. This debate, often framed in terms of a millisecond pulsar or annihilating dark matter (DM) origin for the emission, awaits a conclusive resolution. In this work we weigh in on the problem using Bayesian graph convolutional neural networks. In simulated data, our neural network (NN) is able to reconstruct the flux of inner galaxy emission components to on average $\sim$0.5%, comparable to the non-Poissonian template fit (NPTF). When applied to the actual $\textit{Fermi}$-LAT data, we find that the NN estimates for the flux fractions from the background templates are consistent with the NPTF; however, the GCE is almost entirely attributed to smooth emission. While suggestive, we do not claim a definitive resolution for the GCE, as the NN tends to underestimate the flux of point-sources peaked near the 1$\sigma$ detection threshold. Yet the technique displays robustness to a number of systematics, including reconstructing injected DM, diffuse mismodeling, and unmodeled north-south asymmetries. So while the NN is hinting at a smooth origin for the GCE at present, with further refinements we argue that Bayesian Deep Learning is well placed to resolve this DM mystery.