Dim but not entirely dark: Extracting the Galactic Center Excess' source-count distribution with neural nets
Paper and Code
Jul 19, 2021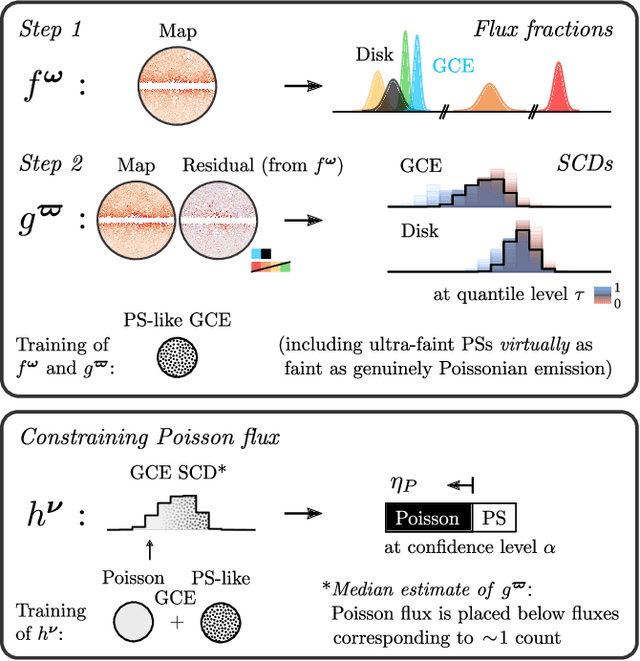
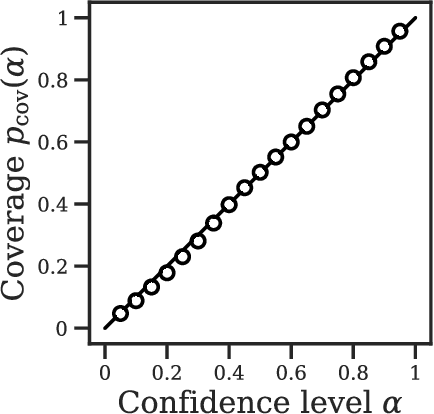
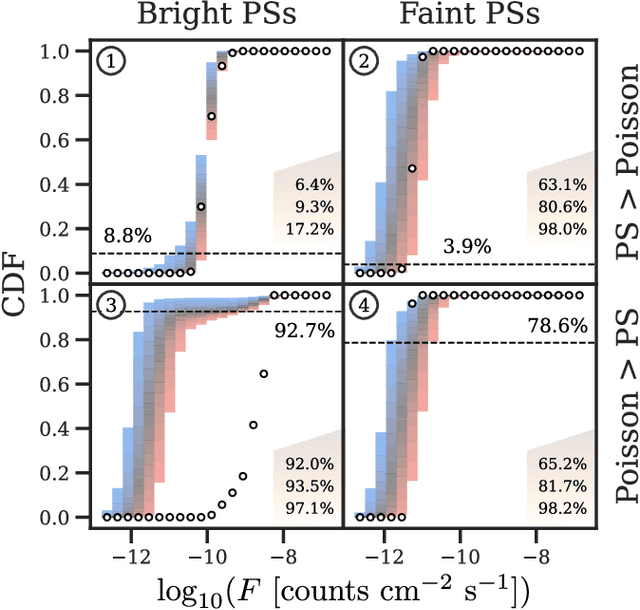
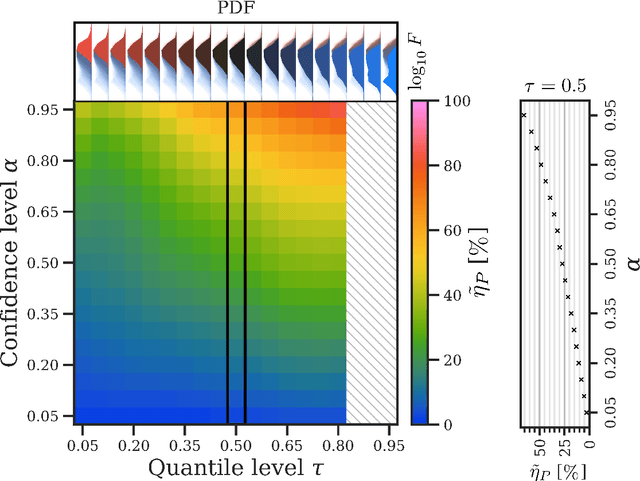
The two leading hypotheses for the Galactic Center Excess (GCE) in the $\textit{Fermi}$ data are an unresolved population of faint millisecond pulsars (MSPs) and dark-matter (DM) annihilation. The dichotomy between these explanations is typically reflected by modeling them as two separate emission components. However, point-sources (PSs) such as MSPs become statistically degenerate with smooth Poisson emission in the ultra-faint limit (formally where each source is expected to contribute much less than one photon on average), leading to an ambiguity that can render questions such as whether the emission is PS-like or Poissonian in nature ill-defined. We present a conceptually new approach that describes the PS and Poisson emission in a unified manner and only afterwards derives constraints on the Poissonian component from the so obtained results. For the implementation of this approach, we leverage deep learning techniques, centered around a neural network-based method for histogram regression that expresses uncertainties in terms of quantiles. We demonstrate that our method is robust against a number of systematics that have plagued previous approaches, in particular DM / PS misattribution. In the $\textit{Fermi}$ data, we find a faint GCE described by a median source-count distribution (SCD) peaked at a flux of $\sim4 \times 10^{-11} \ \text{counts} \ \text{cm}^{-2} \ \text{s}^{-1}$ (corresponding to $\sim3 - 4$ expected counts per PS), which would require $N \sim \mathcal{O}(10^4)$ sources to explain the entire excess (median value $N = \text{29,300}$ across the sky). Although faint, this SCD allows us to derive the constraint $\eta_P \leq 66\%$ for the Poissonian fraction of the GCE flux $\eta_P$ at 95% confidence, suggesting that a substantial amount of the GCE flux is due to PSs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge