Low-Budget Simulation-Based Inference with Bayesian Neural Networks

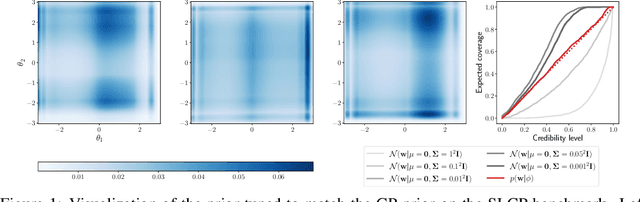
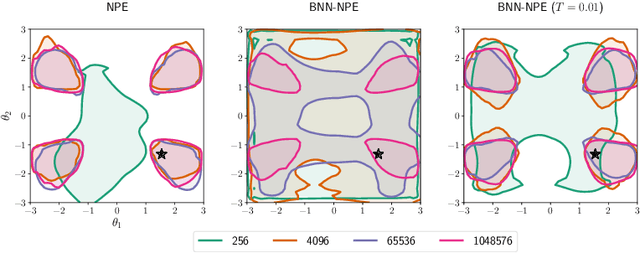
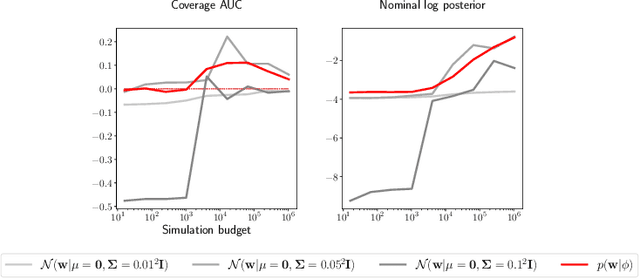
Simulation-based inference methods have been shown to be inaccurate in the data-poor regime, when training simulations are limited or expensive. Under these circumstances, the inference network is particularly prone to overfitting, and using it without accounting for the computational uncertainty arising from the lack of identifiability of the network weights can lead to unreliable results. To address this issue, we propose using Bayesian neural networks in low-budget simulation-based inference, thereby explicitly accounting for the computational uncertainty of the posterior approximation. We design a family of Bayesian neural network priors that are tailored for inference and show that they lead to well-calibrated posteriors on tested benchmarks, even when as few as $O(10)$ simulations are available. This opens up the possibility of performing reliable simulation-based inference using very expensive simulators, as we demonstrate on a problem from the field of cosmology where single simulations are computationally expensive. We show that Bayesian neural networks produce informative and well-calibrated posterior estimates with only a few hundred simulations.

Calibrating Neural Simulation-Based Inference with Differentiable Coverage Probability

Bayesian inference allows expressing the uncertainty of posterior belief under a probabilistic model given prior information and the likelihood of the evidence. Predominantly, the likelihood function is only implicitly established by a simulator posing the need for simulation-based inference (SBI). However, the existing algorithms can yield overconfident posteriors (Hermans *et al.*, 2022) defeating the whole purpose of credibility if the uncertainty quantification is inaccurate. We propose to include a calibration term directly into the training objective of the neural model in selected amortized SBI techniques. By introducing a relaxation of the classical formulation of calibration error we enable end-to-end backpropagation. The proposed method is not tied to any particular neural model and brings moderate computational overhead compared to the profits it introduces. It is directly applicable to existing computational pipelines allowing reliable black-box posterior inference. We empirically show on six benchmark problems that the proposed method achieves competitive or better results in terms of coverage and expected posterior density than the previously existing approaches.

Balancing Simulation-based Inference for Conservative Posteriors

Conservative inference is a major concern in simulation-based inference. It has been shown that commonly used algorithms can produce overconfident posterior approximations. Balancing has empirically proven to be an effective way to mitigate this issue. However, its application remains limited to neural ratio estimation. In this work, we extend balancing to any algorithm that provides a posterior density. In particular, we introduce a balanced version of both neural posterior estimation and contrastive neural ratio estimation. We show empirically that the balanced versions tend to produce conservative posterior approximations on a wide variety of benchmarks. In addition, we provide an alternative interpretation of the balancing condition in terms of the $\chi^2$ divergence.

Towards Reliable Simulation-Based Inference with Balanced Neural Ratio Estimation

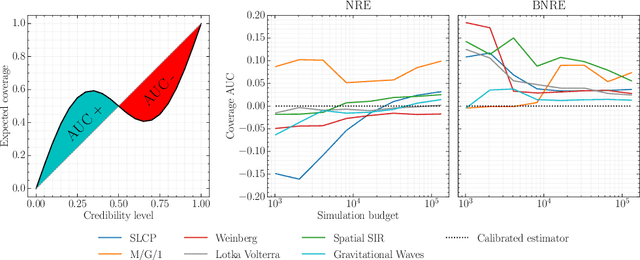
Modern approaches for simulation-based inference rely upon deep learning surrogates to enable approximate inference with computer simulators. In practice, the estimated posteriors' computational faithfulness is, however, rarely guaranteed. For example, Hermans et al. (2021) show that current simulation-based inference algorithms can produce posteriors that are overconfident, hence risking false inferences. In this work, we introduce Balanced Neural Ratio Estimation (BNRE), a variation of the NRE algorithm designed to produce posterior approximations that tend to be more conservative, hence improving their reliability, while sharing the same Bayes optimal solution. We achieve this by enforcing a balancing condition that increases the quantified uncertainty in small simulation budget regimes while still converging to the exact posterior as the budget increases. We provide theoretical arguments showing that BNRE tends to produce posterior surrogates that are more conservative than NRE's. We evaluate BNRE on a wide variety of tasks and show that it produces conservative posterior surrogates on all tested benchmarks and simulation budgets. Finally, we emphasize that BNRE is straightforward to implement over NRE and does not introduce any computational overhead.

SAE: Sequential Anchored Ensembles

Computing the Bayesian posterior of a neural network is a challenging task due to the high-dimensionality of the parameter space. Anchored ensembles approximate the posterior by training an ensemble of neural networks on anchored losses designed for the optima to follow the Bayesian posterior. Training an ensemble, however, becomes computationally expensive as its number of members grows since the full training procedure is repeated for each member. In this note, we present Sequential Anchored Ensembles (SAE), a lightweight alternative to anchored ensembles. Instead of training each member of the ensemble from scratch, the members are trained sequentially on losses sampled with high auto-correlation, hence enabling fast convergence of the neural networks and efficient approximation of the Bayesian posterior. SAE outperform anchored ensembles, for a given computational budget, on some benchmarks while showing comparable performance on the others and achieved 2nd and 3rd place in the light and extended tracks of the NeurIPS 2021 Approximate Inference in Bayesian Deep Learning competition.

Averting A Crisis In Simulation-Based Inference

We present extensive empirical evidence showing that current Bayesian simulation-based inference algorithms are inadequate for the falsificationist methodology of scientific inquiry. Our results collected through months of experimental computations show that all benchmarked algorithms -- (S)NPE, (S)NRE, SNL and variants of ABC -- may produce overconfident posterior approximations, which makes them demonstrably unreliable and dangerous if one's scientific goal is to constrain parameters of interest. We believe that failing to address this issue will lead to a well-founded trust crisis in simulation-based inference. For this reason, we argue that research efforts should now consider theoretical and methodological developments of conservative approximate inference algorithms and present research directions towards this objective. In this regard, we show empirical evidence that ensembles are consistently more reliable.

Lightning-Fast Gravitational Wave Parameter Inference through Neural Amortization

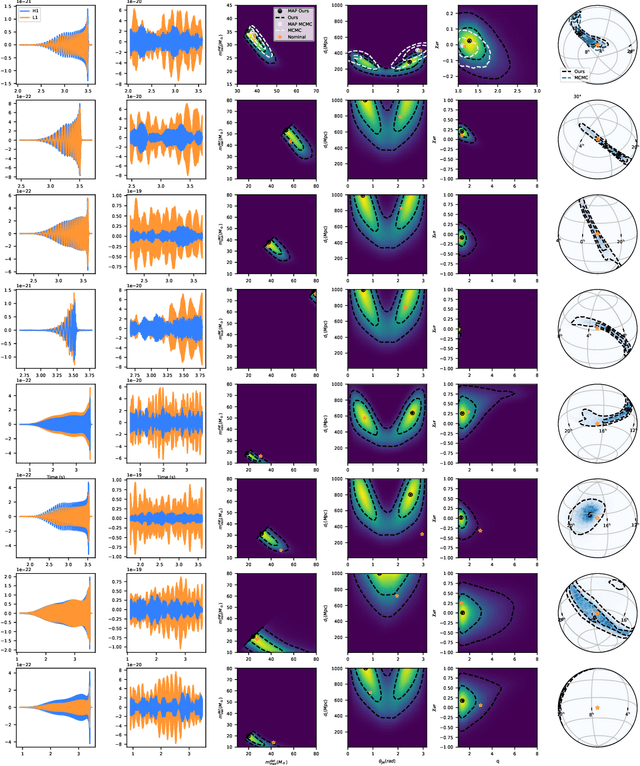
Gravitational waves from compact binaries measured by the LIGO and Virgo detectors are routinely analyzed using Markov Chain Monte Carlo sampling algorithms. Because the evaluation of the likelihood function requires evaluating millions of waveform models that link between signal shapes and the source parameters, running Markov chains until convergence is typically expensive and requires days of computation. In this extended abstract, we provide a proof of concept that demonstrates how the latest advances in neural simulation-based inference can speed up the inference time by up to three orders of magnitude -- from days to minutes -- without impairing the performance. Our approach is based on a convolutional neural network modeling the likelihood-to-evidence ratio and entirely amortizes the computation of the posterior. We find that our model correctly estimates credible intervals for the parameters of simulated gravitational waves.