Differentiable Molecular Simulations for Control and Learning
Paper and Code
Feb 27, 2020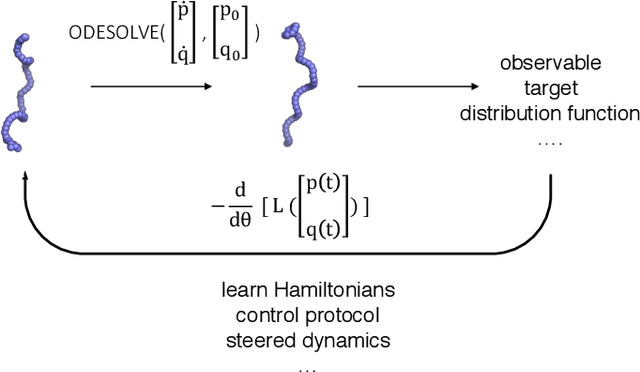
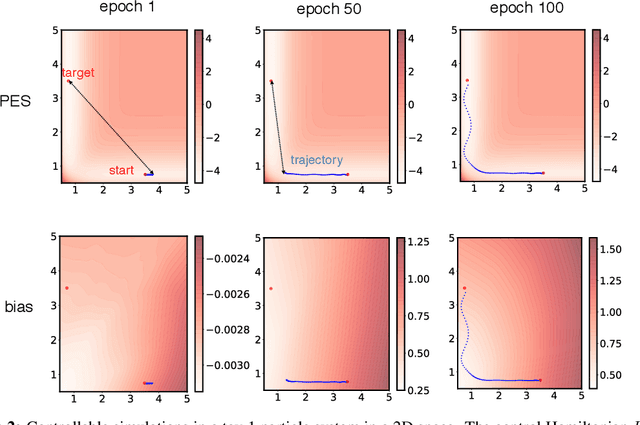
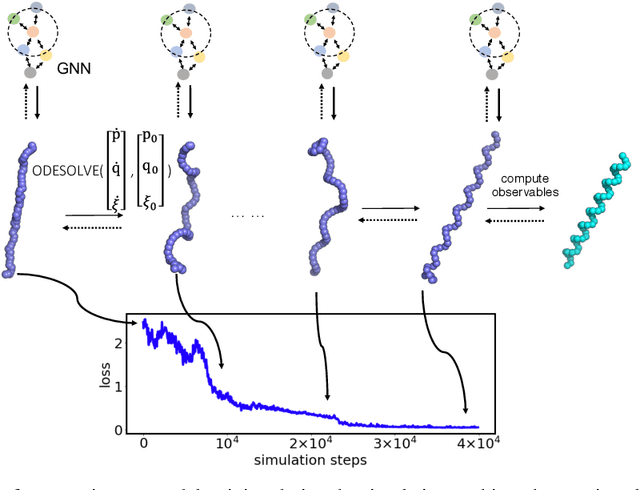
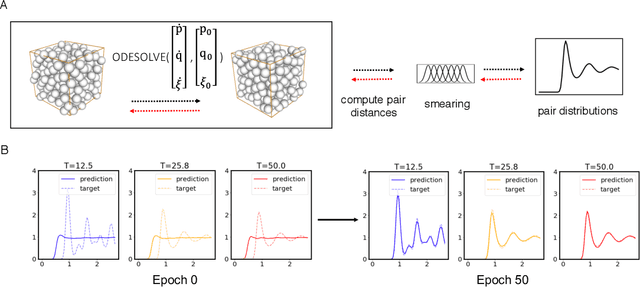
Molecular dynamics simulations use statistical mechanics at the atomistic scale to enable both the elucidation of fundamental mechanisms and the engineering of matter for desired tasks. The behavior of molecular systems at the microscale is typically simulated with differential equations parameterized by a Hamiltonian, or energy function. The Hamiltonian describes the state of the system and its interactions with the environment. In order to derive predictive microscopic models, one wishes to infer a molecular Hamiltonian that agrees with observed macroscopic quantities. From the perspective of engineering, one wishes to control the Hamiltonian to achieve desired simulation outcomes and structures, as in self-assembly and optical control, to then realize systems with the desired Hamiltonian in the lab. In both cases, the goal is to modify the Hamiltonian such that emergent properties of the simulated system match a given target. We demonstrate how this can be achieved using differentiable simulations where bulk target observables and simulation outcomes can be analytically differentiated with respect to Hamiltonians, opening up new routes for parameterizing Hamiltonians to infer macroscopic models and develop control protocols.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge