The Well: a Large-Scale Collection of Diverse Physics Simulations for Machine Learning

Machine learning based surrogate models offer researchers powerful tools for accelerating simulation-based workflows. However, as standard datasets in this space often cover small classes of physical behavior, it can be difficult to evaluate the efficacy of new approaches. To address this gap, we introduce the Well: a large-scale collection of datasets containing numerical simulations of a wide variety of spatiotemporal physical systems. The Well draws from domain experts and numerical software developers to provide 15TB of data across 16 datasets covering diverse domains such as biological systems, fluid dynamics, acoustic scattering, as well as magneto-hydrodynamic simulations of extra-galactic fluids or supernova explosions. These datasets can be used individually or as part of a broader benchmark suite. To facilitate usage of the Well, we provide a unified PyTorch interface for training and evaluating models. We demonstrate the function of this library by introducing example baselines that highlight the new challenges posed by the complex dynamics of the Well. The code and data is available at https://github.com/PolymathicAI/the_well.

Learned Coarse Models for Efficient Turbulence Simulation

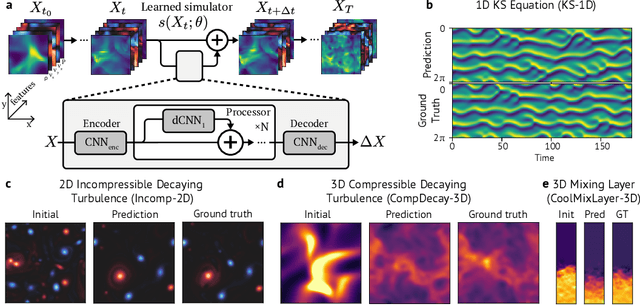
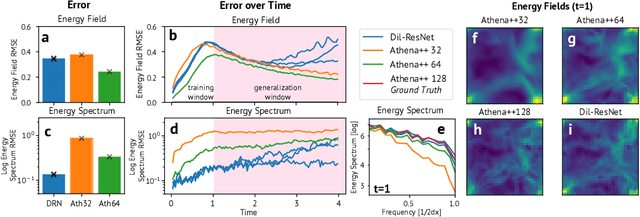
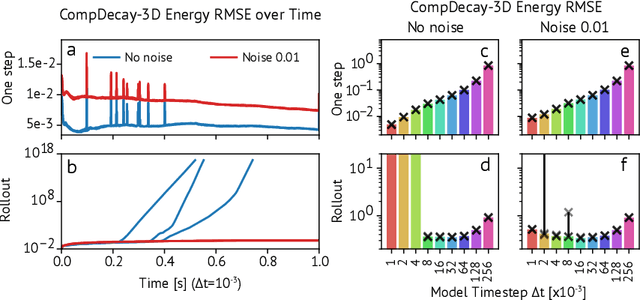
Turbulence simulation with classical numerical solvers requires very high-resolution grids to accurately resolve dynamics. Here we train learned simulators at low spatial and temporal resolutions to capture turbulent dynamics generated at high resolution. We show that our proposed model can simulate turbulent dynamics more accurately than classical numerical solvers at the same low resolutions across various scientifically relevant metrics. Our model is trained end-to-end from data and is capable of learning a range of challenging chaotic and turbulent dynamics at low resolution, including trajectories generated by the state-of-the-art Athena++ engine. We show that our simpler, general-purpose architecture outperforms various more specialized, turbulence-specific architectures from the learned turbulence simulation literature. In general, we see that learned simulators yield unstable trajectories; however, we show that tuning training noise and temporal downsampling solves this problem. We also find that while generalization beyond the training distribution is a challenge for learned models, training noise, convolutional architectures, and added loss constraints can help. Broadly, we conclude that our learned simulator outperforms traditional solvers run on coarser grids, and emphasize that simple design choices can offer stability and robust generalization.