Rudy Morel
Test-time Generalization for Physics through Neural Operator Splitting
Jan 31, 2026Abstract:Neural operators have shown promise in learning solution maps of partial differential equations (PDEs), but they often struggle to generalize when test inputs lie outside the training distribution, such as novel initial conditions, unseen PDE coefficients or unseen physics. Prior works address this limitation with large-scale multiple physics pretraining followed by fine-tuning, but this still requires examples from the new dynamics, falling short of true zero-shot generalization. In this work, we propose a method to enhance generalization at test time, i.e., without modifying pretrained weights. Building on DISCO, which provides a dictionary of neural operators trained across different dynamics, we introduce a neural operator splitting strategy that, at test time, searches over compositions of training operators to approximate unseen dynamics. On challenging out-of-distribution tasks including parameter extrapolation and novel combinations of physics phenomena, our approach achieves state-of-the-art zero-shot generalization results, while being able to recover the underlying PDE parameters. These results underscore test-time computation as a key avenue for building flexible, compositional, and generalizable neural operators.
Walrus: A Cross-Domain Foundation Model for Continuum Dynamics
Nov 19, 2025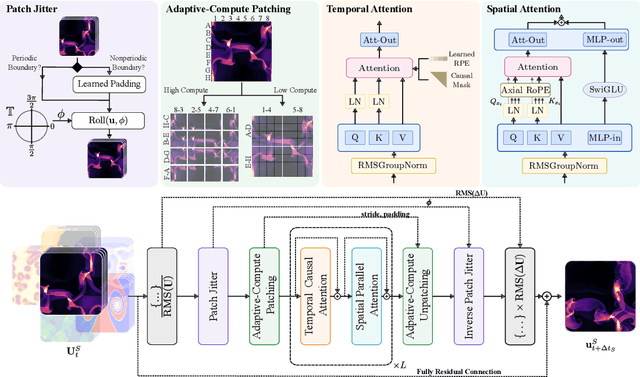


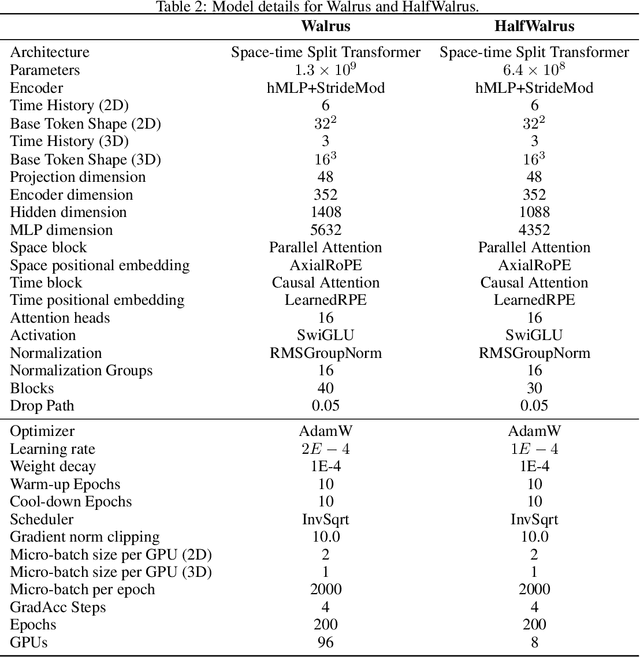
Abstract:Foundation models have transformed machine learning for language and vision, but achieving comparable impact in physical simulation remains a challenge. Data heterogeneity and unstable long-term dynamics inhibit learning from sufficiently diverse dynamics, while varying resolutions and dimensionalities challenge efficient training on modern hardware. Through empirical and theoretical analysis, we incorporate new approaches to mitigate these obstacles, including a harmonic-analysis-based stabilization method, load-balanced distributed 2D and 3D training strategies, and compute-adaptive tokenization. Using these tools, we develop Walrus, a transformer-based foundation model developed primarily for fluid-like continuum dynamics. Walrus is pretrained on nineteen diverse scenarios spanning astrophysics, geoscience, rheology, plasma physics, acoustics, and classical fluids. Experiments show that Walrus outperforms prior foundation models on both short and long term prediction horizons on downstream tasks and across the breadth of pretraining data, while ablation studies confirm the value of our contributions to forecast stability, training throughput, and transfer performance over conventional approaches. Code and weights are released for community use.
DISCO: learning to DISCover an evolution Operator for multi-physics-agnostic prediction
Apr 28, 2025Abstract:We address the problem of predicting the next state of a dynamical system governed by unknown temporal partial differential equations (PDEs) using only a short trajectory. While standard transformers provide a natural black-box solution to this task, the presence of a well-structured evolution operator in the data suggests a more tailored and efficient approach. Specifically, when the PDE is fully known, classical numerical solvers can evolve the state accurately with only a few parameters. Building on this observation, we introduce DISCO, a model that uses a large hypernetwork to process a short trajectory and generate the parameters of a much smaller operator network, which then predicts the next state through time integration. Our framework decouples dynamics estimation (i.e., DISCovering an evolution operator from a short trajectory) from state prediction (i.e., evolving this operator). Experiments show that pretraining our model on diverse physics datasets achieves state-of-the-art performance while requiring significantly fewer epochs. Moreover, it generalizes well and remains competitive when fine-tuned on downstream tasks.
The Well: a Large-Scale Collection of Diverse Physics Simulations for Machine Learning
Nov 30, 2024



Abstract:Machine learning based surrogate models offer researchers powerful tools for accelerating simulation-based workflows. However, as standard datasets in this space often cover small classes of physical behavior, it can be difficult to evaluate the efficacy of new approaches. To address this gap, we introduce the Well: a large-scale collection of datasets containing numerical simulations of a wide variety of spatiotemporal physical systems. The Well draws from domain experts and numerical software developers to provide 15TB of data across 16 datasets covering diverse domains such as biological systems, fluid dynamics, acoustic scattering, as well as magneto-hydrodynamic simulations of extra-galactic fluids or supernova explosions. These datasets can be used individually or as part of a broader benchmark suite. To facilitate usage of the Well, we provide a unified PyTorch interface for training and evaluating models. We demonstrate the function of this library by introducing example baselines that highlight the new challenges posed by the complex dynamics of the Well. The code and data is available at https://github.com/PolymathicAI/the_well.
Contextual Counting: A Mechanistic Study of Transformers on a Quantitative Task
May 30, 2024Abstract:Transformers have revolutionized machine learning across diverse domains, yet understanding their behavior remains crucial, particularly in high-stakes applications. This paper introduces the contextual counting task, a novel toy problem aimed at enhancing our understanding of Transformers in quantitative and scientific contexts. This task requires precise localization and computation within datasets, akin to object detection or region-based scientific analysis. We present theoretical and empirical analysis using both causal and non-causal Transformer architectures, investigating the influence of various positional encodings on performance and interpretability. In particular, we find that causal attention is much better suited for the task, and that no positional embeddings lead to the best accuracy, though rotary embeddings are competitive and easier to train. We also show that out of distribution performance is tightly linked to which tokens it uses as a bias term.
Scattering Spectra Models for Physics
Jun 29, 2023Abstract:Physicists routinely need probabilistic models for a number of tasks such as parameter inference or the generation of new realizations of a field. Establishing such models for highly non-Gaussian fields is a challenge, especially when the number of samples is limited. In this paper, we introduce scattering spectra models for stationary fields and we show that they provide accurate and robust statistical descriptions of a wide range of fields encountered in physics. These models are based on covariances of scattering coefficients, i.e. wavelet decomposition of a field coupled with a point-wise modulus. After introducing useful dimension reductions taking advantage of the regularity of a field under rotation and scaling, we validate these models on various multi-scale physical fields and demonstrate that they reproduce standard statistics, including spatial moments up to 4th order. These scattering spectra provide us with a low-dimensional structured representation that captures key properties encountered in a wide range of physical fields. These generic models can be used for data exploration, classification, parameter inference, symmetry detection, and component separation.
Martian time-series unraveled: A multi-scale nested approach with factorial variational autoencoders
May 25, 2023Abstract:Unsupervised source separation involves unraveling an unknown set of source signals recorded through a mixing operator, with limited prior knowledge about the sources, and only access to a dataset of signal mixtures. This problem is inherently ill-posed and is further challenged by the variety of time-scales exhibited by sources in time series data. Existing methods typically rely on a preselected window size that limits their capacity to handle multi-scale sources. To address this issue, instead of operating in the time domain, we propose an unsupervised multi-scale clustering and source separation framework by leveraging wavelet scattering covariances that provide a low-dimensional representation of stochastic processes, capable of distinguishing between different non-Gaussian stochastic processes. Nested within this representation space, we develop a factorial Gaussian-mixture variational autoencoder that is trained to (1) probabilistically cluster sources at different time-scales and (2) independently sample scattering covariance representations associated with each cluster. Using samples from each cluster as prior information, we formulate source separation as an optimization problem in the wavelet scattering covariance representation space, resulting in separated sources in the time domain. When applied to seismic data recorded during the NASA InSight mission on Mars, our multi-scale nested approach proves to be a powerful tool for discriminating between sources varying greatly in time-scale, e.g., minute-long transient one-sided pulses (known as ``glitches'') and structured ambient noises resulting from atmospheric activities that typically last for tens of minutes. These results provide an opportunity to conduct further investigations into the isolated sources related to atmospheric-surface interactions, thermal relaxations, and other complex phenomena.
Unearthing InSights into Mars: unsupervised source separation with limited data
Jan 27, 2023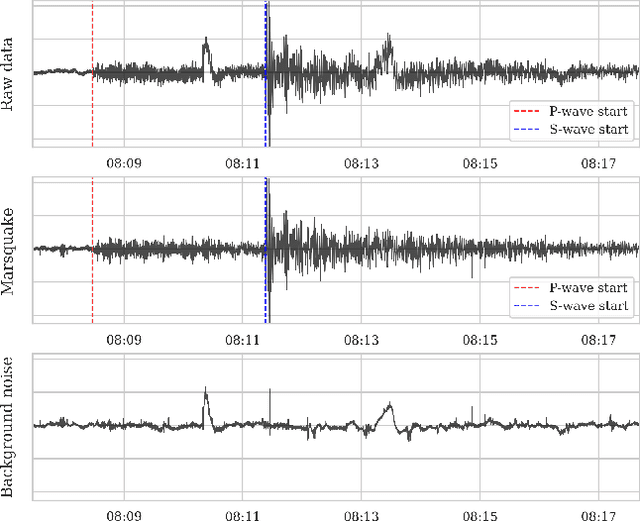
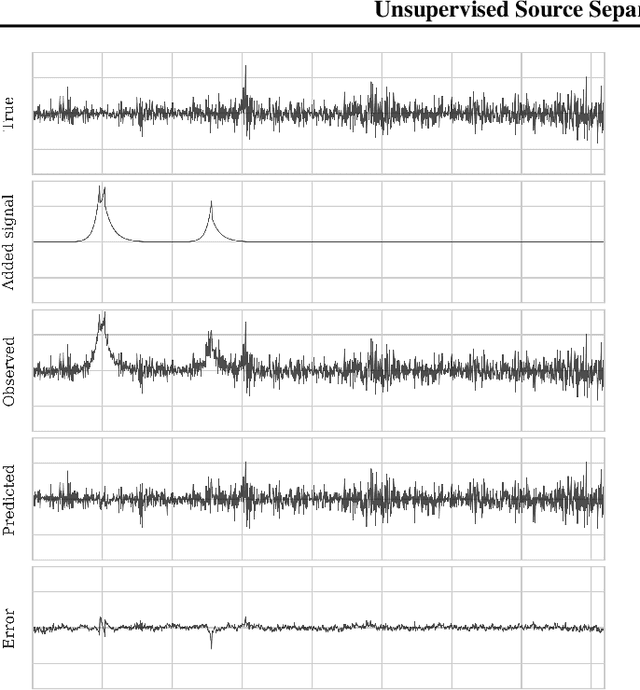
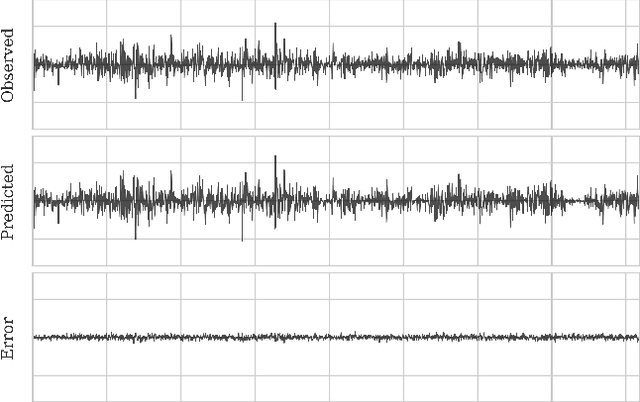
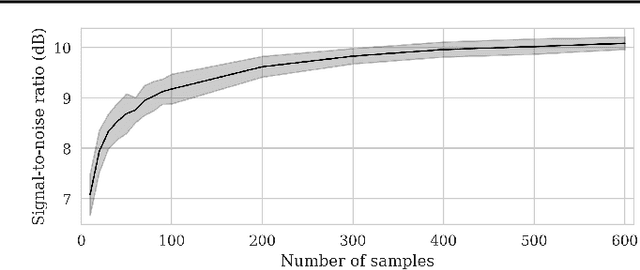
Abstract:Source separation entails the ill-posed problem of retrieving a set of source signals observed through a mixing operator. Solving this problem requires prior knowledge, which is commonly incorporated by imposing regularity conditions on the source signals or implicitly learned in supervised or unsupervised methods from existing data. While data-driven methods have shown great promise in source separation, they are often dependent on large amounts of data, which rarely exists in planetary space missions. Considering this challenge, we propose an unsupervised source separation scheme for domains with limited data access that involves solving an optimization problem in the wavelet scattering representation space$\unicode{x2014}$an interpretable low-dimensional representation of stationary processes. We present a real-data example in which we remove transient thermally induced microtilts, known as glitches, from data recorded by a seismometer during NASA's InSight mission on Mars. Owing to the wavelet scattering covariances' ability to capture non-Gaussian properties of stochastic processes, we are able to separate glitches using only a few glitch-free data snippets.
Scale Dependencies and Self-Similarity Through Wavelet Scattering Covariance
Apr 19, 2022



Abstract:We introduce a scattering covariance matrix which provides non-Gaussian models of time-series having stationary increments. A complex wavelet transform computes signal variations at each scale. Dependencies across scales are captured by the joint covariance across time and scales of complex wavelet coefficients and their modulus. This covariance is nearly diagonalized by a second wavelet transform, which defines the scattering covariance. We show that this set of moments characterizes a wide range of non-Gaussian properties of multi-scale processes. This is analyzed for a variety of processes, including fractional Brownian motions, Poisson, multifractal random walks and Hawkes processes. We prove that self-similar processes have a scattering covariance matrix which is scale invariant. This property can be estimated numerically and defines a class of wide-sense self-similar processes. We build maximum entropy models conditioned by scattering covariance coefficients, and generate new time-series with a microcanonical sampling algorithm. Applications are shown for highly non-Gaussian financial and turbulence time-series.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge