MIMIC: A Generative Multimodal Foundation Model for Biomolecules

Biological function emerges from coupled constraints across sequence, structure, regulation, evolution, and cellular context, yet most foundation models in biology are trained within one modality or for a fixed forward task. We present MIMIC, a generative multimodal foundation model trained on our newly curated and aligned dataset, LORE, linking nucleic acid, protein, evolutionary, structural, regulatory, and semantic/contextual modalities within partially observed biomolecular states. MIMIC uses a split-track encoder-decoder architecture to condition on arbitrary subsets of observed modalities and reconstruct or generate missing components of molecular state across the genome, transcriptome, and proteome. Multimodal conditioning consistently improves MIMIC's sequence reconstruction relative to sequence-only inputs, while its learned representations enable state-of-the-art performance on RNA and protein downstream tasks. MIMIC achieves state-of-the-art splicing prediction, and its joint generative formulation enables isoform-aware inference that further improves performance. Beyond prediction, the same generative framework supports constrained design. For RNA, MIMIC identifies corrective edits in a clinically relevant HBB splice-disrupting mutation without reverting it by using evolutionary and structural signals. For proteins, jointly conditioning on shape and surface chemistry of PD-L1 and hACE2 binding sites produces diverse, high-confidence sequences with strong in silico support for target binding. Finally, MIMIC uses experimental context as semantic conditioning to model assay-dependent RNA chemical probing, rather than treating context as a fixed output. Together, these results position MIMIC's aligned multimodal generative modeling as a strong foundation for unifying representation learning, conditional prediction, and constrained biomolecular design within a single model.

Walrus: A Cross-Domain Foundation Model for Continuum Dynamics

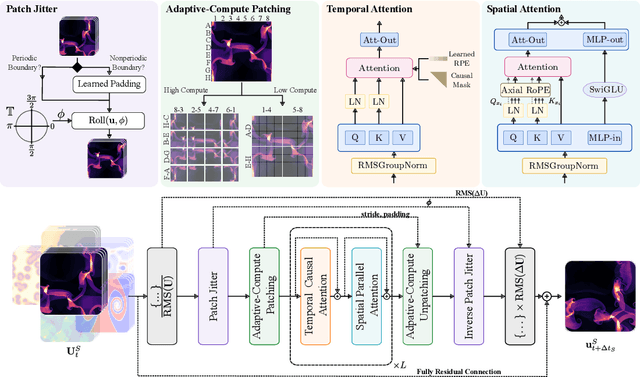
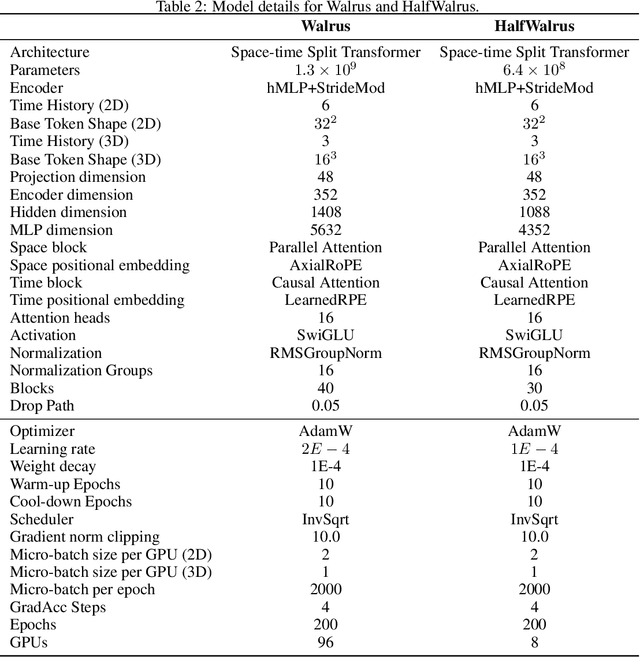
Foundation models have transformed machine learning for language and vision, but achieving comparable impact in physical simulation remains a challenge. Data heterogeneity and unstable long-term dynamics inhibit learning from sufficiently diverse dynamics, while varying resolutions and dimensionalities challenge efficient training on modern hardware. Through empirical and theoretical analysis, we incorporate new approaches to mitigate these obstacles, including a harmonic-analysis-based stabilization method, load-balanced distributed 2D and 3D training strategies, and compute-adaptive tokenization. Using these tools, we develop Walrus, a transformer-based foundation model developed primarily for fluid-like continuum dynamics. Walrus is pretrained on nineteen diverse scenarios spanning astrophysics, geoscience, rheology, plasma physics, acoustics, and classical fluids. Experiments show that Walrus outperforms prior foundation models on both short and long term prediction horizons on downstream tasks and across the breadth of pretraining data, while ablation studies confirm the value of our contributions to forecast stability, training throughput, and transfer performance over conventional approaches. Code and weights are released for community use.

Multimodal Datasets with Controllable Mutual Information

We introduce a framework for generating highly multimodal datasets with explicitly calculable mutual information between modalities. This enables the construction of benchmark datasets that provide a novel testbed for systematic studies of mutual information estimators and multimodal self-supervised learning techniques. Our framework constructs realistic datasets with known mutual information using a flow-based generative model and a structured causal framework for generating correlated latent variables.

What's In Your Field? Mapping Scientific Research with Knowledge Graphs and Large Language Models

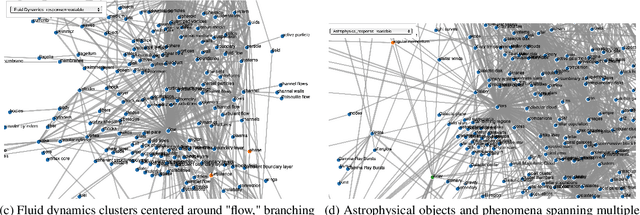
The scientific literature's exponential growth makes it increasingly challenging to navigate and synthesize knowledge across disciplines. Large language models (LLMs) are powerful tools for understanding scientific text, but they fail to capture detailed relationships across large bodies of work. Unstructured approaches, like retrieval augmented generation, can sift through such corpora to recall relevant facts; however, when millions of facts influence the answer, unstructured approaches become cost prohibitive. Structured representations offer a natural complement -- enabling systematic analysis across the whole corpus. Recent work enhances LLMs with unstructured or semistructured representations of scientific concepts; to complement this, we try extracting structured representations using LLMs. By combining LLMs' semantic understanding with a schema of scientific concepts, we prototype a system that answers precise questions about the literature as a whole. Our schema applies across scientific fields and we extract concepts from it using only 20 manually annotated abstracts. To demonstrate the system, we extract concepts from 30,000 papers on arXiv spanning astrophysics, fluid dynamics, and evolutionary biology. The resulting database highlights emerging trends and, by visualizing the knowledge graph, offers new ways to explore the ever-growing landscape of scientific knowledge. Demo: abby101/surveyor-0 on HF Spaces. Code: https://github.com/chiral-carbon/kg-for-science.

Dyads: Artist-Centric, AI-Generated Dance Duets

Existing AI-generated dance methods primarily train on motion capture data from solo dance performances, but a critical feature of dance in nearly any genre is the interaction of two or more bodies in space. Moreover, many works at the intersection of AI and dance fail to incorporate the ideas and needs of the artists themselves into their development process, yielding models that produce far more useful insights for the AI community than for the dance community. This work addresses both needs of the field by proposing an AI method to model the complex interactions between pairs of dancers and detailing how the technical methodology can be shaped by ongoing co-creation with the artistic stakeholders who curated the movement data. Our model is a probability-and-attention-based Variational Autoencoder that generates a choreographic partner conditioned on an input dance sequence. We construct a custom loss function to enhance the smoothness and coherence of the generated choreography. Our code is open-source, and we also document strategies for other interdisciplinary research teams to facilitate collaboration and strong communication between artists and technologists.

Invisible Strings: Revealing Latent Dancer-to-Dancer Interactions with Graph Neural Networks

Dancing in a duet often requires a heightened attunement to one's partner: their orientation in space, their momentum, and the forces they exert on you. Dance artists who work in partnered settings might have a strong embodied understanding in the moment of how their movements relate to their partner's, but typical documentation of dance fails to capture these varied and subtle relationships. Working closely with dance artists interested in deepening their understanding of partnering, we leverage Graph Neural Networks (GNNs) to highlight and interpret the intricate connections shared by two dancers. Using a video-to-3D-pose extraction pipeline, we extract 3D movements from curated videos of contemporary dance duets, apply a dedicated pre-processing to improve the reconstruction, and train a GNN to predict weighted connections between the dancers. By visualizing and interpreting the predicted relationships between the two movers, we demonstrate the potential for graph-based methods to construct alternate models of the collaborative dynamics of duets. Finally, we offer some example strategies for how to use these insights to inform a generative and co-creative studio practice.

Contextual Counting: A Mechanistic Study of Transformers on a Quantitative Task

Transformers have revolutionized machine learning across diverse domains, yet understanding their behavior remains crucial, particularly in high-stakes applications. This paper introduces the contextual counting task, a novel toy problem aimed at enhancing our understanding of Transformers in quantitative and scientific contexts. This task requires precise localization and computation within datasets, akin to object detection or region-based scientific analysis. We present theoretical and empirical analysis using both causal and non-causal Transformer architectures, investigating the influence of various positional encodings on performance and interpretability. In particular, we find that causal attention is much better suited for the task, and that no positional embeddings lead to the best accuracy, though rotary embeddings are competitive and easier to train. We also show that out of distribution performance is tightly linked to which tokens it uses as a bias term.

AstroCLIP: Cross-Modal Pre-Training for Astronomical Foundation Models

We present AstroCLIP, a strategy to facilitate the construction of astronomical foundation models that bridge the gap between diverse observational modalities. We demonstrate that a cross-modal contrastive learning approach between images and optical spectra of galaxies yields highly informative embeddings of both modalities. In particular, we apply our method on multi-band images and optical spectra from the Dark Energy Spectroscopic Instrument (DESI), and show that: (1) these embeddings are well-aligned between modalities and can be used for accurate cross-modal searches, and (2) these embeddings encode valuable physical information about the galaxies -- in particular redshift and stellar mass -- that can be used to achieve competitive zero- and few- shot predictions without further finetuning. Additionally, in the process of developing our approach, we also construct a novel, transformer-based model and pretraining approach for processing galaxy spectra.

Multiple Physics Pretraining for Physical Surrogate Models

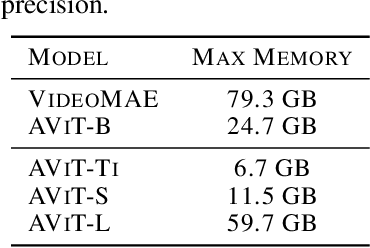
We introduce multiple physics pretraining (MPP), an autoregressive task-agnostic pretraining approach for physical surrogate modeling. MPP involves training large surrogate models to predict the dynamics of multiple heterogeneous physical systems simultaneously by learning features that are broadly useful across diverse physical tasks. In order to learn effectively in this setting, we introduce a shared embedding and normalization strategy that projects the fields of multiple systems into a single shared embedding space. We validate the efficacy of our approach on both pretraining and downstream tasks over a broad fluid mechanics-oriented benchmark. We show that a single MPP-pretrained transformer is able to match or outperform task-specific baselines on all pretraining sub-tasks without the need for finetuning. For downstream tasks, we demonstrate that finetuning MPP-trained models results in more accurate predictions across multiple time-steps on new physics compared to training from scratch or finetuning pretrained video foundation models. We open-source our code and model weights trained at multiple scales for reproducibility and community experimentation.

xVal: A Continuous Number Encoding for Large Language Models

Large Language Models have not yet been broadly adapted for the analysis of scientific datasets due in part to the unique difficulties of tokenizing numbers. We propose xVal, a numerical encoding scheme that represents any real number using just a single token. xVal represents a given real number by scaling a dedicated embedding vector by the number value. Combined with a modified number-inference approach, this strategy renders the model end-to-end continuous when considered as a map from the numbers of the input string to those of the output string. This leads to an inductive bias that is generally more suitable for applications in scientific domains. We empirically evaluate our proposal on a number of synthetic and real-world datasets. Compared with existing number encoding schemes, we find that xVal is more token-efficient and demonstrates improved generalization.