MIMIC: A Generative Multimodal Foundation Model for Biomolecules

Biological function emerges from coupled constraints across sequence, structure, regulation, evolution, and cellular context, yet most foundation models in biology are trained within one modality or for a fixed forward task. We present MIMIC, a generative multimodal foundation model trained on our newly curated and aligned dataset, LORE, linking nucleic acid, protein, evolutionary, structural, regulatory, and semantic/contextual modalities within partially observed biomolecular states. MIMIC uses a split-track encoder-decoder architecture to condition on arbitrary subsets of observed modalities and reconstruct or generate missing components of molecular state across the genome, transcriptome, and proteome. Multimodal conditioning consistently improves MIMIC's sequence reconstruction relative to sequence-only inputs, while its learned representations enable state-of-the-art performance on RNA and protein downstream tasks. MIMIC achieves state-of-the-art splicing prediction, and its joint generative formulation enables isoform-aware inference that further improves performance. Beyond prediction, the same generative framework supports constrained design. For RNA, MIMIC identifies corrective edits in a clinically relevant HBB splice-disrupting mutation without reverting it by using evolutionary and structural signals. For proteins, jointly conditioning on shape and surface chemistry of PD-L1 and hACE2 binding sites produces diverse, high-confidence sequences with strong in silico support for target binding. Finally, MIMIC uses experimental context as semantic conditioning to model assay-dependent RNA chemical probing, rather than treating context as a fixed output. Together, these results position MIMIC's aligned multimodal generative modeling as a strong foundation for unifying representation learning, conditional prediction, and constrained biomolecular design within a single model.

Representation Learning for Spatiotemporal Physical Systems

Machine learning approaches to spatiotemporal physical systems have primarily focused on next-frame prediction, with the goal of learning an accurate emulator for the system's evolution in time. However, these emulators are computationally expensive to train and are subject to performance pitfalls, such as compounding errors during autoregressive rollout. In this work, we take a different perspective and look at scientific tasks further downstream of predicting the next frame, such as estimation of a system's governing physical parameters. Accuracy on these tasks offers a uniquely quantifiable glimpse into the physical relevance of the representations of these models. We evaluate the effectiveness of general-purpose self-supervised methods in learning physics-grounded representations that are useful for downstream scientific tasks. Surprisingly, we find that not all methods designed for physical modeling outperform generic self-supervised learning methods on these tasks, and methods that learn in the latent space (e.g., joint embedding predictive architectures, or JEPAs) outperform those optimizing pixel-level prediction objectives. Code is available at https://github.com/helenqu/physical-representation-learning.

Walrus: A Cross-Domain Foundation Model for Continuum Dynamics

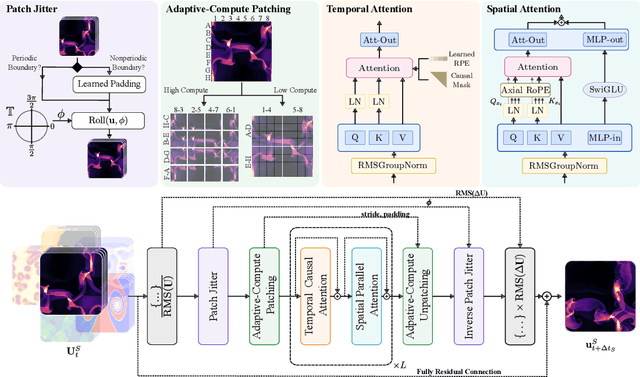
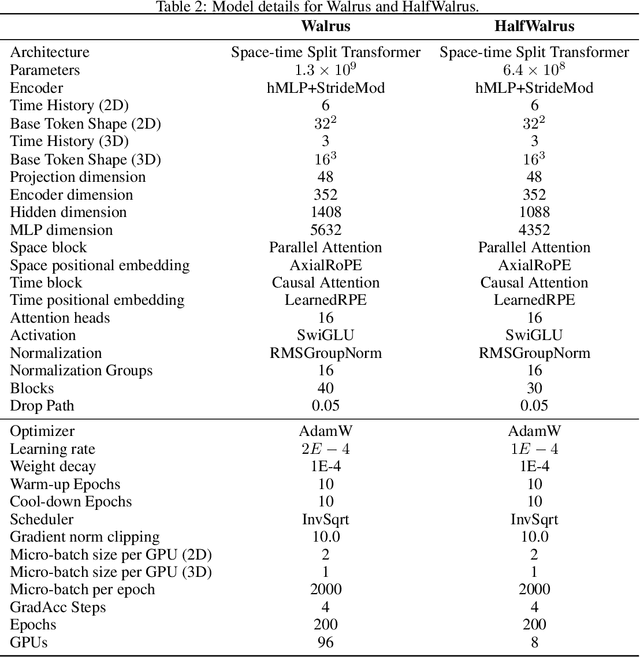
Foundation models have transformed machine learning for language and vision, but achieving comparable impact in physical simulation remains a challenge. Data heterogeneity and unstable long-term dynamics inhibit learning from sufficiently diverse dynamics, while varying resolutions and dimensionalities challenge efficient training on modern hardware. Through empirical and theoretical analysis, we incorporate new approaches to mitigate these obstacles, including a harmonic-analysis-based stabilization method, load-balanced distributed 2D and 3D training strategies, and compute-adaptive tokenization. Using these tools, we develop Walrus, a transformer-based foundation model developed primarily for fluid-like continuum dynamics. Walrus is pretrained on nineteen diverse scenarios spanning astrophysics, geoscience, rheology, plasma physics, acoustics, and classical fluids. Experiments show that Walrus outperforms prior foundation models on both short and long term prediction horizons on downstream tasks and across the breadth of pretraining data, while ablation studies confirm the value of our contributions to forecast stability, training throughput, and transfer performance over conventional approaches. Code and weights are released for community use.

Lost in Latent Space: An Empirical Study of Latent Diffusion Models for Physics Emulation

The steep computational cost of diffusion models at inference hinders their use as fast physics emulators. In the context of image and video generation, this computational drawback has been addressed by generating in the latent space of an autoencoder instead of the pixel space. In this work, we investigate whether a similar strategy can be effectively applied to the emulation of dynamical systems and at what cost. We find that the accuracy of latent-space emulation is surprisingly robust to a wide range of compression rates (up to 1000x). We also show that diffusion-based emulators are consistently more accurate than non-generative counterparts and compensate for uncertainty in their predictions with greater diversity. Finally, we cover practical design choices, spanning from architectures to optimizers, that we found critical to train latent-space emulators.

The Well: a Large-Scale Collection of Diverse Physics Simulations for Machine Learning

Machine learning based surrogate models offer researchers powerful tools for accelerating simulation-based workflows. However, as standard datasets in this space often cover small classes of physical behavior, it can be difficult to evaluate the efficacy of new approaches. To address this gap, we introduce the Well: a large-scale collection of datasets containing numerical simulations of a wide variety of spatiotemporal physical systems. The Well draws from domain experts and numerical software developers to provide 15TB of data across 16 datasets covering diverse domains such as biological systems, fluid dynamics, acoustic scattering, as well as magneto-hydrodynamic simulations of extra-galactic fluids or supernova explosions. These datasets can be used individually or as part of a broader benchmark suite. To facilitate usage of the Well, we provide a unified PyTorch interface for training and evaluating models. We demonstrate the function of this library by introducing example baselines that highlight the new challenges posed by the complex dynamics of the Well. The code and data is available at https://github.com/PolymathicAI/the_well.

Contextual Counting: A Mechanistic Study of Transformers on a Quantitative Task

Transformers have revolutionized machine learning across diverse domains, yet understanding their behavior remains crucial, particularly in high-stakes applications. This paper introduces the contextual counting task, a novel toy problem aimed at enhancing our understanding of Transformers in quantitative and scientific contexts. This task requires precise localization and computation within datasets, akin to object detection or region-based scientific analysis. We present theoretical and empirical analysis using both causal and non-causal Transformer architectures, investigating the influence of various positional encodings on performance and interpretability. In particular, we find that causal attention is much better suited for the task, and that no positional embeddings lead to the best accuracy, though rotary embeddings are competitive and easier to train. We also show that out of distribution performance is tightly linked to which tokens it uses as a bias term.

Multiple Physics Pretraining for Physical Surrogate Models

We introduce multiple physics pretraining (MPP), an autoregressive task-agnostic pretraining approach for physical surrogate modeling. MPP involves training large surrogate models to predict the dynamics of multiple heterogeneous physical systems simultaneously by learning features that are broadly useful across diverse physical tasks. In order to learn effectively in this setting, we introduce a shared embedding and normalization strategy that projects the fields of multiple systems into a single shared embedding space. We validate the efficacy of our approach on both pretraining and downstream tasks over a broad fluid mechanics-oriented benchmark. We show that a single MPP-pretrained transformer is able to match or outperform task-specific baselines on all pretraining sub-tasks without the need for finetuning. For downstream tasks, we demonstrate that finetuning MPP-trained models results in more accurate predictions across multiple time-steps on new physics compared to training from scratch or finetuning pretrained video foundation models. We open-source our code and model weights trained at multiple scales for reproducibility and community experimentation.

AstroCLIP: Cross-Modal Pre-Training for Astronomical Foundation Models

We present AstroCLIP, a strategy to facilitate the construction of astronomical foundation models that bridge the gap between diverse observational modalities. We demonstrate that a cross-modal contrastive learning approach between images and optical spectra of galaxies yields highly informative embeddings of both modalities. In particular, we apply our method on multi-band images and optical spectra from the Dark Energy Spectroscopic Instrument (DESI), and show that: (1) these embeddings are well-aligned between modalities and can be used for accurate cross-modal searches, and (2) these embeddings encode valuable physical information about the galaxies -- in particular redshift and stellar mass -- that can be used to achieve competitive zero- and few- shot predictions without further finetuning. Additionally, in the process of developing our approach, we also construct a novel, transformer-based model and pretraining approach for processing galaxy spectra.

xVal: A Continuous Number Encoding for Large Language Models

Large Language Models have not yet been broadly adapted for the analysis of scientific datasets due in part to the unique difficulties of tokenizing numbers. We propose xVal, a numerical encoding scheme that represents any real number using just a single token. xVal represents a given real number by scaling a dedicated embedding vector by the number value. Combined with a modified number-inference approach, this strategy renders the model end-to-end continuous when considered as a map from the numbers of the input string to those of the output string. This leads to an inductive bias that is generally more suitable for applications in scientific domains. We empirically evaluate our proposal on a number of synthetic and real-world datasets. Compared with existing number encoding schemes, we find that xVal is more token-efficient and demonstrates improved generalization.

Towards Stability of Autoregressive Neural Operators

Neural operators have proven to be a promising approach for modeling spatiotemporal systems in the physical sciences. However, training these models for large systems can be quite challenging as they incur significant computational and memory expense -- these systems are often forced to rely on autoregressive time-stepping of the neural network to predict future temporal states. While this is effective in managing costs, it can lead to uncontrolled error growth over time and eventual instability. We analyze the sources of this autoregressive error growth using prototypical neural operator models for physical systems and explore ways to mitigate it. We introduce architectural and application-specific improvements that allow for careful control of instability-inducing operations within these models without inflating the compute/memory expense. We present results on several scientific systems that include Navier-Stokes fluid flow, rotating shallow water, and a high-resolution global weather forecasting system. We demonstrate that applying our design principles to prototypical neural networks leads to significantly lower errors in long-range forecasts with 800\% longer forecasts without qualitative signs of divergence compared to the original models for these systems. We open-source our \href{https://anonymous.4open.science/r/stabilizing_neural_operators-5774/}{code} for reproducibility.