Representation Learning for Spatiotemporal Physical Systems

Machine learning approaches to spatiotemporal physical systems have primarily focused on next-frame prediction, with the goal of learning an accurate emulator for the system's evolution in time. However, these emulators are computationally expensive to train and are subject to performance pitfalls, such as compounding errors during autoregressive rollout. In this work, we take a different perspective and look at scientific tasks further downstream of predicting the next frame, such as estimation of a system's governing physical parameters. Accuracy on these tasks offers a uniquely quantifiable glimpse into the physical relevance of the representations of these models. We evaluate the effectiveness of general-purpose self-supervised methods in learning physics-grounded representations that are useful for downstream scientific tasks. Surprisingly, we find that not all methods designed for physical modeling outperform generic self-supervised learning methods on these tasks, and methods that learn in the latent space (e.g., joint embedding predictive architectures, or JEPAs) outperform those optimizing pixel-level prediction objectives. Code is available at https://github.com/helenqu/physical-representation-learning.

Opportunities in AI/ML for the Rubin LSST Dark Energy Science Collaboration

The Vera C. Rubin Observatory's Legacy Survey of Space and Time (LSST) will produce unprecedented volumes of heterogeneous astronomical data (images, catalogs, and alerts) that challenge traditional analysis pipelines. The LSST Dark Energy Science Collaboration (DESC) aims to derive robust constraints on dark energy and dark matter from these data, requiring methods that are statistically powerful, scalable, and operationally reliable. Artificial intelligence and machine learning (AI/ML) are already embedded across DESC science workflows, from photometric redshifts and transient classification to weak lensing inference and cosmological simulations. Yet their utility for precision cosmology hinges on trustworthy uncertainty quantification, robustness to covariate shift and model misspecification, and reproducible integration within scientific pipelines. This white paper surveys the current landscape of AI/ML across DESC's primary cosmological probes and cross-cutting analyses, revealing that the same core methodologies and fundamental challenges recur across disparate science cases. Since progress on these cross-cutting challenges would benefit multiple probes simultaneously, we identify key methodological research priorities, including Bayesian inference at scale, physics-informed methods, validation frameworks, and active learning for discovery. With an eye on emerging techniques, we also explore the potential of the latest foundation model methodologies and LLM-driven agentic AI systems to reshape DESC workflows, provided their deployment is coupled with rigorous evaluation and governance. Finally, we discuss critical software, computing, data infrastructure, and human capital requirements for the successful deployment of these new methodologies, and consider associated risks and opportunities for broader coordination with external actors.

Hybrid Physical-Neural Simulator for Fast Cosmological Hydrodynamics

Cosmological field-level inference requires differentiable forward models that solve the challenging dynamics of gas and dark matter under hydrodynamics and gravity. We propose a hybrid approach where gravitational forces are computed using a differentiable particle-mesh solver, while the hydrodynamics are parametrized by a neural network that maps local quantities to an effective pressure field. We demonstrate that our method improves upon alternative approaches, such as an Enthalpy Gradient Descent baseline, both at the field and summary-statistic level. The approach is furthermore highly data efficient, with a single reference simulation of cosmological structure formation being sufficient to constrain the neural pressure model. This opens the door for future applications where the model is fit directly to observational data, rather than a training set of simulations.

Lost in Latent Space: An Empirical Study of Latent Diffusion Models for Physics Emulation

The steep computational cost of diffusion models at inference hinders their use as fast physics emulators. In the context of image and video generation, this computational drawback has been addressed by generating in the latent space of an autoencoder instead of the pixel space. In this work, we investigate whether a similar strategy can be effectively applied to the emulation of dynamical systems and at what cost. We find that the accuracy of latent-space emulation is surprisingly robust to a wide range of compression rates (up to 1000x). We also show that diffusion-based emulators are consistently more accurate than non-generative counterparts and compensate for uncertainty in their predictions with greater diversity. Finally, we cover practical design choices, spanning from architectures to optimizers, that we found critical to train latent-space emulators.

Learning Diffusion Priors from Observations by Expectation Maximization

Diffusion models recently proved to be remarkable priors for Bayesian inverse problems. However, training these models typically requires access to large amounts of clean data, which could prove difficult in some settings. In this work, we present a novel method based on the expectation-maximization algorithm for training diffusion models from incomplete and noisy observations only. Unlike previous works, our method leads to proper diffusion models, which is crucial for downstream tasks. As part of our method, we propose and motivate a new posterior sampling scheme for unconditional diffusion models. We present empirical evidence supporting the effectiveness of our method.

Neural Posterior Estimation with Differentiable Simulators

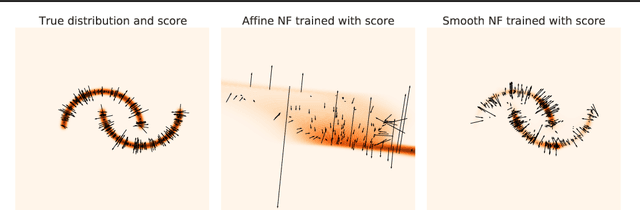
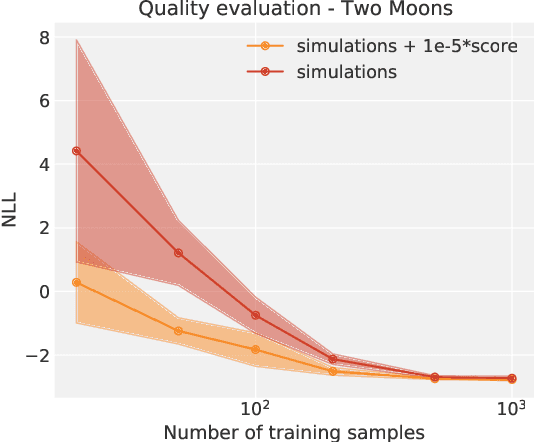
Simulation-Based Inference (SBI) is a promising Bayesian inference framework that alleviates the need for analytic likelihoods to estimate posterior distributions. Recent advances using neural density estimators in SBI algorithms have demonstrated the ability to achieve high-fidelity posteriors, at the expense of a large number of simulations ; which makes their application potentially very time-consuming when using complex physical simulations. In this work we focus on boosting the sample-efficiency of posterior density estimation using the gradients of the simulator. We present a new method to perform Neural Posterior Estimation (NPE) with a differentiable simulator. We demonstrate how gradient information helps constrain the shape of the posterior and improves sample-efficiency.

Hybrid Physical-Neural ODEs for Fast N-body Simulations

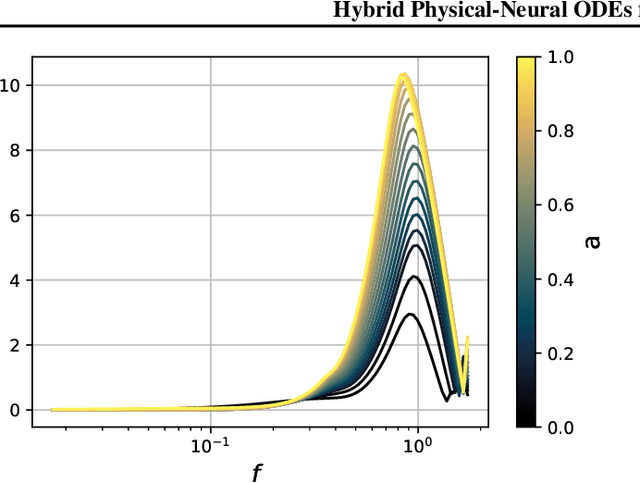
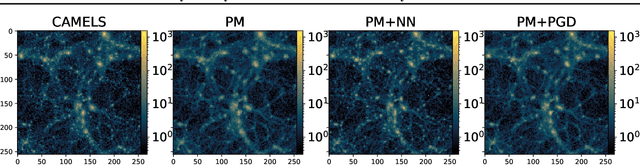
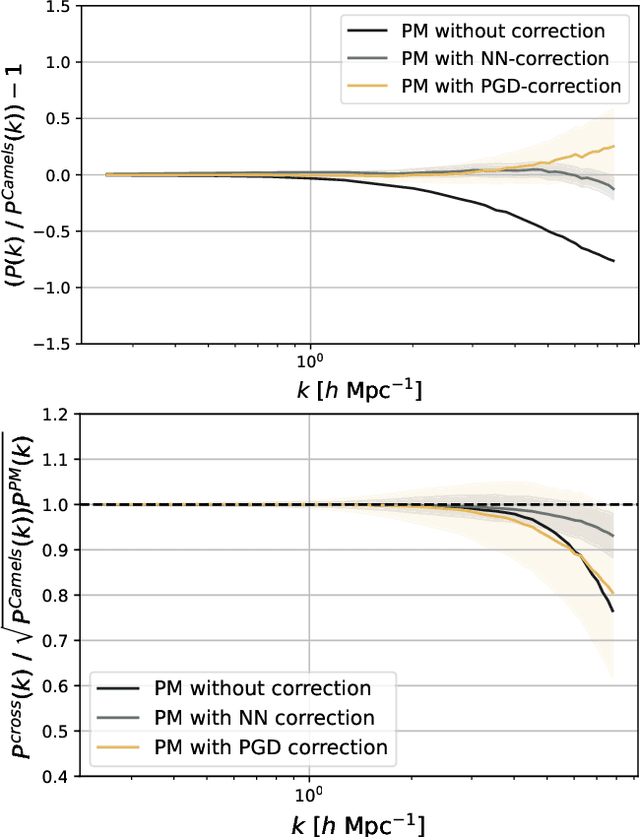
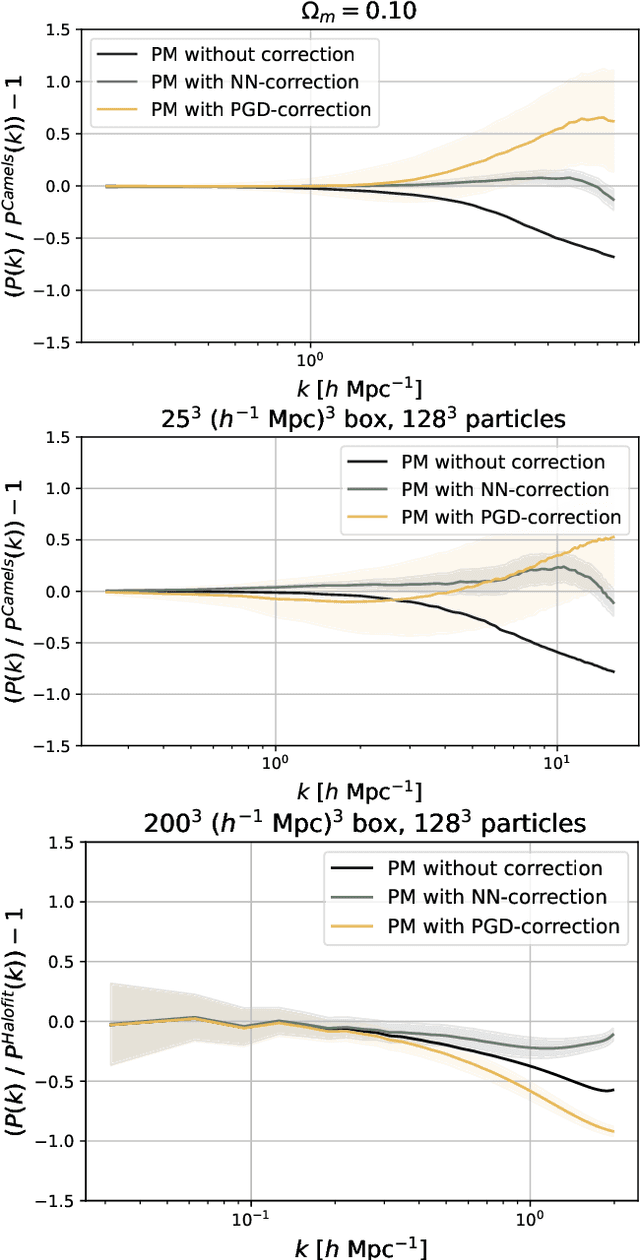
We present a new scheme to compensate for the small-scales approximations resulting from Particle-Mesh (PM) schemes for cosmological N-body simulations. This kind of simulations are fast and low computational cost realizations of the large scale structures, but lack resolution on small scales. To improve their accuracy, we introduce an additional effective force within the differential equations of the simulation, parameterized by a Fourier-space Neural Network acting on the PM-estimated gravitational potential. We compare the results for the matter power spectrum obtained to the ones obtained by the PGD scheme (Potential gradient descent scheme). We notice a similar improvement in term of power spectrum, but we find that our approach outperforms PGD for the cross-correlation coefficients, and is more robust to changes in simulation settings (different resolutions, different cosmologies).

Bayesian Neural Networks

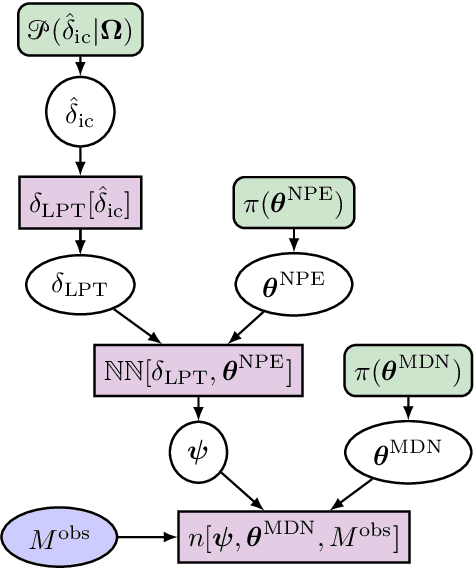
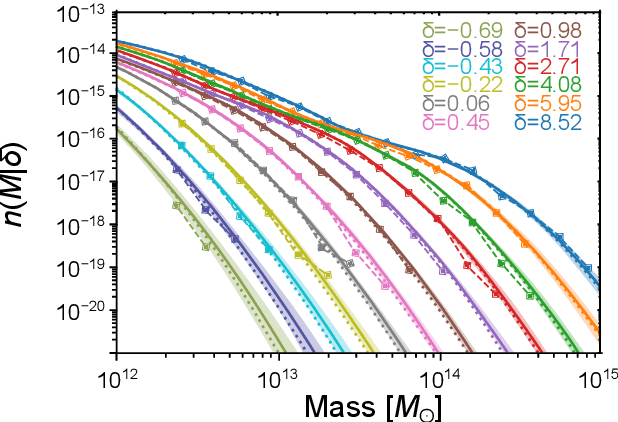
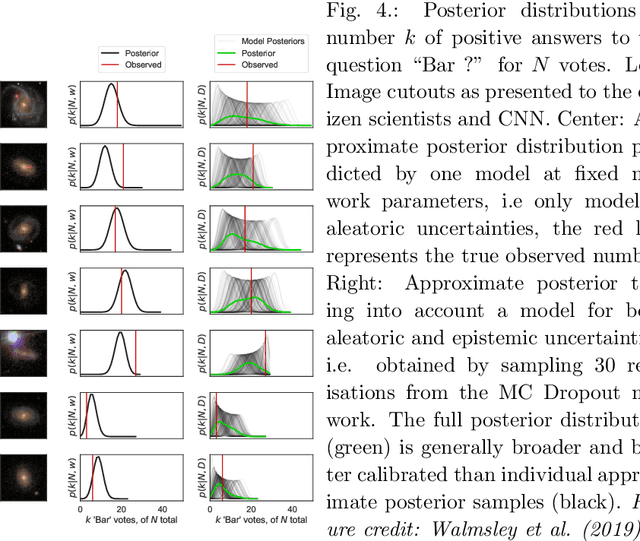
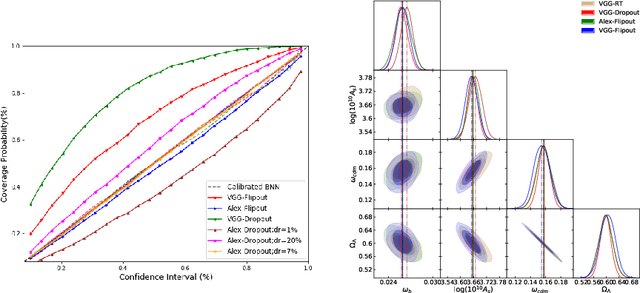
In recent times, neural networks have become a powerful tool for the analysis of complex and abstract data models. However, their introduction intrinsically increases our uncertainty about which features of the analysis are model-related and which are due to the neural network. This means that predictions by neural networks have biases which cannot be trivially distinguished from being due to the true nature of the creation and observation of data or not. In order to attempt to address such issues we discuss Bayesian neural networks: neural networks where the uncertainty due to the network can be characterised. In particular, we present the Bayesian statistical framework which allows us to categorise uncertainty in terms of the ingrained randomness of observing certain data and the uncertainty from our lack of knowledge about how data can be created and observed. In presenting such techniques we show how errors in prediction by neural networks can be obtained in principle, and provide the two favoured methods for characterising these errors. We will also describe how both of these methods have substantial pitfalls when put into practice, highlighting the need for other statistical techniques to truly be able to do inference when using neural networks.

Uncertainty Quantification with Generative Models

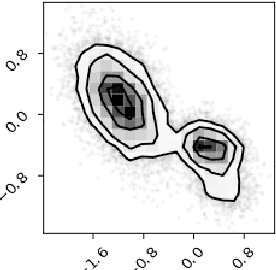
We develop a generative model-based approach to Bayesian inverse problems, such as image reconstruction from noisy and incomplete images. Our framework addresses two common challenges of Bayesian reconstructions: 1) It makes use of complex, data-driven priors that comprise all available information about the uncorrupted data distribution. 2) It enables computationally tractable uncertainty quantification in the form of posterior analysis in latent and data space. The method is very efficient in that the generative model only has to be trained once on an uncorrupted data set, after that, the procedure can be used for arbitrary corruption types.