Persistent Sampling: Unleashing the Potential of Sequential Monte Carlo

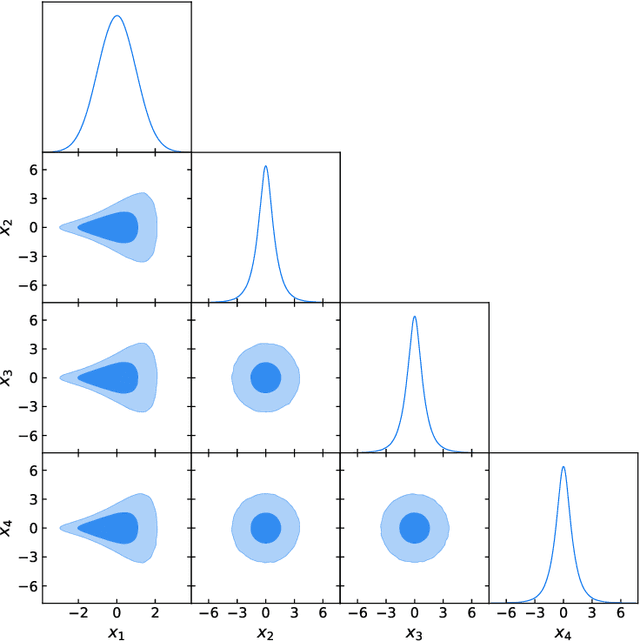
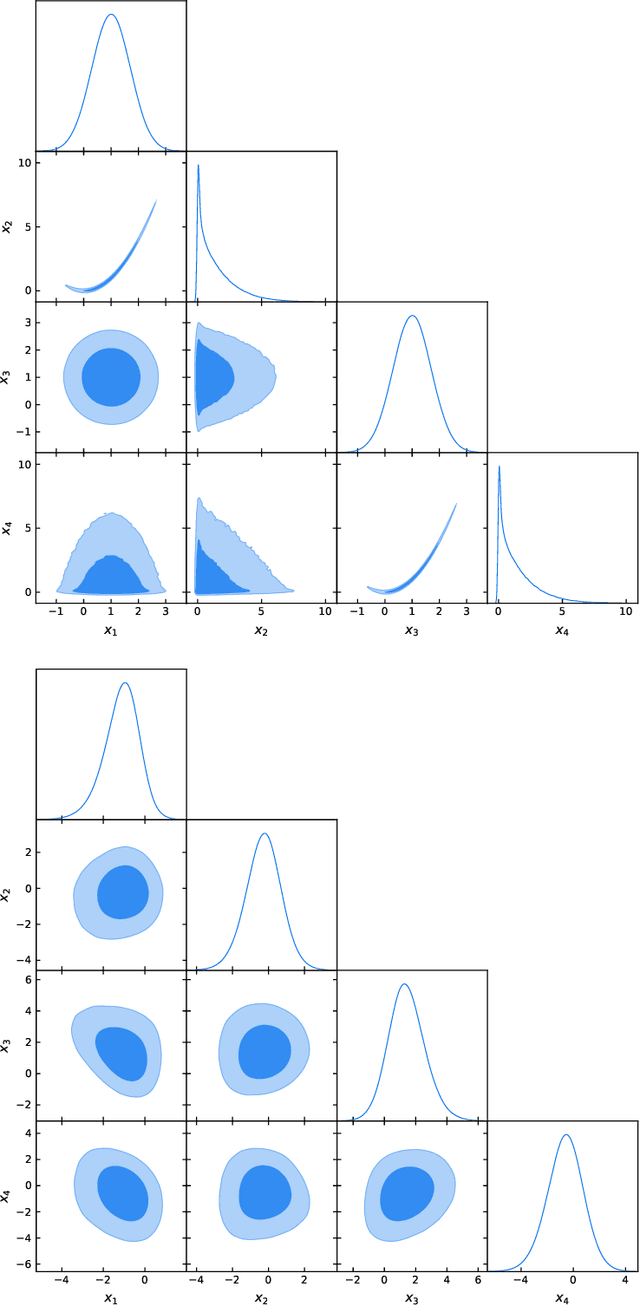
Sequential Monte Carlo (SMC) methods are powerful tools for Bayesian inference but suffer from requiring many particles for accurate estimates, leading to high computational costs. We introduce persistent sampling (PS), an extension of SMC that mitigates this issue by allowing particles from previous iterations to persist. This generates a growing, weighted ensemble of particles distributed across iterations. In each iteration, PS utilizes multiple importance sampling and resampling from the mixture of all previous distributions to produce the next generation of particles. This addresses particle impoverishment and mode collapse, resulting in more accurate posterior approximations. Furthermore, this approach provides lower-variance marginal likelihood estimates for model comparison. Additionally, the persistent particles improve transition kernel adaptation for efficient exploration. Experiments on complex distributions show that PS consistently outperforms standard methods, achieving lower squared bias in posterior moment estimation and significantly reduced marginal likelihood errors, all at a lower computational cost. PS offers a robust, efficient, and scalable framework for Bayesian inference.

Sequential Kalman Monte Carlo for gradient-free inference in Bayesian inverse problems

Ensemble Kalman Inversion (EKI) has been proposed as an efficient method for solving inverse problems with expensive forward models. However, the method is based on the assumption that we proceed through a sequence of Gaussian measures in moving from the prior to the posterior, and that the forward model is linear. In this work, we introduce Sequential Kalman Monte Carlo (SKMC) samplers, where we exploit EKI and Flow Annealed Kalman Inversion (FAKI) within a Sequential Monte Carlo (SMC) sampling scheme to perform efficient gradient-free inference in Bayesian inverse problems. FAKI employs normalizing flows (NF) to relax the Gaussian ansatz of the target measures in EKI. NFs are able to learn invertible maps between a Gaussian latent space and the original data space, allowing us to perform EKI updates in the Gaussianized NF latent space. However, FAKI alone is not able to correct for the model linearity assumptions in EKI. Errors in the particle distribution as we move through the sequence of target measures can therefore compound to give incorrect posterior moment estimates. In this work we consider the use of EKI and FAKI to initialize the particle distribution for each target in an adaptive SMC annealing scheme, before performing t-preconditioned Crank-Nicolson (tpCN) updates to distribute particles according to the target. We demonstrate the performance of these SKMC samplers on three challenging numerical benchmarks, showing significant improvements in the rate of convergence compared to standard SMC with importance weighted resampling at each temperature level. Code implementing the SKMC samplers is available at https://github.com/RichardGrumitt/KalmanMC.

Flow Annealed Kalman Inversion for Gradient-Free Inference in Bayesian Inverse Problems

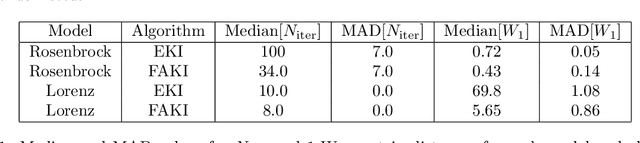
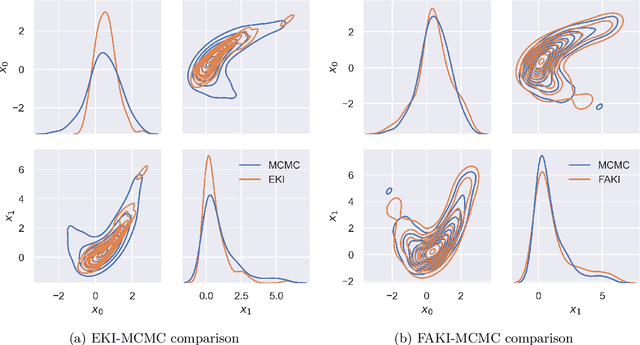
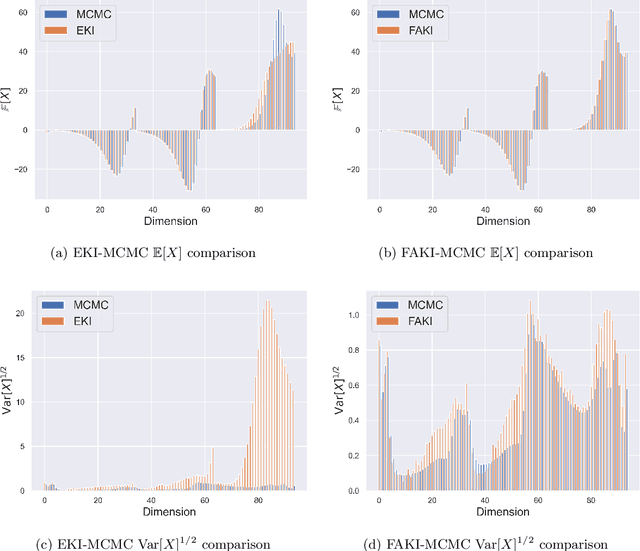
For many scientific inverse problems we are required to evaluate an expensive forward model. Moreover, the model is often given in such a form that it is unrealistic to access its gradients. In such a scenario, standard Markov Chain Monte Carlo algorithms quickly become impractical, requiring a large number of serial model evaluations to converge on the target distribution. In this paper we introduce Flow Annealed Kalman Inversion (FAKI). This is a generalization of Ensemble Kalman Inversion (EKI), where we embed the Kalman filter updates in a temperature annealing scheme, and use normalizing flows (NF) to map the intermediate measures corresponding to each temperature level to the standard Gaussian. In doing so, we relax the Gaussian ansatz for the intermediate measures used in standard EKI, allowing us to achieve higher fidelity approximations to non-Gaussian targets. We demonstrate the performance of FAKI on two numerical benchmarks, showing dramatic improvements over standard EKI in terms of accuracy whilst accelerating its already rapid convergence properties (typically in $\mathcal{O}(10)$ steps).

Microcanonical Langevin Monte Carlo

We propose a method for sampling from an arbitrary distribution $\exp[-S(\x)]$ with an available gradient $\nabla S(\x)$, formulated as an energy-preserving stochastic differential equation (SDE). We derive the Fokker-Planck equation and show that both the deterministic drift and the stochastic diffusion separately preserve the stationary distribution. This implies that the drift-diffusion discretization schemes are bias-free, in contrast to the standard Langevin dynamics. We apply the method to the $\phi^4$ lattice field theory, showing the results agree with the standard sampling methods but with significantly higher efficiency compared to the current state-of-the-art samplers.

Probabilistic Auto-Encoder

We introduce the Probabilistic Auto-Encoder (PAE), a generative model with a lower dimensional latent space that is based on an Auto-Encoder which is interpreted probabilistically after training using a Normalizing Flow. The PAE combines the advantages of an Auto-Encoder, i.e. it is fast and easy to train and achieves small reconstruction error, with the desired properties of a generative model, such as high sample quality and good performance in downstream tasks. Compared to a VAE and its common variants, the PAE trains faster, reaches lower reconstruction error and achieves state of the art samples without parameter fine-tuning or annealing schemes. We demonstrate that the PAE is further a powerful model for performing the downstream tasks of outlier detection and probabilistic image reconstruction: 1) Starting from the Laplace approximation to the marginal likelihood, we identify a PAE-based outlier detection metric which achieves state of the art results in Out-of-Distribution detection outperforming other likelihood based estimators. 2) Using posterior analysis in the PAE latent space we perform high dimensional data inpainting and denoising with uncertainty quantification.

Normalizing Constant Estimation with Gaussianized Bridge Sampling

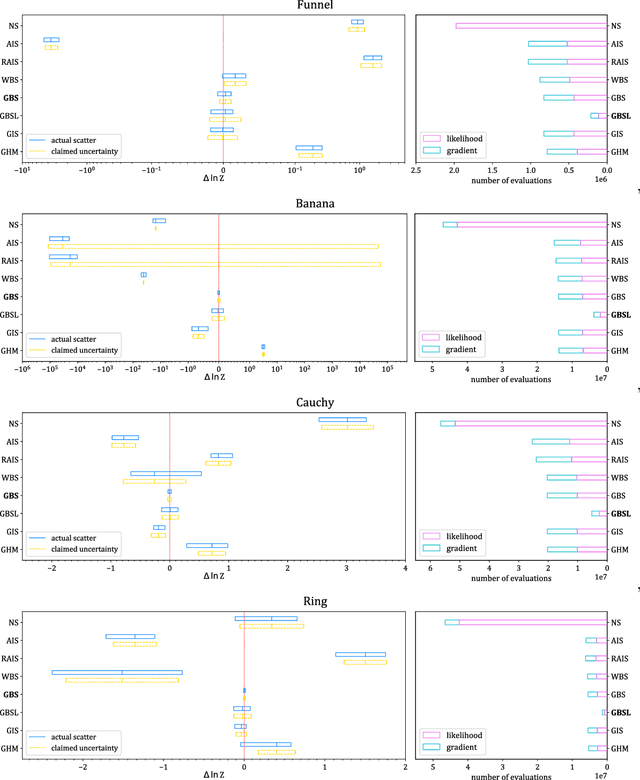
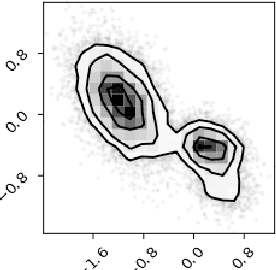
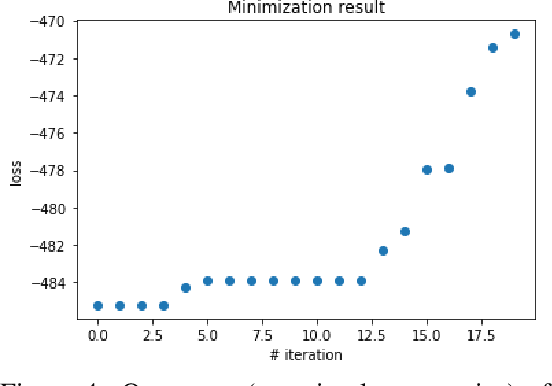
Normalizing constant (also called partition function, Bayesian evidence, or marginal likelihood) is one of the central goals of Bayesian inference, yet most of the existing methods are both expensive and inaccurate. Here we develop a new approach, starting from posterior samples obtained with a standard Markov Chain Monte Carlo (MCMC). We apply a novel Normalizing Flow (NF) approach to obtain an analytic density estimator from these samples, followed by Optimal Bridge Sampling (OBS) to obtain the normalizing constant. We compare our method which we call Gaussianized Bridge Sampling (GBS) to existing methods such as Nested Sampling (NS) and Annealed Importance Sampling (AIS) on several examples, showing our method is both significantly faster and substantially more accurate than these methods, and comes with a reliable error estimation.

Uncertainty Quantification with Generative Models

We develop a generative model-based approach to Bayesian inverse problems, such as image reconstruction from noisy and incomplete images. Our framework addresses two common challenges of Bayesian reconstructions: 1) It makes use of complex, data-driven priors that comprise all available information about the uncorrupted data distribution. 2) It enables computationally tractable uncertainty quantification in the form of posterior analysis in latent and data space. The method is very efficient in that the generative model only has to be trained once on an uncorrupted data set, after that, the procedure can be used for arbitrary corruption types.