Normalizing Constant Estimation with Gaussianized Bridge Sampling
Paper and Code
Dec 12, 2019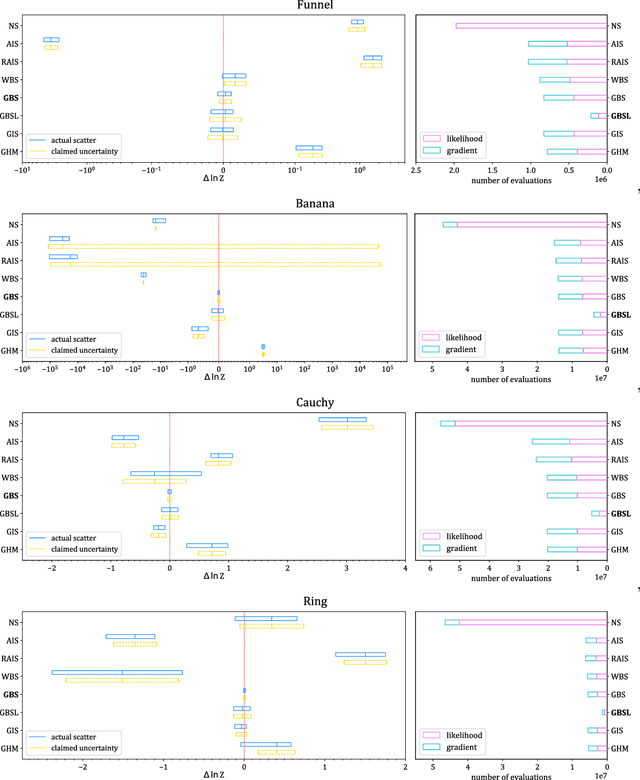

Normalizing constant (also called partition function, Bayesian evidence, or marginal likelihood) is one of the central goals of Bayesian inference, yet most of the existing methods are both expensive and inaccurate. Here we develop a new approach, starting from posterior samples obtained with a standard Markov Chain Monte Carlo (MCMC). We apply a novel Normalizing Flow (NF) approach to obtain an analytic density estimator from these samples, followed by Optimal Bridge Sampling (OBS) to obtain the normalizing constant. We compare our method which we call Gaussianized Bridge Sampling (GBS) to existing methods such as Nested Sampling (NS) and Annealed Importance Sampling (AIS) on several examples, showing our method is both significantly faster and substantially more accurate than these methods, and comes with a reliable error estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge